What Is the Equation of a Straight Line?
An equation of straight line is the linear equation that expresses the relationship between the coordinate points on a straight line.
A straight line extends infinitely on both sides. It has an infinite number of points. The equation of a straight line can be expressed in a variety of ways, such as point-slope form, slope-intercept form, general form, standard form, and so on and indicates the line’s slope, x-intercept, and y-intercept.
Recommended Games
Equation of a Straight Line: Definition
The equation of a straight line is the linear equation that is satisfied by all the points on the line. It is the relation between the x-coordinate and y-coordinate of any point on the line.
Recommended Worksheets
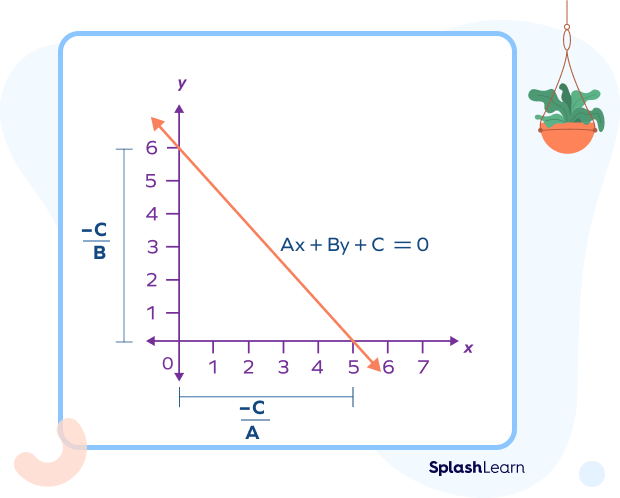
General Equation of a Line
The general equation of line is given by
$Ax + By + C = 0$
where A and B are not zero simultaneously.
A, B, and C are constants (real numbers).
When we graph this equation, we always get a straight line.
Note: A line represented by an equation in its general form $ax + by + c$, if $b \neq 0$ has slope $\frac{-a}{b}$ and y-intercept $\frac{-c}{b}$ .
Example: Consider the equation $x + 2y + 6 = 0$.
Here, $a = 1,\; b = 2,\; c = 6$
Slope of the line $= \;-\;\frac{a}{b} = \;-\;\frac{1}{2}$
y-intercept of the line $= \;-\;\frac{c}{b} = \;-\;\frac{6}{2} = \;-\;3$
Different Forms of Equation of a Straight Line
The equation of a straight line can be written in different forms, such as point-slope form, slope-intercept form, standard form, etc.
These forms help us understand how to find the equation of a straight line with the given information. Let’s discuss each form in detail.

Standard Form of Equation of Straight Line
The standard form of equation of a line is given by
$Ax + By = C$
where
A, B, and C are constants (integers),
and the values of A and B cannot be zero at the same time.
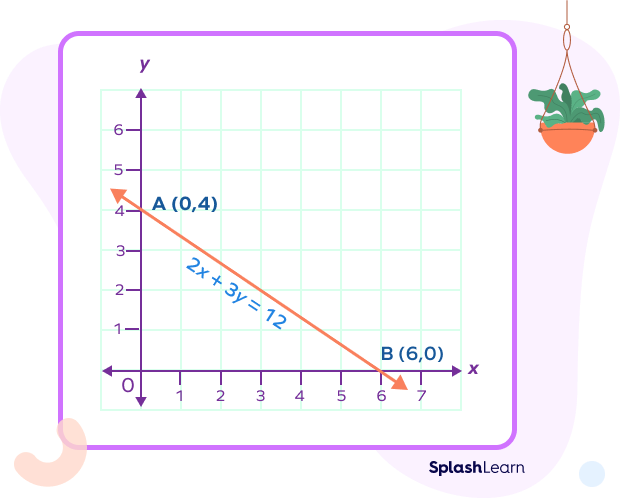
Example: Consider an equation $2x + 3y = 12$.
If we set $x = 0$,we get $3y = 12$ and we can find that $y = 4$, which means the y-intercept is (0,4).
In a similar way, we can set $y = 0$ to get $2x = 12$ and find that the x-intercept is (6,0).
Now we can graph the line:
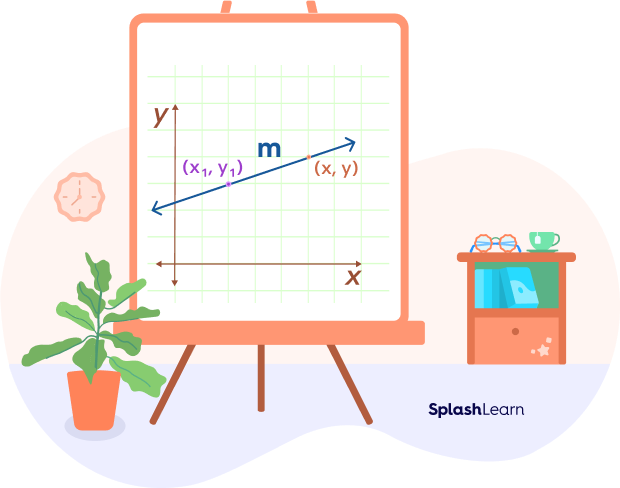
Point-Slope Form Equation of Straight Line
The point-slope form is used to determine the equation of a straight line passing through a point having coordinates $(x_{1},\; y_{1})$ and having slope m.
The point-slope form is given by
$y \;-\; y_{1} = m (x \;-\;x_{1})$
where $(x,\; y)$ is an arbitrary point on the line.
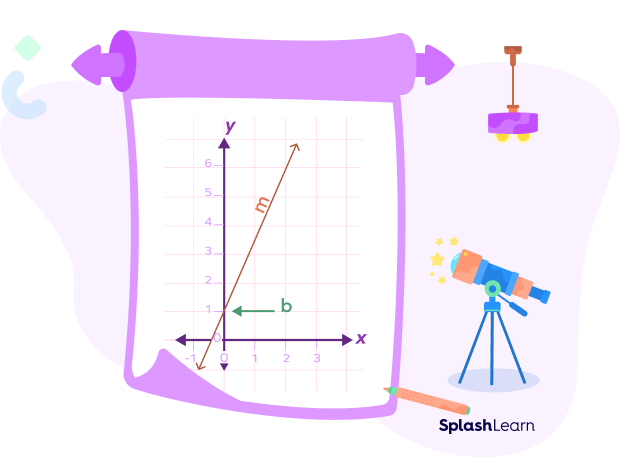
Slope-Intercept Form Equation of Straight Line
Suppose that a line has slope m and y-intercept b.
Thus, the line passes through the point (0, b).
Using the point-slope form, we can write
$y \;-\; b = m(x \;-\; 0)$
$y = mx + b$
The slope-intercept form of a line is $y = mx + b$.
Two Point Form Equation of Straight Line
Let’s understand how to find the equation of a straight line from two points. Let the line passes through the points be $A(x_{1},\;y_{1})$ and $B(x_{2},\;y_{2})$. Let $P (x,\;y)$ be any point on the straight line.
Now, the slope of the line $AB = \frac{y_{1}\;-\; y_{2}}{x_{1} \;-\; x_{2}}$
The slope of the line $AP = \frac{y_{1}\;-\; y_{2}}{x_{1} \;-\; x_{2}}$
But the three points A, B and P are collinear.
Therefore, slope of the line AP $=$ slope of the line AB
$\frac{y \;-\; y_{1}}{x \;-\; x_{1}} = \frac{y_{1}\;-\; y_{2}}{x_{1}\;-\; x_{2}}$
$(y\;-\; y_{1}) = \frac{y_{2}\;-\; y_{1}}{x_{2} \;-\; x_{1}} (x \;-\; x_{1})$
Thus, the equation of a line passing through two points $(x_{1},\;y_{1})$ and $(x_{2},\;y_{2})$ is
$y\;-\;y_{1} = \frac{y_{2} \;-\; y_{1}}{x_{2}\;-\; x_{1}} (x \;-\; x_{1})$
The above equation is satisfied by the coordinates of any point lying on the line AB and hence, represents the equation of the straight line AB.
Intercept Form Equation of Straight Line
If a line cuts the x-axis and y-axis at (a, 0) and (0, b), respectively, we say that the x-intercept is a and the y-intercept is b.
The equation of a straight line having x-intercept a and y-intercept b is given by
$(\frac{x}{a}) + (\frac{y}{b}) = 1$
Note: If a line is represented by an equation in its general form $ax + by + c$, and $c \neq 0$, then we have x-intercept $= \;-\;\frac{c}{a}$ and y-intercept $\;-\;\frac{c}{b}$ .
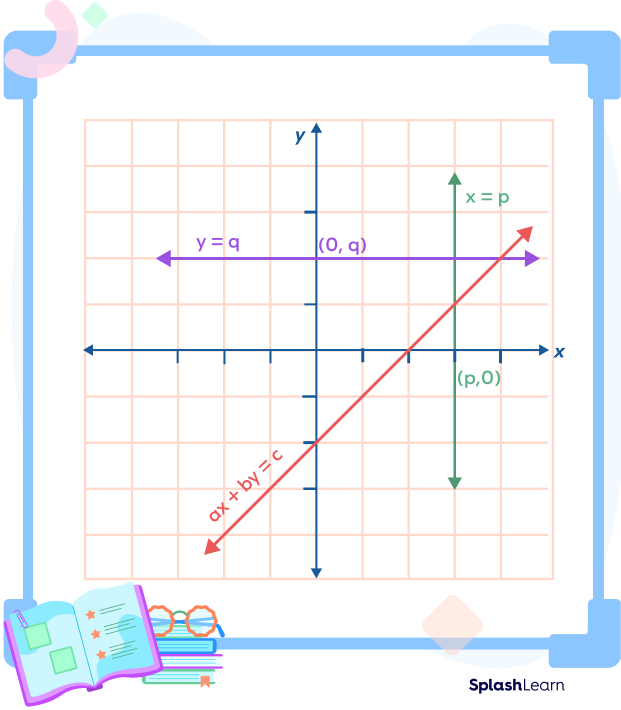
Graph of Different Equations of a Straight Line
The graph of an equation of a straight line in one variable y is a horizontal line parallel to the x-axis, and the graph of a linear equation in one variable x creates a vertical line parallel to the y-axis. A linear equation with two variables, x and y, generates a straight line on the graph.
Equation of a Straight Line Formulas
| General form | $Ax + By + C = 0$ |
| Standard form | $Ax + By = C$ |
| Equation of a horizontal line | $y = a (a \in R)$ |
| Equation of a vertical line | $x = b (b \in R)$ |
| Two point form | $y\;-\;y_{1} = \frac{y_{2} \;-\; y_{1}}{x_{2}\;-\; x_{1}} (x \;-\; x_{1})$ |
| Slope-intercept form | $y = mx + c$ |
| Intercept form | $(\frac{x}{a}) + (\frac{y}{b}) = 1$ |
Facts about Equation of a Straight Line
- The equation of x-axis is $y = 0$.
The equation of y-axis is $x = 0$. - The general form of a horizontal line is $y = b$.
The general form of a vertical line is $x = a$. - If two straight lines are parallel to each other, then they have the same slope.
- If two lines are perpendicular, the product of slopes is $\;-\;1$.
- In the general form of the equation of a straight line $ax + by + c, (b \neq 0)$, rearranging the terms, we get
by $= \;-\; ax \;-\; c$
$y = (\;-\;\frac{a}{b})x \;-\; (\frac{c}{b})$ …(1)
Slope-intercept form: $y = mx + c$ …(2)
By comparing (1) and (2), we get
Slope $= \;-\;\frac{a}{b}$ and y-intercept $= \;-\;\frac{c}{b}$ .
Conclusion
In this article, we learned about the equation of a straight line and its different forms. Let us solve some examples on the equation of a straight line to understand it better.
Solved Examples on Equation of a Straight Line
1. Find the slope and y-intercept of the line with equation $3x – 5y + 6 = 0$.
Solution:
The given equation of the line is $3x \;-\; 5y + 6 = 0$.
We need to convert this equation in the slope intercept form of the equation of a line.
$3x \;-\; 5y + 6 = 0$.
$3x + 6 = 5y$
$5y = 3x + 6$
$y = \frac{3x}{5} + \frac{6}{5}$
Comparing this equation with the slope-intercept form of the equation of line $y = mx + c$, we have
slope $m = \frac{3}{5}$
y-intercept $c = \frac{6}{5}$
2. Draw the graph of the linear equation $3x + 4y = 6$. At which points does the graph cut the x-axis and y-axis?
Solution:
Given equation is $3x + 4y = 6$.
Now, we need at least 2 points on the graph to draw this line.
(i) x-intercept
Substituting $y = 0$ in the equation, $3x + 4y = 6$, we get
$3x + (4 \times 0) = 6$
$3x = 6$
$x = 2$
Hence, the point at which the graph cuts x-axis $= (2,\; 0)$.
(ii) y-intercept
Substituting $x = 0$ in the equation, $3x + 4y = 6$, we get
$(3 \times 0) + 4y = 6$
$4y = 6$
$y = \frac{6}{4}$
$y = \frac{3}{2}$
$y = 1.5$
Hence, the point at which the graph cuts y-axis $= (0,\; 1.5)$.
Plotting the points (0, 1.5) and (2, 0) on the graph.

3. Find the equation of the straight line passing through the points with coordinates (3, 4) and $(6, \;-\;5)$.
Solution:
The equation of the straight line passing through the points (3, 4) and $(6, \;-\;5)$ is given by two-point form $\frac{y \;-\; y_{1}}{x \;-\; x_{1}} = \frac{y_{1}\;-\; y_{2}}{x_{1}\;-\; x_{2}}$.
$\frac{y \;-\; 4}{x \;-\; 3} = \frac{4 + 5}{3 \;-\; 6}$ (Using the form: $\frac{y \;-\; y_{1}}{x \;- \;x_{1}} = \frac{y_{1}\;-\; y_{2}}{x_{1}\;-\; x_{2}}$ )
$\frac{y \;-\; 4}{x \;-\; 3} = \frac{9}{\;-\;3}$
$\frac{y \;-\; 4}{x \;-\; 3} = \;-\;3$
$y \;-\; 4 = \;-\;3x + 9$
$3x + y = 13$ is the required equation.
4. Find the equation of a line passing through the point (6, 4) with a slope of 3.
Solution:
The equation of a line with slope m and one given point $(x_{1},\;y_{1})$ is $y\;-\; y_{1} = m (x\;-\; x_{1})$
The required equation of the line using this one point form is as follows
$(y\;-\;4) = 3(x\;-\;6)$
$(y\;-\;4) = 3x \;-\; 18$
$3x \;-\; 18 \;-\; y \;-\; 4 = 0$
$3x \;-\; y = 14$ is the required equation.
Practice Problems on Equation of a Straight Line
Equation of a Straight Line: Definition, Forms, Examples, Facts, FAQs
The slope of a line $ax + by + c = 0$, $(b \neq 0)$ is __________.
Rearranging the terms and comparing it with the slope-intercept form, we get
$y = (\;-\;\frac{a}{b})x \;-\; (\frac{c}{b})$
Thus, slope $= m = \;-\;\frac{a}{b}$
The slope-intercept form of a straight line is _________.
The slope-intercept form of a straight line is $y = mx + c$ , where m is the slope of the line and c is the y-intercept.
The equation of the x-axis is _______________.
Equation of the x-axis is $y = 0$.
The point-slope form is given by _______________.
The point-slope form is $y \;-\; y_{1} = m (x \;-\;x_{1})$, where (x, y) is an arbitrary point on the line.
The equation of the y-axis is _______________.
The equation of the y-axis is $x = 0$. The x-coordinate of any point on the y-axis is 0.
Frequently Asked Questions on Equation of a Straight Line
How do you write an equation for a vertical and horizontal line?
The equation of a horizontal line passing through (a, b) is of the form $y = b$. The equation of a vertical line passing through (a, b) is of the form $x = a$.
How to convert standard form to slope intercept form?
By rearrangement and comparison, we can change a line’s equation from standard form to slope intercept form. We know that the standard form of the equation of a straight line can be given as, $Ax + By + C = 0$. Rearranging the terms to find the value of “y,” we get,
$B \times y = \;-\;Ax \;-\; C$
$\Rightarrow y = (\;-\; \frac{A}{B})x + (\;-\; \frac{C}{B})$,where, $\;-\; AB$ makes the slope of the line and $(\;-\; \frac{C}{B})$ is the y-intercept.
What is c in the slope-intercept form of the equation of a line?
The “c” in the slope-intercept form of the equation of a line $y = mx + c$ is the y-intercept of the line. The line cuts the y-axis at the point (c, 0), and c is the distance of the point on the y-axis from the origin.
How can we find an equation of a line given the slope and a point?
To find an equation of a line given the slope and a point follow the following steps:
- Identify the slope and coordinates of the point.
- Substitute the values into the point-slope form, $y \;-\; y_{1} = m (x \;-\;x_{1})$.
- Write the equation in slope-intercept form.
What is the normal form of a straight line?
The normal form of the straight line is x cos $+$ y sin $=$ p.
Here, x and y are coordinates, p is the length of the perpendicular from origin to the straight line and is the angle between the positive x-axis and the perpendicular of the straight line from the origin.
The general form of the line $Ax + By + C = 0$ can be represented in normal form as:A cos $=$ B sin $= \;–\; p$