Exponent Formulas –  Examples, Facts, Practice Problems, FAQs

What Are Exponent Formulas?

The exponent formulas are mathematical rules that help you perform calculations and simplify expressions involving exponents more easily. 

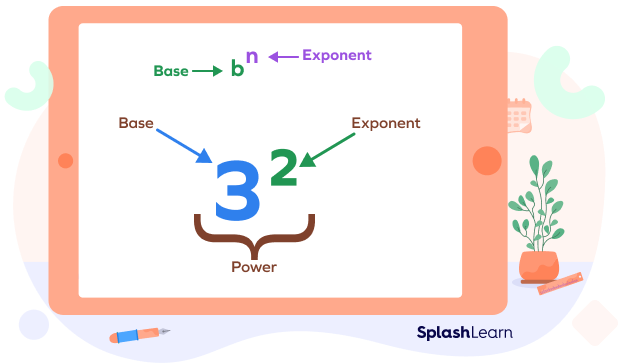
The exponent formulas represent the way to express a number raised to a certain power. It is written as Base^Exponent and signifies multiplying the base by itself the number of times indicated by the exponent.

Base and Exponent: The base of an exponent is the number or letter you want to multiply, and the exponent tells you how many times to multiply it by itself.

If you multiply the number “a” by itself n times, you can express this multiplication in a concise form using exponents, instead of writing the number over and over again.

Example: Multiply 5 by itself three times. 

Instead of writing $5 \times 5 \times 5$, we can write 5³. 

So, 5 raised to the power of 3 means you’re multiplying 5 by itself three times: $5 \times 5 \times 5$, which equals 125.

Here, 

5 is called the “base.“

3 is called the “exponent” or “power.“

5³ is read as “5 to the power of 3” (or) “5 raised to 3.” 

The entire expression is called power.

Exponent formulas simplify calculations with repeated multiplication. They involve rules like product, quotient, power of a power, and fractional exponents, vital for various mathematical applications.

These formulas offer a methodical technique to deal with numbers, variables, and exponent-based equations. When dealing with repeated components, they assist you in avoiding the need to carry out multiple multiplications.

Exponent Formulas

These formulas help to simplify expressions involving exponents. They involve rules for combining, separating, and simplifying terms with exponents.

Take a look at the table given below to understand the various exponents formulas.

Rule	Description	Formula
Multiplication Rule (Product of Powers Rule)	When you multiply numbers with the same base, add their exponents, keeping the same base.	$a^{m} \times a^{n} = a^{m+n}$
Division Rule(Power of Quotient Rule)	When you divide numbers with the same base, subtract their exponents, keeping the same base.	$\frac{a^{m}}{a^{n}} = a^{m-n} (a \neq 0)$
Power of a Power Rule	If the base raised to a power is being raised to another power, then the two powers are multiplied keeping the same base.	$(a^{m})^{n} = a^{mn}$
Power of a Product Rule	To find the power of a product, find the power of each factor and then multiply.	$(ab)^{m} = a^{m} \times b^{m}$
Power of a Fraction Rule	When you have a fraction ab raised to an exponent m, you can raise both the numerator (a) and the denominator (b) to the power (m).	$(\frac{a}{b})^{m} = \frac{a^{m}}{b^{m}} (b \neq 0)$
Zero Exponent	Any nonzero base raised to the power of 0 equals 1.	$a^{0} = 1$
Negative Exponent	Negative exponents indicate reciprocals. when a number is raised to a negative exponent, we divide 1 by the base raised to a positive exponent.	$a^{-m} = \frac{1}{a^{m}} (a \neq 0)$
Fractional Exponent	Exponents can also be fractional or rational numbers. The nth root of a number can be represented using fractional exponents.(a1nrepresents the nth root of a.)	$a^{\frac{m}{n}} = ^{n}\sqrt{a_{m}}$

Facts about Exponent Formulas

Conclusion

In this article, we learned about the exponent formulas. Exponents and powers formulas are essential tools in mathematics for simplifying and manipulating expressions involving powers and exponents. They provide a structured framework to work with numbers and variables raised to various powers. Now, let’s understand exponent formulas better using a few solved examples and practice problems.

Solved Examples on Exponent Formulas

Example 1: Simplify the following. 

a. $3^{4} \times 3^{2}$   

b. $\frac{x^{5}}{x^{3}}$   

c. $5^{0}$

Solution: 

a. $3^{4} \times 3^{2}$

Product of powers rule: $a^{m} \times a^{n} = a^{m+n}$

$3^{4} \times 3^{2} = 3^{4 + 2} = 3^{6} =729$

b. $\frac{x{5}}{x^{3}}$

Power of quotient rule: $\frac{a^{m}}{a^{n}} = a^{m-n}$

$\frac{x^{5}}{x^{3}} = x^{5-3} = x^{2}$

c. $5^{0}$

Zero exponent rule: $a^{0} = 1$

$5^{0} = 1$

Example 2: The dimensions of a rectangular box are $a^{4}$ inches, $b^{3}$ inches and a2 inches. Determine its volume.

Solution: 

length (l) $= a^{4}$ inches

width (w) $= b^{3}$ inches

height (h) $= a^{2}$ inches

Using the product of powers rule exponent formula, axay=ax+y

Volume $= a^{4} \times a^{2} \times b^{3}$

Volume $= a^{6} \times b^{3}$

The volume of the box is $a^{6} \times b^{3}$.

Example 3: Simplify: $\frac{y^{- \frac{3}{4}}}{y^{\frac{1}{4}}}$

Solution: 

$\frac{y^{-\frac{3}{4}}{y^{\frac{1}{4}}}$

$= y^{- \frac{3}{4} -\frac{1}{4}}$

$= y^{\frac{-3-1}{4}}$

$= y^{-1}$

$= \frac{1}{y}$

Example 4: If $2^{2x} = 32$ and $3^{y} = 27$, find the value of x + y.

Solution: 

First equation: $2^{2x} = 32$

We can rewrite 32 as 2⁵

$2^{2x} = 2^{5}$

Since the bases are the same (both are 2), we can equate the exponents.

$2x = 5$

$x = \frac{5}{2}$

Second equation: $3^{y} = 27$

We can rewrite 27 as $3^{3}$.

$3^{y} = 3^{3}$

Again, we can equate the exponents since the base is equal.

$y = 3$

Now, let’s find x + y

$x + y = \frac{5}{2} + 3 = \frac{5 + 6}{2} = \frac{11}{2}$

Practice Problems on Exponent Formulas

Frequently Asked Questions about Exponent Formulas