What Is Fractions to Percents Conversion?
Fractions to percents conversion is the method of expressing a given fraction as a percentage.
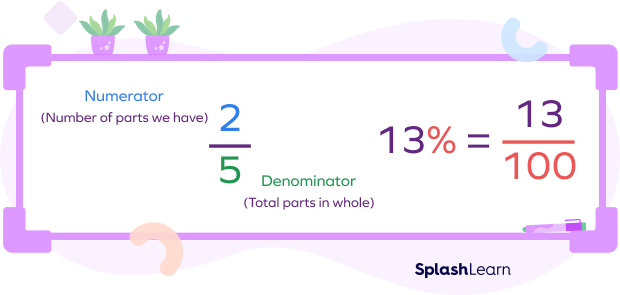
A fraction represents a part of the whole. A fraction $\frac{p}{q}$ consists of the numerator (p: top number) that represents the number of parts taken and denominator (q: bottom number), which represents the total number of parts the whole is divided into. For example, $\frac{2}{5}$ means 2 parts taken out of 5 equal parts.
A percentage is a fraction expressed as a fraction with a denominator of 100. In other words, percentage means a part per hundred. By “per cent” we mean “per 100.” Percent is represented by the symbol “$\%$.”
Converting fractions to percentages helps in comparing and ordering two quantities easily. Fractions, decimals, and percentages are all interrelated concepts. To convert a fraction to a percent, we can first convert it into a decimal. Multiply the given decimal by 100 to get the percentage value.

Recommended Games
How to Convert a Fraction to a Percent
To convert a fraction to a percent, simply convert fraction to decimal, multiply the decimal by 100, and add $\%$ sign. Another way to convert a fraction to a percentage is multiplying the fraction by 100, simplifying it, and adding$\%$ sign.
Step 1: Convert the fraction into a decimal number. To do this, divide the numerator by the denominator.
Step 2: To get a percent value, multiply the obtained decimal number by 100. The result is the fraction as a percent. Write the percent with $\%$ symbol next to the answer.

Another way is to multiply the fraction by 100 and simplify. The result is the fraction as a percent. Add the $\%$ symbol to the answer.
$\frac{4}{7} = (\frac{4}{7} \times 100)\% = \frac{400}{7}\% = 57.1428…\%$
Recommended Worksheets
Fraction to Percentage Formula
To convert a fraction to percent, we convert it to a decimal number and multiply it by 100 followed by the symbol $\%$.
The formula to convert fraction mn to percentage is:
Percentage $= \frac{m}{n}\times100$
where, $m =$ numerator
$n =$ denominator
Do not forget to add the “$\%$” sign after the final answer.

Fraction to Percent Conversion Table
Take a look at the fractions to percent conversion chart.
| Fraction | Percentage |
|---|---|
| $\frac{1}{2}$ | $50\%$ |
| $\frac{1}{4}$ | $25\%$ |
| $\frac{2}{5}$ | $40\%$ |
| $\frac{3}{4}$ | $75\%$ |
| $\frac{1}{5}$ | $20\%$ |
| $\frac{3}{5}$ | $60\%$ |
| $\frac{1}{8}$ | $12.5\%$ |
| $\frac{1}{10}$ | $10\%$ |
| $\frac{3}{10}$ | $30\%$ |
| $\frac{9}{10}$ | $90\%$ |
Facts about Fractions to Percent Conversion
- Fractions can be expressed as decimals by dividing the numerator (top number) by the denominator (bottom number) using the long division method.
- To change a fraction to a percentage, divide the numerator by the denominator, and then multiply the result by 100. Alternatively, you can also multiply the numerator by 100 first, then divide the result by the denominator of the fraction.
- You can convert a fraction to percent by making the denominator 100, or by converting
the fraction into $\frac{?}{100}$ form.
$\frac{4}{5} = \frac{4 \times 20}{5 \times 20} = \frac{80}{100} = 80\%$ - A mixed fraction or a mixed number is always greater than (or equal to) 1. Thus, we always get a percent greater than 100 on converting a mixed number to a percentage.
$2\frac{4}{5} = \frac{14}{5} = \frac{14}{5} \times 100= 280\%$ - To convert percent to fraction, remove the % sign, divide by 100, and simplify if required.
- $100\% = \frac{100}{100} = 1$
Conclusion
In this article, we have learned about fractions and percentages and their conversions. Conversion of fractions and decimals to percentages are very important. They make fractions and percentages of amounts much simpler to visualize and compare. Now, let’s apply the knowledge to solve some examples and practice problems.
Solved Examples on Converting Fractions to Percent
1. Convert each of the fractions to percentages.
- $\frac{3}{10}$ (b) $\frac{1}{4}$ (c) $\frac{1}{2}$
Solution:
To convert fractions to percentages, we can first convert it to a decimal form and then multiply it by 100.
(a) $\frac{3}{10}$
$\frac{3}{10} = 0.3$
Multiply it by 100 to get the percentage value.
$\frac{3}{10} = (0.3 \times 100)\% = 30\%$
(b) $\frac{1}{4} = (0.25 \times 100)\% = 25\%$
(c) $\frac{1}{2} = (0.50 \times 100)\% = 50\%$
2. Compare the fractions $\frac{3}{4}$ and $\frac{4}{5}$ by converting them into percentages.
Solution:
Let’s convert these fractions to percentages.
$\frac{3}{4} = (\frac{3}{4} \times 100)\% = (0.75 \times 100)\% = 75\%$
$\frac{4}{5} = (\frac{4}{5} \times 100)\% = (0.8 \times 100)\% = 80\%$
$75\% \lt 80\%$
Thus, $\frac{3}{4} \lt \frac{4}{5}$
3. Kids at a birthday party finished 6 out of 10 slices of pizza. What percentage of pizza was eaten by kids?
Solution:
6 out of $10 = \frac{6}{10}$
To change this fraction to percentage, we will multiply the fraction by 100.
$\frac{6}{10} = (\frac{6}{10} \times 100)\% = 60\%$
Thus, $60\%$ pizza was consumed.
4. Convert $\frac{3}{25}$ into a percentage.
Solution:
$\frac{3}{25} = (\frac{3}{25} \times 100)\%$
$\frac{3}{25} = \frac{300}{25}\%$
$\frac{3}{25} = 12\%$
Practice Problems on Fractions to Percent Conversion
Converting Fractions to Percent: Steps, Formula, Table, Examples, FAQs
Which option defines the gray shaded portion of the circle?
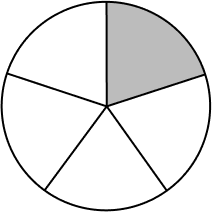
A circle is divided into 5 equal parts. One part is shaded. It represents the fraction $\frac{1}{5}$.
Thus, $\frac{1}{5} = (0.20 \times 100)\% = 20\%$
$\frac{3}{4}$ is equivalent to
$\frac{3}{4} \times 100 = 3 \times 25 = 75\%$
For converting fraction to percent, we __________.
For converting a decimal to percent, we multiply the fraction by 100, simplify, and give the $\%$ sign.
$22\%$ can be written as the following decimal and fraction.
$22\% = \frac{22}{100} = 0.22$
Convert the fraction to a percent: $\frac{7}{8}$
$\frac{7}{8} = \frac{7}{8} \times 100 = \frac{700}{8} = 87.5\%$
Frequently Asked Questions about Converting Fractions to Percent
Why do we need to convert a fraction to percent?
We need to convert a decimal to percent for comparing the quantities instantly. For example, if we have to compare the decimals of $\frac{1}{2},\; \frac{61}{100},\; \frac{987}{1000}$, we will not be able to make any sense of the values at first glance. If these fractions are converted into percentages as $50\%,\; 61\%,\; 98.7\%$, we will be able to compare them easily.
What are the steps to convert percent to fraction?
Step 1: Write down the given percent value like this: $\frac{Percent value}{100}$
Step 2: Simplify (or reduce) the fraction to its lowest term.
For example: Convert $20\%$ to fraction
$20\% = \frac{20}{100} = \frac{20}{100} \div \frac{20}{20} = \frac{1}{5}$
Thus, $20\% = \frac{1}{5}$
How do you convert a mixed number to a percentage?
To convert a mixed number to a percentage, first convert the mixed number to an improper fraction, and then convert the important fraction to a percentage.
$1\frac{2}{10} = \frac{12}{10} = \frac{12}{10} \times 100 = 120\%$
How do you convert an improper fraction to a percentage?
Divide the numerator by the denominator to get the decimal, and then multiply the decimal by 100.
Example: $\frac{7}{5} = 1.4$
$1.4 \times 100 = 140\%$




































