What Are Intersecting Lines?
When two or more lines cross or meet each other in a plane, the lines are called intersecting lines.
- Point of Intersection:
Intersecting lines share a common point called the point of intersection.
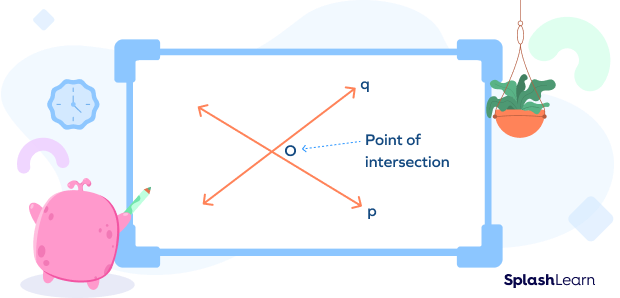
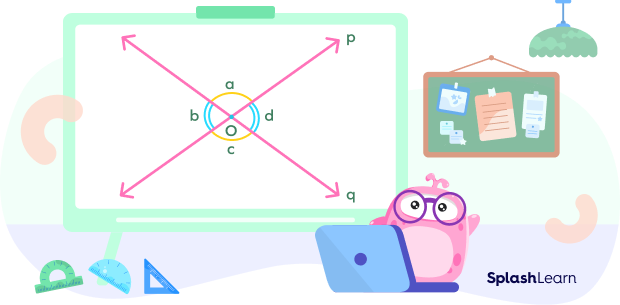
In the figure below, lines p and q intersect at point O. So, point O is the point of intersection.
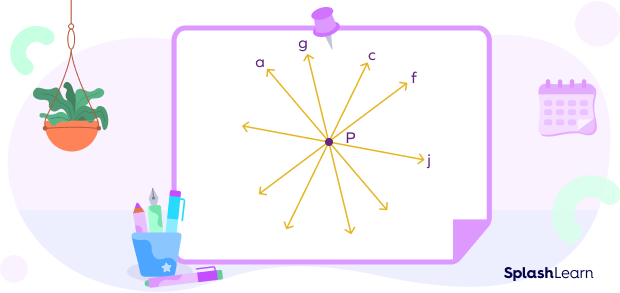
In the image below, many straight lines cross each other and intersect at the common point P. Here, P is called the point of concurrency.
Note: Three or more lines can share more than one point of intersection.
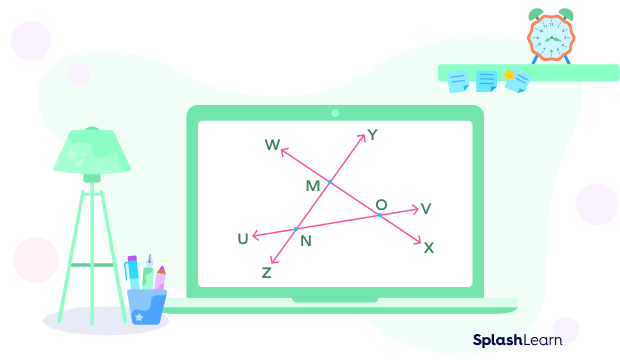
In the given diagram, there are three lines$\overset{\leftrightarrow}{WX}$, $\overset{\leftrightarrow}{YZ}$, and $\overset{\leftrightarrow}{UV}$ intersecting each other at three points, M, N, and O.
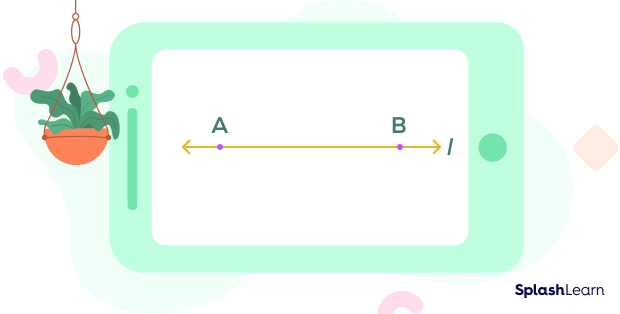
A line is a one-dimensional figure since it has only length and no width. It extends endlessly in both directions, and we cannot determine its length. One and only one line can pass through any two given points.
In the given diagram, the line is determined by two points, A and B. It can be written as line $\overset{\leftrightarrow}{AB}$ or simply as line l.
Recommended Games
Intersecting Lines Definition
Intersecting lines refer to two or more lines that cross or meet at a common point, which is known as the point of intersection.
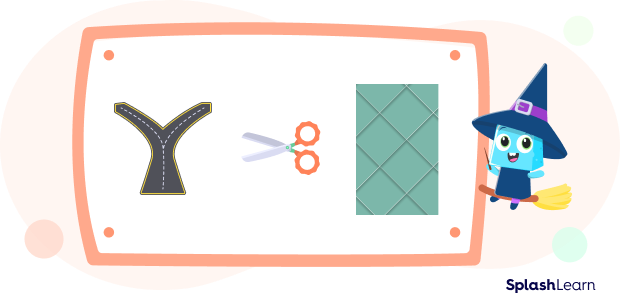
Real-life Examples of Intersecting Lines
- Scissors: The two arms of a pair of scissors
- Crossroads: Two roads (considered straight lines) meeting at a common point make crossroads.
- Patterns: The lines on the floor
- We use the word “intersection” in daily life in reference to roads or streets.
Example: Traffic at the intersection, taking a turn at the intersection, etc.
An intersection is the place where two or more streets, roads, or lines meet.

Angles Formed by Two Intersecting Lines
When two lines intersect each other, different types of angles are formed. The angles formed by the intersection of two lines are vertical angles, adjacent angles, linear pairs of angles.
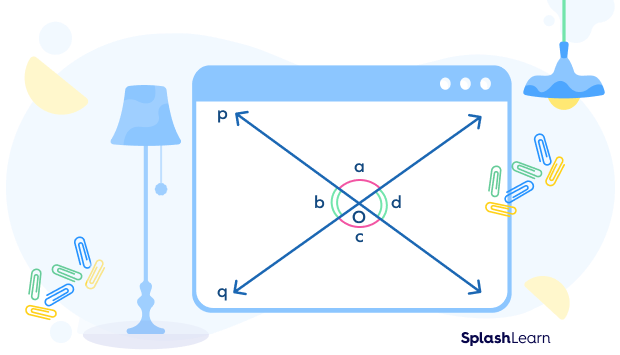
- Adjacent Angles (Bold)
Adjacent angles are the angles that share a common vertex and a common side.
In the figure given below, the pair of adjacent angles is:
(i) a and b
(ii) b and c
(iii) c and d
(iv) a and d
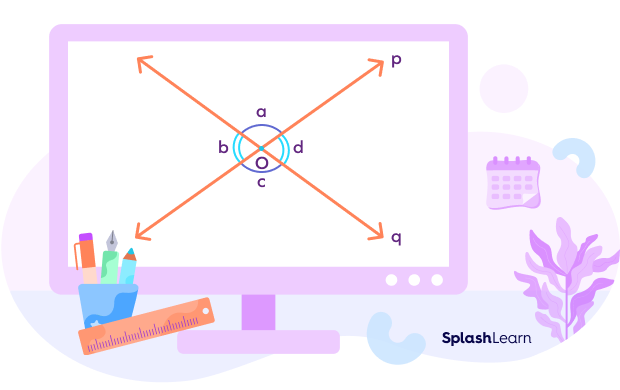
- Vertically Opposite Angles (Bold)
If two lines intersect each other, they form a pair of non-adjacent angles known as vertically opposite angles. The vertically opposite angles are equal to each other. In the figure given below, lines p and q intersect each other. Pairs of vertically opposite angles are a and c; b and d.
- Pair of Straight Angles or Linear Pair of Angles (Bold)
If the sum of measures of two adjacent angles is 180 degrees, then they are called angles in linear pair. A linear pair of angles forms a straight line when combined.
Here, angles a and b, angles a and d, angles b and c, and angles c and d form a linear pair.
In the figure given below:
a + b = 180°
b + c = 180°
c + d = 180°
a + d = 180°
What Are Parallel Lines?
Parallel lines are a pair of lines that never intersect and remain equidistant from each other at all points.
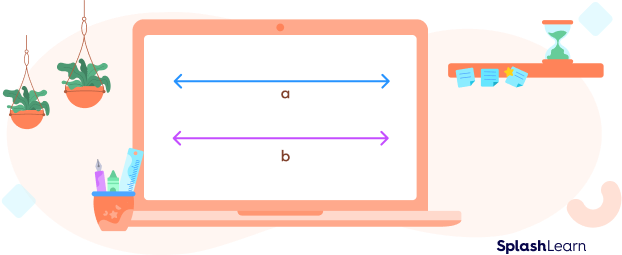
In the figure given above, lines a and b are parallel lines. They never meet and the perpendicular distance between them is always the same.
Facts about Intersecting Lines
- Intersecting lines meet at a common point called the point of intersection.
- At the point of intersection, intersecting lines create four angles: two pairs of opposite angles and two pairs of adjacent angles.
- Opposite angles formed by intersecting lines are congruent, meaning they have equal measures.
- Perpendicular lines are two lines that intersect each other at a right angle.
Conclusion
In this article, we learnt about intersecting lines, angles formed by them, parallel lines, and the point of intersection. Let’s solve a few examples and practice problems based on intersecting lines!
Solved Examples on Intersecting Lines
1. Answer the following questions based on the information given in the diagram.
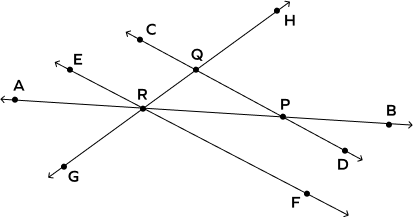
(a) Lines $\overleftrightarrow{GH}$ and $\overleftrightarrow{CD}$ are _____ lines.
(b) Lines $\overleftrightarrow{EF}$ and $\overleftrightarrow{CD}$ are _____ lines.
(c) Which line segments are intersecting? Give one example.
Solution: (a) $\overleftrightarrow{GH}$ and $\overleftrightarrow{CD}$ intersect each other at one point, which is Q. So, they are intersecting lines.
(b) Lines $\overleftrightarrow{EF}$ and $\overleftrightarrow{CD}$ do not intersect each other. The distance between $\overleftrightarrow{EF}$ and $\overleftrightarrow{CD}$ remains constant. So, they are parallel lines.
© Line segments PQ and PR intersect at the point P.
2. Two lines intersect each other at Point E as given in the figure. Find m∠QEY.
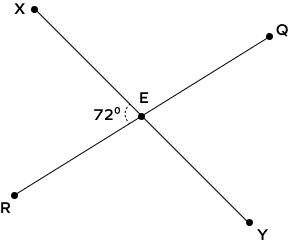
Solution: When two lines intersect each other, vertically opposite angles are equal.
So, m∠XER = m∠QEY
m∠QEY = 72°
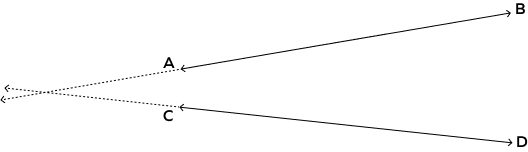
3. Are the lines $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ intersecting? Explain why or why not.
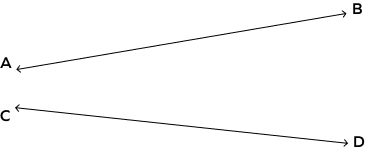
Solution: Yes. Lines $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ , if extended further, will intersect each other.
Practice Problems on Intersecting Lines
Intersecting Lines - Definition, Properties, Facts, Examples, FAQs
Identify the pair of parallel lines in the figure given below.
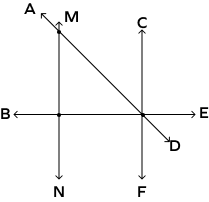
$\overleftrightarrow{MN}$ and $\overleftrightarrow{CF}$ do not intersect each other. So, they are parallel.
What are the types of angles formed by the two intersecting lines?
Two lines that intersect each other form vertically opposite angles, angles in linear pairs, and adjacent angles.
Which of the following statements is true?
Two lines intersect each other at one point only.
Find the measure of ∠AXZ.

Here, m∠AXY = 30°
m∠AXZ + m∠AXY = 180° (Linear Pair)
m∠AXZ = 180° – 30° = 150°
Frequently Asked Questions on Intersecting Lines
What are skew lines?
Skew lines are lines that are not on the same plane and do not intersect and are not parallel. For example, a line on the wall of your room and a line on the ceiling. These lines do not lie on the same plane. If these lines are not parallel to each other and do not intersect, then they can be considered skew lines.
What does it mean when two lines intersect each other in a coordinate plane?
When two lines intersect each other in a coordinate plane, it means that they have a common solution. For example: x + 3y = 9 and x + 2y = 6 have a common solution at (0, 3).
What is the range of the angle formed by two intersecting lines?
The angle formed between two intersecting lines is greater than 0° and less than 180°.
What are coplanar lines?
Two or more lines that lie in the same plane are said to be coplanar. Any two lines that intersect each other must lie in the same plane, and therefore are coplanar.
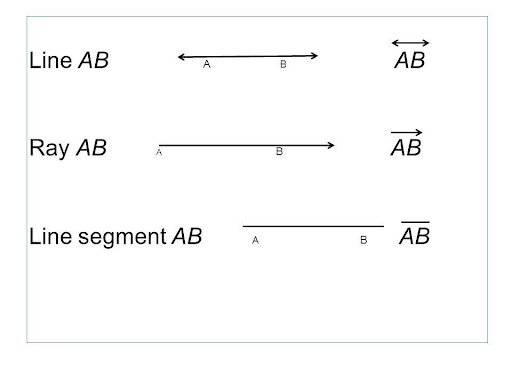
What’s the difference between a line, a line segment and a ray?
Line: A line extends indefinitely in both directions with no endpoints. Its length cannot be measured.
Ray: A ray is a part of a line. It has one fixed starting point but no endpoint. It extends indefinitely in one direction.
Line Segment: A line segment has two endpoints. It has definite length.