Area of a Shape

Area of a Shape

A shape is defined as a figure enclosed by a boundary. We see uncountable objects around us in shapes such as square, rectangle, circle etc. 

Now, what is this area of shape? Let’s dive deeper into the concept.

The area of shape is the space enclosed within the perimeter or the boundary of a given shape. We can calculate the area of shape for different geometrical shapes using specific mathematical formulae.

Area of Basic Geometric Shapes

How do you find the area of a shape? Let’s explore the area of various shapes and their area formulae. One great way to understand the area of shapes formulas is to make a formula chart! However, we will try to understand them one by one.

Rectangle

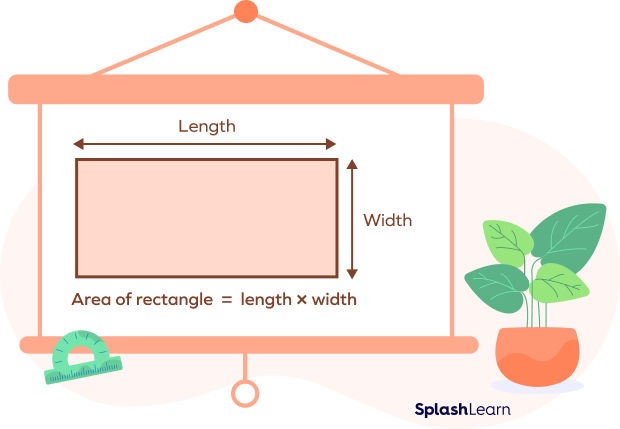
The area of a rectangle can be defined as the amount of space covered by a flat surface of a rectangle. It is calculated as the product of its length (l) and width (w). 

Area of a Rectangle $= \text{l} \times \text{w}$

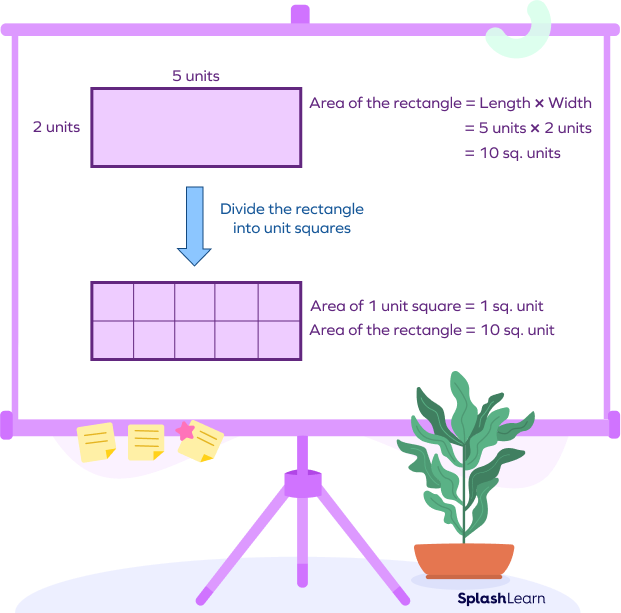
Let’s understand why by dividing the rectangle with length 5 units and width 2 units into unit squares. Unit squares are squares with side 1 unit and area equal to 1 square unit. 

Square

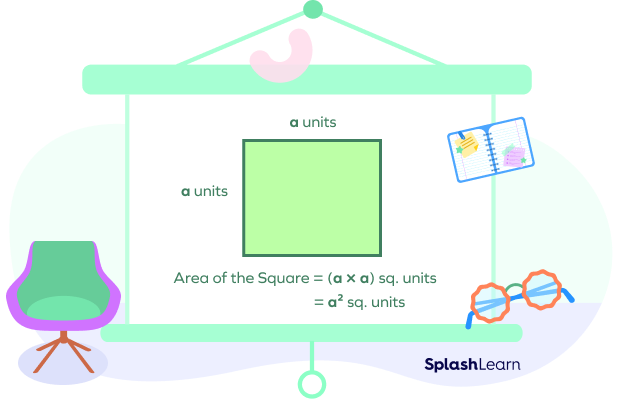
Squares are also rectangles with length equal to width. So, the area of a square can be calculated by multiplying its side (a) two times or finding its square. 

Area of Square $= \text{side} \times \text{side} = \text{side}^2$

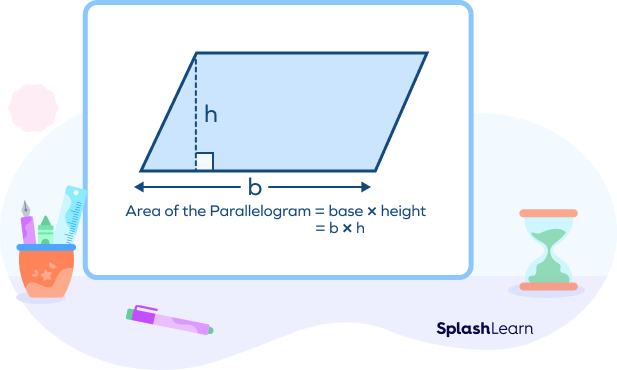
Parallelogram

The area of a parallelogram can be calculated by multiplying its base with the height. The base and the height of a parallelogram are perpendicular to each other. The formula to calculate the area of a parallelogram can be given as,

Area of parallelogram $= b \times h$ sq. units

Where, b is the length of the base and h is the height.

Do you wonder how this is so? 

Let’s do an activity to find out. 

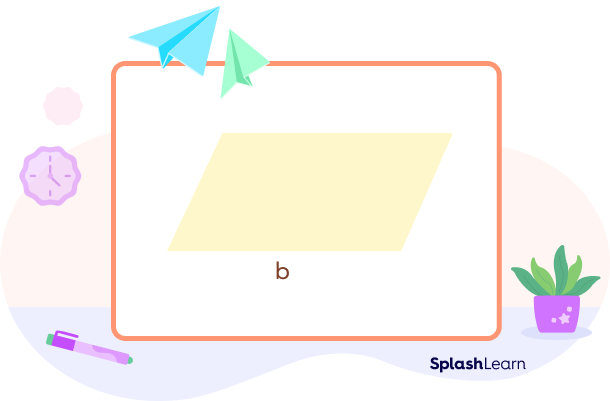
Step 1: Cut out a parallelogram with a base of any length, say, b units. 

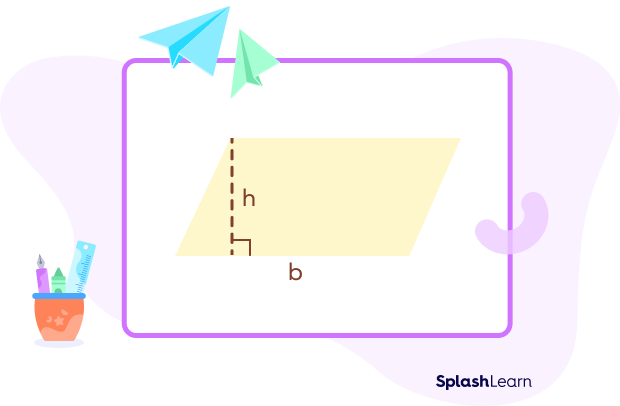
Step 2: Draw an altitude of length h units perpendicular to the base.

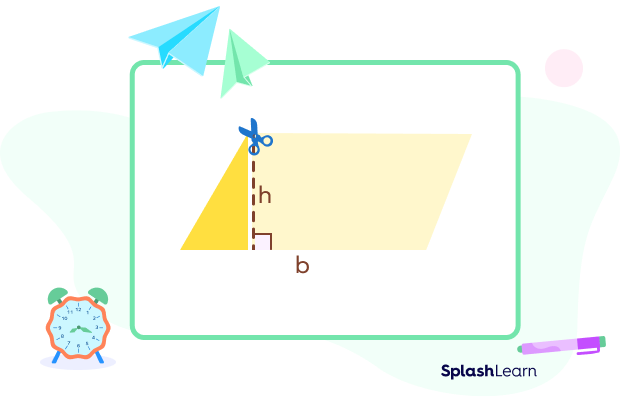
Step 3: Cut the right triangle so formed. 

Step 4: Place the cut right triangle on the opposite side to get a rectangle of length b units and width h units.

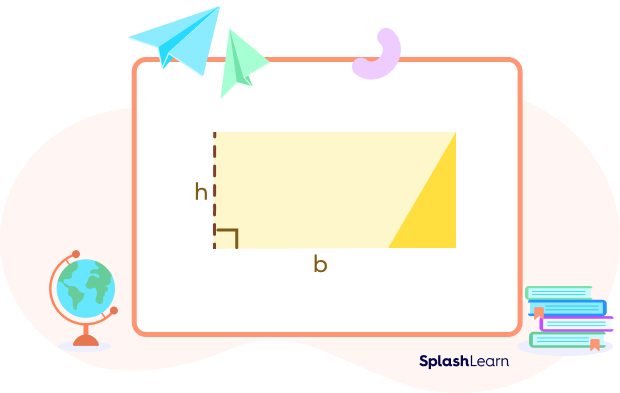
We know that the area of a rectangle is the product of its length and its width. So, the area of the rectangle so formed in the above activity would be $b \times h$ sq. units. 

Also, the area of the above rectangle will be equal to the area of the parallelogram we originally started with. 

Since we had cut a part of the parallelogram and placed it on the other side, the area of the figure will not change. This means, the area of the parallelogram would be equal to the area of the rectangle so formed. That is, $b \times h$ sq. units.

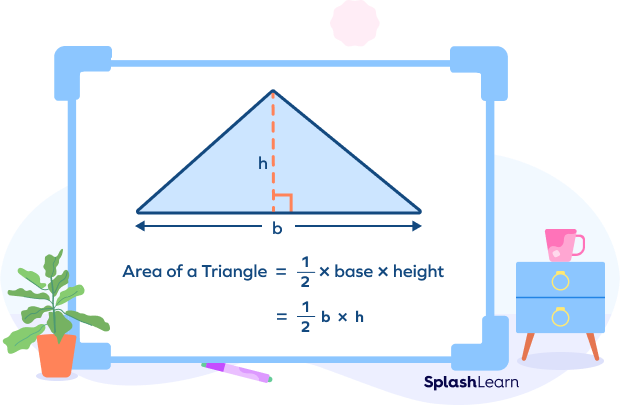
Triangle

We can find the area of a triangle using the formula: $\frac{1}{2}  \times \text{base} \times \text{height}$

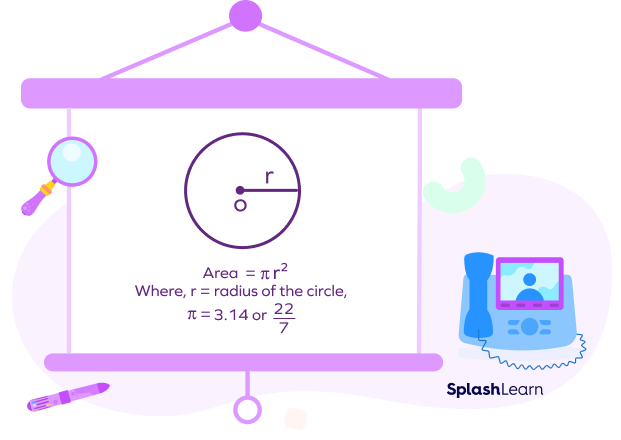
Circle

The area of a circle is calculated using the formula: $\pi r^2$, 

where r is the radius of the circle and pi $(\pi)$ is a constant that equals 22/7 or 3.14 (approximately). 

Do you know that if we divide a circle’s circumference by its diameter, the quotient is a constant that equals the value of pi $(\pi)$?

This means, $\pi =$ circumference/diameter

How Do We Apply Formula to Find the Area of a Shape?

• Identify parameters like length, width, side, radius, etc., that are required to find the area of a shape.

• Measure the parameters and make sure that all of them have the same units. For example, if the length of a rectangle is measured in inches, then the width should also be in inches only.

• Substitute these values in the formula.

• Calculate the area of shape.

Now let’s try finding the area of this triangle with base $= 20$ mm and height $= 5$ cm. 

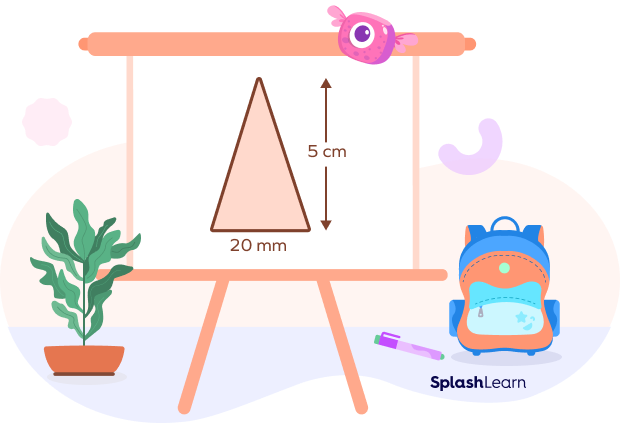
The formula to find the area of a triangle is $\frac{1}{2} \times \text{base} \times \text{height}$. 

So, to find the area of a triangle, we must know its base length and corresponding height, which we are already provided. 

However, these measurements are given in different units (base $= 20$ mm and height $= 5$ cm).

So, let’s convert 20 mm into cm, that is, 2 cm.

Now, we substitute the values in the formula and calculate the area. 

Area $= \frac{1}{2}  \times \text{base} \times \text{height} = \frac{1}{2} \times 2 \times 5 \text{cm}^2 = 10 \text{cm}^2$

Area of Combination of Shapes

How do we calculate the area of shapes that look like a combination of many different shapes? The area of a figure composed of other shapes can be calculated by adding the individual areas!

The answer to this question is very simple. We identify the shapes the figure is composed of, and find the area of the individual shapes. The sum of the individual areas gives us the required answer! 

Take a look at the following shape. What is the area of the figure?

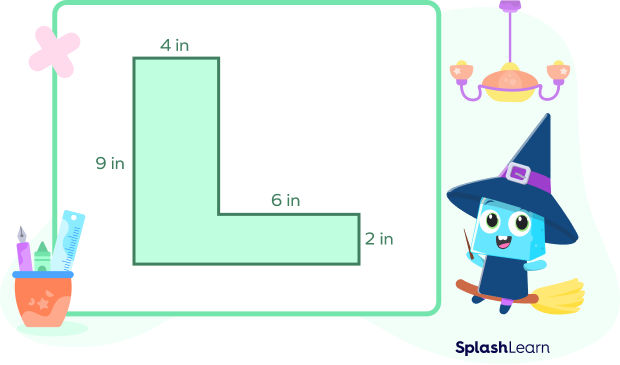
If we observe this shape carefully, we find that it is composed of two rectangles as shown below. 

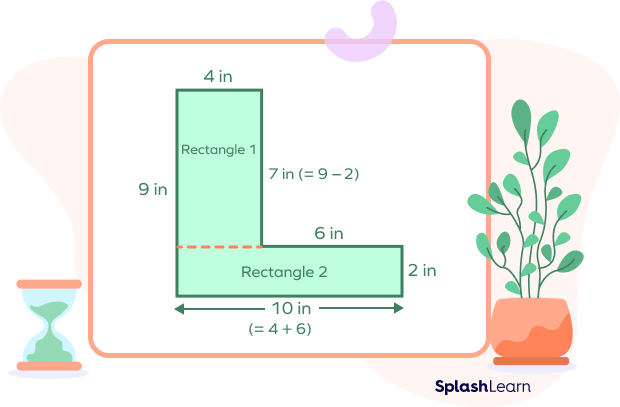
Now let’s find the area of each rectangle

Rectangle 1:

Length $= 4 \text{in}$, width $= 7 \text{in} (= 9 – 2 \text{in})$

Area $= (4 × 7) \text{in}^2 = 28 \text{in}^2$

Rectangle 2:

Length $= 10 \text{in} (= 6 + 4 \text{in}), width = 2 \text{in}$

Area $= (10 × 2) \text{in}^2 = 20 \text{in}^2$

Area of given figure $=$ area of Rectangle $1 +$ area of Rectangle 2

$= (28 + 20) \text{in}^2 = 48 \text{in}^2$

Solved Examples

1. The length of the largest chord of a circle is 14 ft. Find the area of the circle. (Use $=227$) 

Solution:

The longest chord of a circle is its diameter. This means, according to the question, diameter (d) $= 14$ ft.

We know that radius is half the diameter.

r $= \frac{d}{2} = 142 ft = 7$ ft

Using the formula for the circle’s area,

Area of a Circle $= r^2 = (227) \times (7)^2 = (227) \times 7 \times 7 = 22 \times 7 = 154 ft^2$

2. Find the area of a triangle with a base of 12 inches and a height of 5 inches.
Solution:
Let’s find the area using the area of triangle:
Area of triangle $= \frac{1}{2} \times \text{b} \times \text{h}$
A $= \frac{1}{2}  \times 12 \times 5$
A $= \frac{1}{2} \times 60$
Hence, the area of the triangle $= 30 \text{in}^2$

3. What is the area of a square-shaped mat with one side equal to 5 m?
Solution:
We know that one side of the mat is 5 m. So, we will use the formula: Area of a square $= \text{side} \times \text{side} = 5 \times 5 = 25 \text{m}^2$. Hence, the area of the swimming pool is 25 square meters.

4. The length and width of a rectangular farm are 80 yards and 60 yards. Find the area of shape.
Solution:
Length of the farm, l = 80 yards and width of the farm, $\text{w} = 60$ yards
Area of the rectangular farm is given by $= \text{l} \times \text{w} = 80 \text{yd} \times 60 \text{yd} = 4800 \text{yd}^2$.
Therefore, the area of the farm is 4800 sq. yd.5. Calculate the area of a solar cell sheet that is in the shape of a parallelogram, given that the base measures 20 in, and the altitude measures 8 in.
Solution:
Using the area of parallelogram formula:
Area of the solar cell sheet $= \text{b} \times \text{h} = (20) \times (8) = 160 \text{in}^2$
So, the area of a solar cell sheet is $160 \text{in}^2$.

Practice Problems

Frequently Asked Questions