What Is the Midpoint Formula? Examples, Derivation, Facts, FAQs

What Is the Midpoint of a Line Segment?

The midpoint of a line segment is the point that lies exactly at the center of a line segment, dividing it into two equal parts. The bisector of a line segment passes through the midpoint.

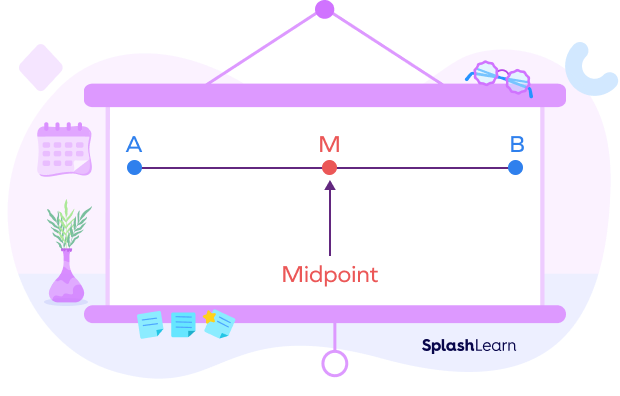
In the diagram shown below, the point M is the midpoint of line segment AB.

The points A and B are endpoints of AB.

What Is the Midpoint Formula?

The midpoint formula is used to find the coordinates of the midpoint of a line segment using the coordinates of the endpoints.

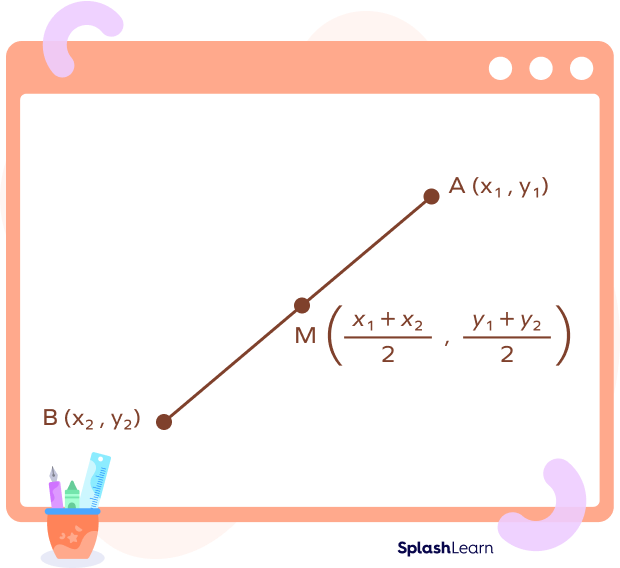
Suppose a line segment has two endpoints, P(x₁, y₁) and Q(x₂, y₂). The midpoint formula defines the coordinates of the midpoint M(x₃, y₃) as

$x_{3} = \frac{x_{1} + x_{2}}{2}$

$y_{3} = \frac{y_{1} + y_{2}}{2}$

Thus, the coordinates of the midpoint M are $(\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2})$.

How to Find the Midpoint

Let’s discuss methods that are commonly used to determine the midpoint of a line segment.

1. Formula Method

Use the midpoint formula to find the coordinates of the midpoint. 

Example: The points P(-4, 2) and Q(2, 2) are the endpoints of the line segment PQ.

So, to find the midpoint of the line segment, we use the formula: 

$(x, y) =  (\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2})$

$(x, y) = (\frac{-4 + 2}{2},\; \frac{2 + 2}{2})$

$(x, y) = (-1, 2)$

Thus, M(-1, 2) is the midpoint of the line segment PQ.

2. Graph Method

Using the graph, find the length of the line segment. Divide the length of the segment by 2.  Measure this distance from any one of the endpoints to find the midpoint. 

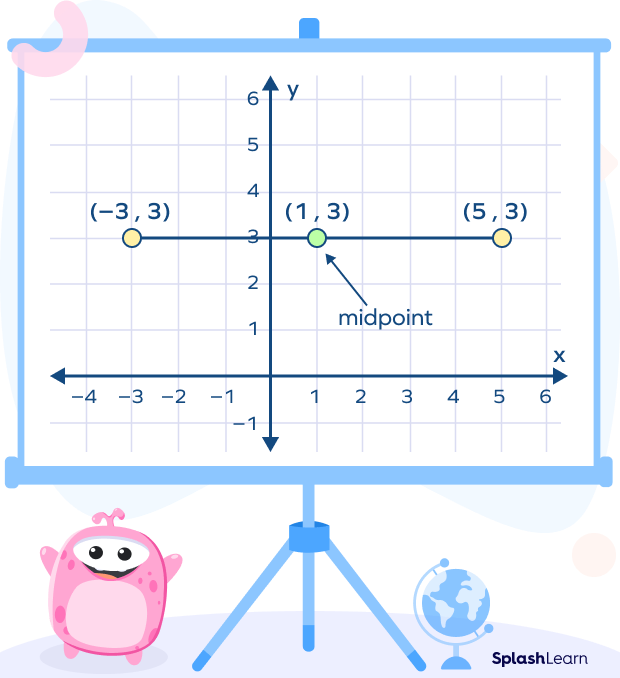
Example: Consider the line segment with endpoints (-3, 3) and (5, 3).

Length of the line segment = 8 units

$8 \div 2 = 4$

If you count 4 units to the right from (-3, 3), you land on (1, 3).

(-3 + 4, 3) = (1, 3)

If you count 4 units to the left from (5, 3), you land on (1, 3).

(5 – 4, 3) = (1, 3)

Therefore, the point (1, 3) is the midpoint.

Other Important Formulas related to the Midpoint

There are a number of formulas related to the midpoint formula. Some of them are mentioned below:

1. Distance formula: 

To calculate the distance between two points with coordinates (x₁, y₁) and (x₂, y₂), use the following formula: 

$d = \sqrt{(x_{2} \;-\; x_{1})^{2} + (y_{2} \;-\; y_{1})2}$

2. Slope formula: 

To calculate the slope of a straight line passing through two points (x₁, y₁) and (x₂, y₂), use the following formula:

$m = \frac{y_{2}\; -\; y_{1}}{x_{2} \;-\; x_{1}}$

3. Centroid of Triangle Formula:

The point of intersection of the medians of a triangle is the centroid of a triangle. The vertices of a triangle (x, y) are given as:

$x = \frac{(x_{1} + x_{2} + x_{3})}{3}$

$y = \frac{(y_{1} + y_{2} + y_{3})}{3}$

4. Equation of a Line:

To find the equation of a line passing through two points (x₁, y₁) and (x₂, y₂), you can use the slope formula and point-slope form of the equation: 

$y\;-\;y_{1} = m(x\;-\;x_{1})$

5. Section Formula:

• Internal section formula: It is used to find the coordinates of a point R (x, y) dividing a line segment joining points A(x₁, y₁) and B(x₂, y₂) internally in the ratio m : n.

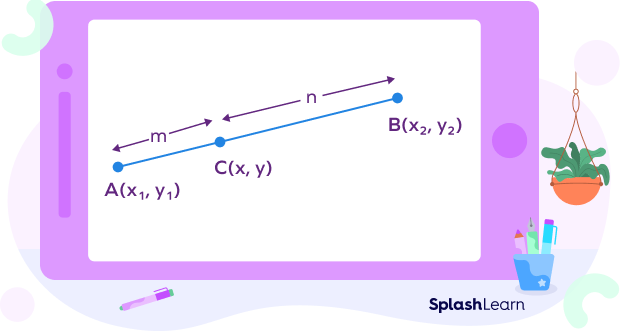
$x = \frac{(mx_{2} + nx_{1})}{(m + n)}$

$y = \frac{(my_{2} + ny_{1})}{(m + n)}$

• External section formula: It is used to find the coordinates of a point R (x, y) dividing a line segment joining points A(x₁, y₁) and B(x₂, y₂) externally in the ratio m : n.

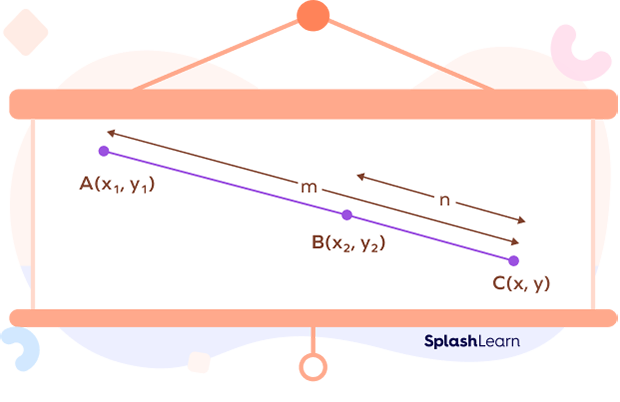
$x = \frac{mx{2} \;-\; nx_{1}}{m \;-\; n}$

$y = \frac{my_{2} \;-\; ny_{1}}{m \;-\; n}$

Midpoint Formula Derivation

Consider the line segment AB with endpoints A(x_A, y_A) and B(x_B, y_B).

Let’s write the coordinates of the midpoint M as M(x_M, y_M).

Consider the points on the X-axis and Y-axis given by

X_A= (x_A,0), Y_A= (0,y_A)

X_B= (x_B,0), Y_B= (0,y_B)

X_M= (x_M,0), Y_B= (0,y_M)

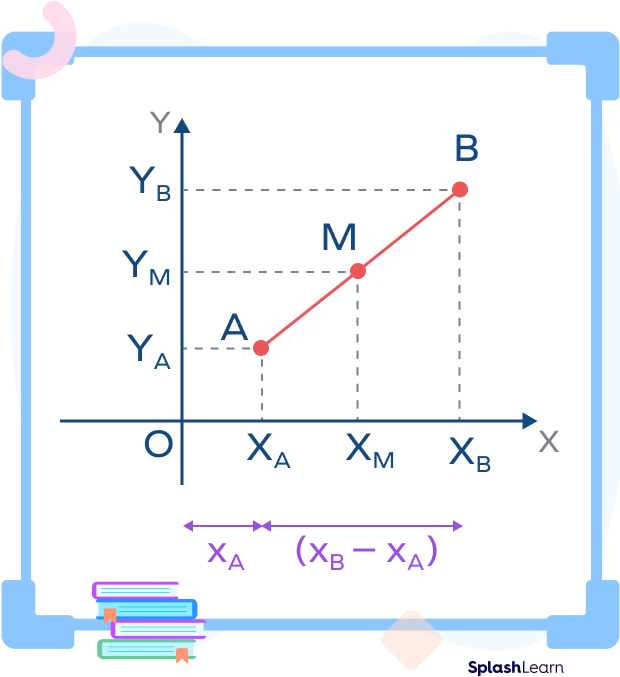
Distance OX_M = X-coordinate of midpoint M = x_M

x_M = OX_A + X_AX_M

x_M $= x_{A} + \frac{x_{B}\;-\;x_{A}}{2}$

x_M $= \frac{2x_{A}}{2} + \frac{x_{B}\;-\;x_{A}}{2}$

x_M $= \frac{x_{B} + x_{B}}{2}$

Similarly, 

Distance OY_M = Y-coordinate of midpoint M = y_M

y_M = OY_A + Y_AY_M

y_M $= y_{A} + \frac{y_{B}\;-\;y_{A}}{2}$

y_M $= \frac{2yA}{2} + \frac{yB-yA}{2}$

y_M $= \frac{y_{A} + y_{B}}{2}$

Facts about Midpoint Formula

Conclusion

In this article, we learned about the midpoint, midpoint formula and its significance in geometry for finding the coordinates of the midpoint. Understanding the midpoint formula has various mathematical applications. For hands-on practice and better understanding, let’s now explore a few examples and MCQs. 

Solved Examples on the Midpoint Formula

Example 1: The midpoint of a line segment AB is (2, –1). Find the coordinates of point B if that of point A are (–3, 5).

Solution:

Let’s write the coordinates of point B as (x₂, y₂).

Putting it in the midpoint formula, we get

$(x, y) = (\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2})$

$\frac{(\;-\;3 + x_{2} )}{2}  = 2$

Thus, $x_{2} = 7$

$\frac{(5 + y_{2})}{2}  = \;-\;1$

Thus, $y_{2} = \;-\;7$

So, the coordinates of point B are (7, -7).

2. What are the coordinates of the midpoint of a line segment whose endpoints are (4, 1) and (–2, 3)?

Solution:

Let’s write the coordinates of the midpoint as (x, y).

We will use the endpoints of the line segment to find the midpoint.

$(x, y) = (\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2})$

$(x, y) = (\frac{4 + (-2)}{2},\; \frac{1 + 3}{2})$

(x, y) = (1, 2)

So, the coordinates of the midpoint are (1, 2).

3. If the midpoint of the line segment AB is (3, 4) and point A is (5, 6), what will be the coordinates of point B?

Solution:

Let’s write the coordinates of point B as (x, y).

Let us apply the given values in the midpoint formula:

$(x, y) = (\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2})$

$x = \frac{x_{1} + x_{2}}{2}$

$y = \frac{y_{1} + y_{2}}{2}$

Given: A = (5, 6) and midpoint = (3, 4)

$3 = \frac{5 + x_{2}}{2}$

$x_{2} = 1$

$4 = \frac{6 + y_{2}}{2}$ 

$y_{2} = 2$

So, the coordinates of point B are (1, 2).

4. Find the midpoint of the line segment that connects the endpoints (–3, 5) and (7, –2).

Solution:

Let’s write the coordinates of the midpoint M as M(x, y).

We can calculate the value of M(x, y) by applying the midpoint formula:

$x = \frac{\;-\;3 + 7}{2} = 2$

$y = \frac{5 \;-\; 2}{2} = 1.5$

So, the M(x, y) midpoint coordinates of the line segment are (2, 1.5).

5. If the midpoint of a line segment with endpoints (1, h) and (7, 5) is (4, –1), find the value of h.

Solution:

To find the value of h, we will use the formula for the y-coordinate of the midpoint.

$y = \frac{y_{1} + y_{2}}{2}$

Given: Midpoint = (4, -1)

Endpoints are (1, h) and (7, 5).

$y = \frac{y_{1} + y_{2}}{2}$

$\;-\;1 = \frac{h + 5}{2}$

$h = \;-\;7$

Therefore, the y-coordinate of the endpoint (1, h) is -7.

Practice Problems on the Midpoint Formula

Frequently Asked Questions about Midpoint Formula