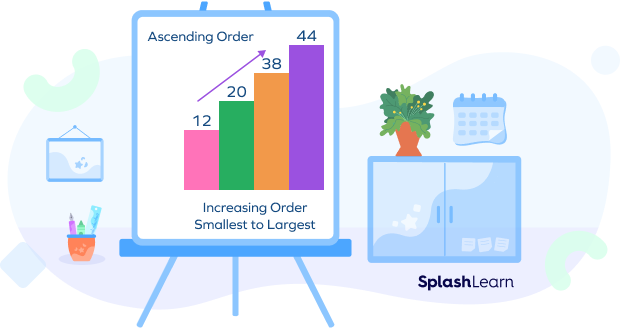
What Is Ascending Order?
Ascending order is an arrangement of numbers in increasing order. It is the method of arranging the numbers from smallest to largest. It is also known as increasing order.
Example 1: The set of whole numbers in ascending order:
0 < 1 < 2 < 3 < 4 < 5 < 6 … and so on.
Example 2: Kids standing in the ascending order of their heights (from shortest to tallest).

Recommended Games
Ascending Order: Definition
Ascending order can be defined as the arrangement of numbers from the smallest to the greatest.
Recommended Worksheets
Symbol Used to Write Ascending Order
We can represent a given set of numbers in ascending order by using the “less than” symbol (<).
a < b means a is less than b.
For example, the numbers 5, 8, 3, 9, 1 arranged in the ascending order are
1 < 3 < 5 < 8 < 9
Ascending Order on a Number Line
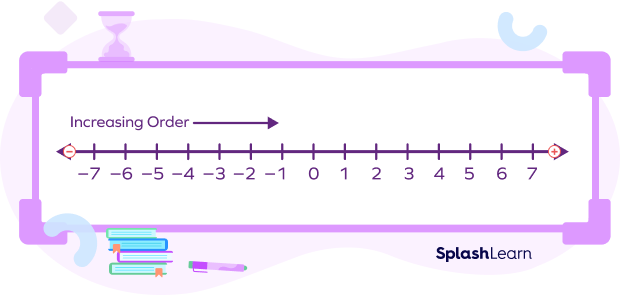
A number line is the easiest way to understand ascending order. You can observe that the numbers from -7 to 7 are arranged in ascending order. On a number line, as you go from left to right, the numbers increase.
Arranging Integers In Ascending Order
The set of integers include the set of positive integers {1, 2, 3, 4…}, the set of negative integers {-1, -2, -3, …}, and 0.
Let’s understand how to arrange positive integers and negative integers in ascending order.
Positive Integers in Ascending Order
To arrange positive integers in ascending order, we first compare the numbers using place values.
- The number that has the least number of digits is the smallest number.
- The number that has the most number of digits is the largest number.
- In case the number of digits is the same, then we compare the digits at the highest place value (leftmost digits).
- Compare all the numbers in the same manner and finally arrange them all from smallest to largest.
Example: 130, 62, 10766, 625, 8000
62 has two digits, the least number of digits. Thus, it is the smallest number.
10766 has five digits. It is the largest number.
130 and 625 has same digits, Comparing their leftmost digit, we get 1 < 6
Thus, 130 < 625
8000 has more digits than 625. So, 625 < 8000
Arranging in ascending order, we get
62 < 130 < 625 < 8000 < 10766
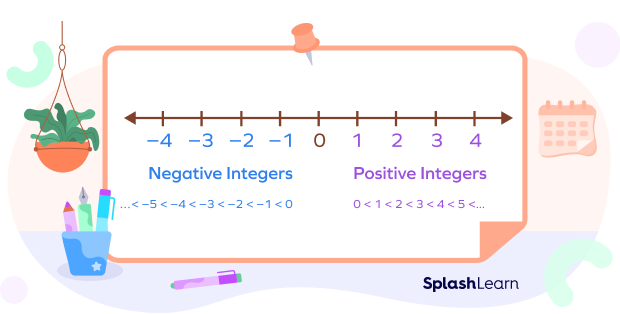
Negative Integers in Ascending Order
To arrange negative integers in ascending order, understand that the numbers decrease as we go from left to right on a number line.
We can simplify this with the following rules:
If a > b, then ( – a) < ( – b).
If a < b, then ( – a) > ( – b).
Example 1: We know that 8 > 5.
Thus, – 5 < – 8
Example 2: 10 is greater than 8, but -10 is smaller than -8.
Decimals in Ascending Order
To arrange decimals in ascending order, we first compare them using the place values. To compare decimals, we can use the place value chart. We start by comparing the digits at the highest place value (leftmost digit). If they match, we move to compare the next digit.
Suppose we have to arrange 0.09, 1.12, 0.32, 1.11 in ascending order.
| Ones | Decimal Point | Tenth | Hundredth |
|---|---|---|---|
| 0 | . | 0 | 9 |
| 0 | . | 3 | 2 |
| 1 | . | 1 | 2 |
| 1 | . | 1 | 1 |
Comparing the digits starting from the highest place value, we get
0.09 < 0.32 < 1.11 < 1.12
Fractions in Ascending Order
Let’s discuss different possible cases when arranging fractions in ascending order and methods we can consider.
Converting Fractions to Decimals
Convert the given set of the fractions into decimal numbers and then arrange the decimals in ascending order.
Example: Arrange $\frac{2}{3},\;\frac{1}{2},\;\frac{5}{6},\;\frac{4}{5}$ in ascending order.
$\frac{2}{3} = 0.66,\;\frac{1}{2} = 0.5,\; \frac{5}{6} = 0.83,\; \frac{4}{5} = 0.80$
0.5 < 0.66 < 0.80 < 0. 83
$\frac{1}{2} < \frac{2}{3} < \frac{4}{5} < \frac{5}{6}$
Fractions with Same Numerators
When the fractions have the same numerator, the fraction with the highest denominator is the smallest.
Example: Arrange $\frac{1}{8},\;\frac{1}{2},\;\frac{1}{7},\;\frac{1}{5}$ in ascending order.
Numerator = 1
Compare the denominators.
2 < 5 < 7 < 8
Thus, $\frac{1}{8} < \frac{1}{7} < \frac{1}{5} < \frac{1}{2}$
Like Fractions in Ascending Order
Like fractions are the fractions that have the same denominator. To compare like fractions, we simply compare the numerators.
Example: Arrange $\frac{6}{7},\;\frac{2}{7},\;\frac{1}{7},\;\frac{4}{7}$ in ascending order.
Arranging the numerators in the ascending order, we get
1 < 2 < 4 < 6
$\frac{1}{7} < \frac{2}{7} < \frac{4}{7} < \frac{6}{7}$
Unlike Fractions in Ascending Order
To compare unlike fractions, we first make the denominators of the fractions the same by finding the LCM of the denominators and then compare and arrange them in ascending order.
For example: Arrange $\frac{2}{3},\;\frac{1}{2},\;\frac{5}{6},\;\frac{4}{5}$ in ascending order.
LCM (2, 3, 5 and 6) = 30
$\frac{2}{3} = \frac{20}{30},\; \frac{1}{2} = \frac{15}{30},\; \frac{5}{6} = \frac{25}{30},\; \frac{4}{5} = \frac{24}{30}$
$\frac{15}{30} < \frac{20}{30} < \frac{24}{30} < \frac{25}{30}$
$\Rightarrow \frac{1}{2} < \frac{2}{3} < \frac{4}{5} < \frac{5}{6}$
Ascending Order of Alphabets (A-Z)
Ascending order means going up from smallest value to highest value. Thus, alphabets in ascending order are written from A to Z.
Facts on Ascending Order
- Ascending order arranges values from the smallest to the largest.
- It is commonly used in sorting numbers, letters, or other data.
- In ascending order, the first element is the smallest, and subsequent elements increase gradually.
- Ascending order is opposite to descending order, which arranges values from largest to smallest.
Conclusion
In this article, we learned about the ascending order of numbers and the significance of ascending order in arranging and comparing values. Understanding this concept is essential for various applications, from sorting data to making informed decisions. To solidify our knowledge, let’s explore some examples and engage in MCQs for better comprehension.
Solved Examples on Ascending Order
1. Arrange these heights in ascending order:
2 feet 7 inches
3 feet 5 inches
2 feet 2 inches
3 feet 2 inches
3 feet 8 inches
3 feet 6 inches
Solution:
To arrange the heights in ascending order, we write the heights from the lowest to the highest.
2 feet 2 inches < 2 feet 7 inches < 3 feet 2 inches < 3 feet 5 inches < 3 feet 6 inches < 3 feet 8 inches
2. Arrange the integers –3, 0, –10, 4, –15, 18 in ascending order.
Solution:
Consider the positive integers 4, 18.
On comparing, we get 4 < 18
Positive integers are greater than 0.
Thus, 0 < 4 < 18
Consider the negative integers -3, -10, -15
We know that the numbers decrease as we go from left to right on a number line.
Also, 3 < 10 < 15
Thus, -15 < -10 < -3
The given integers in ascending order are
-15 < -10 < -3 < 0 < 4 < 18
3. Arrange the numbers in ascending order: 61570, 65701, 70561, 50176, 17065.
Solution:
The five numbers are 61570, 65701, 70561, 50176, 17065.
The number of digits are the same in all the numbers.
Start comparing the digits at the highest place value (leftmost digits). If it matches, move to the next place.
17065 < 50176 < 61570 < 65701 < 70651
Practice Problems on Ascending Order
Ascending Order – Definition, FAQs, Practice Problems, Examples
Ascending order is the arrangement of numbers
Ascending order is the arrangement of numbers from the smallest to the largest.
On arranging the words in ascending order according to the dictionary, which word will come in the end?
In the dictionary, the arrangement in ascending order will be: able, ant, apple, aunt. So, the word ‘aunt’ will come in the end.
On arranging $\frac{9}{11},\;\frac{2}{3},\;\frac{1}{6}$ in ascending order, we get
$\frac{2}{3} = 0.66,\; \frac{9}{11} = 0.81,\; \frac{1}{6} = 0.16$
$0.16 \lt 0.66 \lt 0.81$
$\frac{1}{6} \lt \frac{2}{3} \lt \frac{9}{11}$
Frequently Asked Questions on Ascending Order
What is the difference between ascending order and descending order?
Ascending order means increasing order. So, ascending order is the order in which a given set of numbers are arranged from smallest to highest. The symbol used for ascending order is “less than sign (<).”
On the other hand, descending order means decreasing order. So, descending order is to arrange the given set of numbers from highest to lowest. The symbol used for descending order is “more than sign (>).”
For example: 3 < 5 < 7 < 8 is ascending order whereas 8 > 7 > 5 > 3 is descending order.
What is the purpose of ascending order?
We use the ascending order in mathematics for data sorting, analysis, etc. It helps to make data easy to understand.
What is the ascending order for the dates?
When we talk about the dates, ascending order means that the oldest ones would come first and the most recent ones last.
For example: 21 September < 23 September < 30 September
Is descending order smallest to largest?
No. Descending order is from largest to smallest. The largest quantity or number is placed first and the smallest quantity or number is placed at the last position.
Can we arrange fractions in ascending or descending order?
Yes. Just like whole numbers, fractions can also be arranged in ascending or descending order.
What symbols are used when arranging numbers in ascending and descending order?
The symbols < (less than) and > (greater than) are used when arranging numbers in ascending and descending order.
Ascending order: 4 < 7 < 8 < 10
Descending order: 11 > 7 > 5 > 2
Do we look at the numerator or denominator when arranging fractions in ascending or descending order?
- If the numerators of a group of fractions are the same, the fraction with the highest denominator is the smallest.
- We compare numerators if the denominators are the same.
- If the denominators are different, we compare the decimal value or make the denominators the same using LCM method.




































