What Is the Perpendicular Bisector Theorem in Geometry?
According to the perpendicular bisector theorem, any point on the perpendicular bisector of a line segment is equidistant from both the endpoints of the line segment.
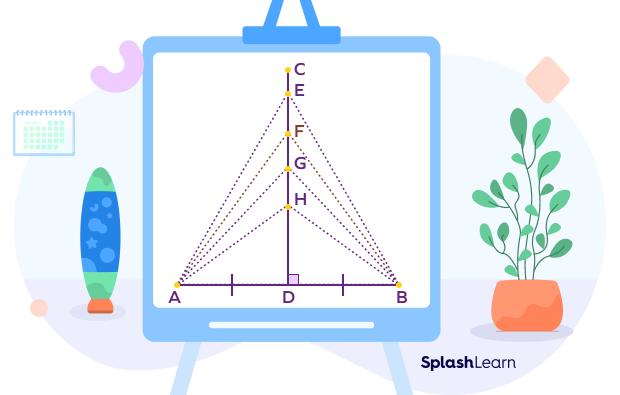
In the figure, CD is the perpendicular bisector of the line segment AB.
E, F, G, H, D are the distinct points on the perpendicular bisector.
By the theorem, we have
AH = BH
AG = BG
AF = BF
AE = BE
AD = BD
Recommended Games
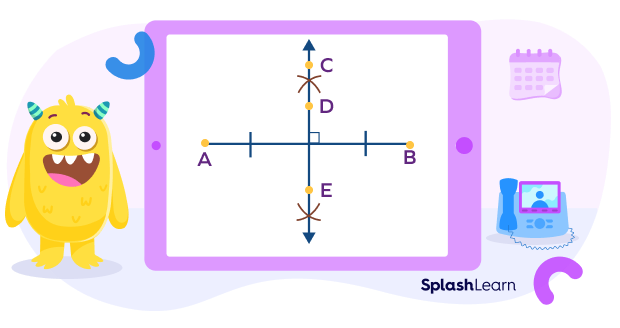
What Is a Perpendicular Bisector?
A line segment that intersects another line segment at a right angle and divides it into two equal parts at its midpoint is known as a perpendicular bisector.
In the given image, the line CE is the perpendicular bisector of the line segment AB.
What Is the Converse of the Perpendicular Bisector Theorem?
According to the converse of the perpendicular bisector theorem, if a point is equidistant from both the endpoints of the line segment in the same plane, then that point lies on the perpendicular bisector of the line segment.
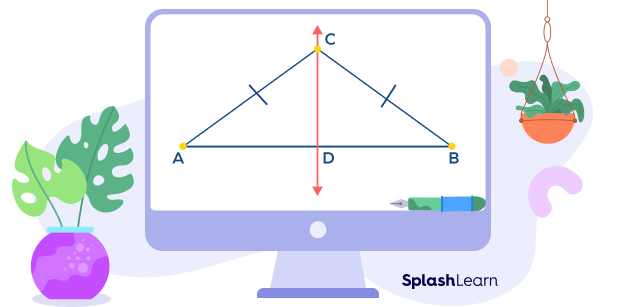
In the figure, AC = BC
The point C is equidistant from both the endpoints of the line segment AB.
It means that the point C lies on the perpendicular bisector of the line segment AB. Thus, the line CD is the perpendicular bisector of the line segment AB.
Proof of Perpendicular Bisector Theorem
Perpendicular Bisector Theorem Statement: Any point on the perpendicular bisector is equidistant from both the endpoints of the line segment on which it is constructed.
Take a look at the figure below, where P is any point on the perpendicular bisector of AB that intersects AB at Q.
Construction: Draw PA and PB using dotted lines.
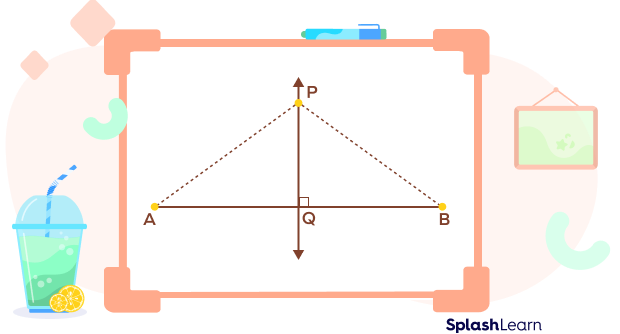
In ΔAPQ and ΔBPQ,
AQ = QB (since Q is the midpoint of AB)
m∠AQP = m∠BQP = 90°
PQ = PQ (common perpendicular)
∴ ΔAPQ ≅ ΔBPQ by the side-angle-side (SAS) congruence rule.
Hence, AP = BP, which implies that P is equidistant from A and B.
Proof of the Converse of Perpendicular Bisector Theorem
Statement: According to the converse of the perpendicular bisector theorem, if a point is equidistant from both the endpoints of the line segment in the same plane, then that point lies on the perpendicular bisector of the line segment.
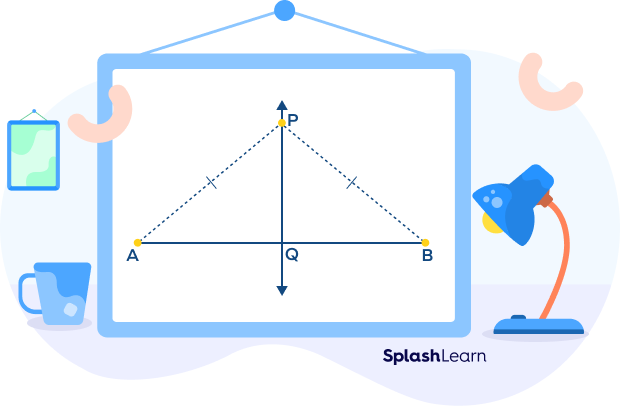
In the above figure, PA = PB
The point P is equidistant from A and B.
Construction: Draw a perpendicular line from point P that intersects line segment AB at point Q.
To prove: AQ = QB
In ΔAPQ and ΔBPQ,
PA = PB
PQ = PQ (common perpendicular)
∠AQP = ∠BQP = 90°
∴ ΔAPQ ≅ ΔBPQ by the SSA congruence criterion.
Hence, AQ = QB, which implies that Q is equidistant from A and B. Also, Q lies on a perpendicular bisector of AB.
Properties of a Perpendicular Bisector
- A perpendicular bisector divides any line segments AB into two equal halves or bisects it.
- It makes an angle of 900 with baseline segment AB.
- Every point of the perpendicular bisector is equidistant from the endpoints A and B of line segment AB.
How to Construct a Perpendicular Bisector
Using a compass and a ruler, follow these steps to create a perpendicular bisector of a line.
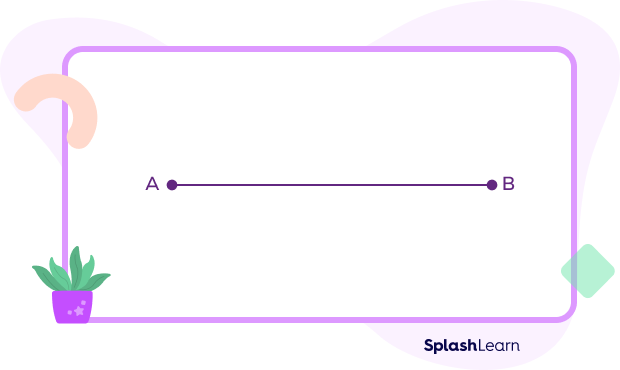
Step 1: Draw a line segment AB.
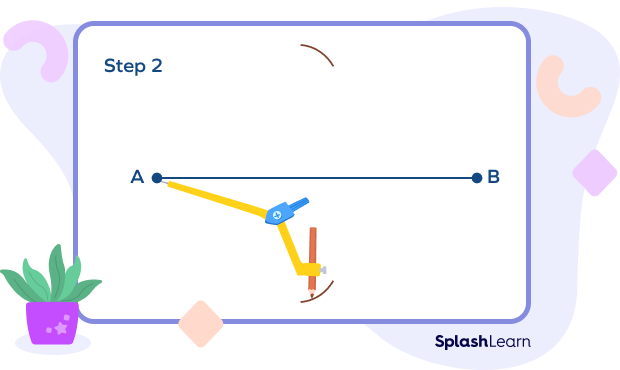
Step 2: Set the compass so that its length is slightly more than half of the length of AB. Now place the compass pointer at point A and draw arcs below and above the line.
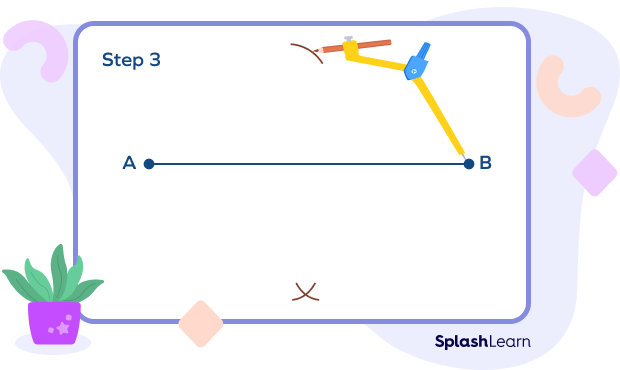
Step 3: Place the compass pointer at point B while maintaining the same length in the compass. Similarly, draw two arcs below and above the line.
Step 4: Mark the points where the opposite arcs cut at points P and Q. Using a ruler, draw a line PQ.
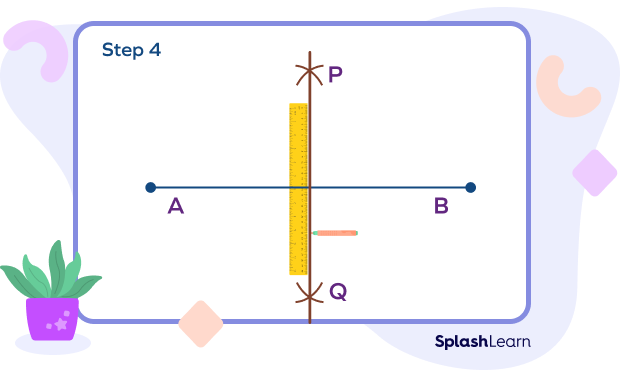
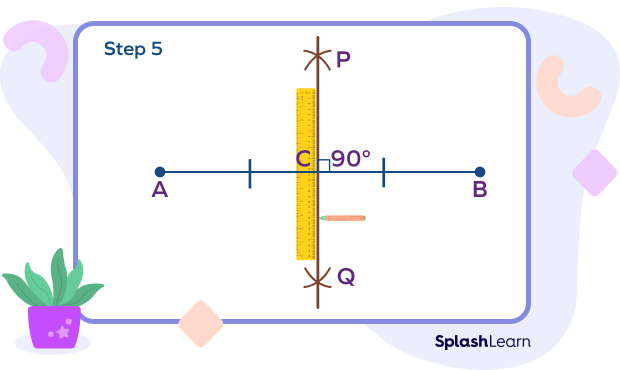
Step 5: PQ is the perpendicular bisector of the line segment AB. Mark the point of intersection of PQ and AB as C. Show AC = BC.
Facts about Perpendicular Bisector Theorem
- A perpendicular bisector of a side can be a median of a triangle.
- It is used extensively in making tables of different sizes and lengths, bridge construction, etc.
- For an equilateral triangle, the altitude, median, angle bisector, and perpendicular bisector for each side are all the same single line. These 3 (one for each side) lines also form the lines of symmetry of the triangle.
Conclusion
In this article, we learned about the perpendicular bisector theorem, converse of perpendicular bisector theorem, proofs, properties of a perpendicular bisector, and methods to draw a perpendicular bisector. Let’s solve a few examples and practice problems for a better understanding.
Solved Examples on Perpendicular Bisector Theorem
- If a perpendicular bisector is drawn to a 12 inches long line segment, what is the measure of each part of the line segment?
Solution:
We know, a perpendicular bisector intersects a line segment at the right angle and divides it into two equal parts.
The measure of the line segment is 12 inches.
The measure of each part thus formed $= \frac{12}{2} = 6$ inches.
- In the figure given below, a perpendicular bisector is drawn on side BC from the vertex A, making the angle of (5x+10)o with the base BC. Find the value of x by using the properties of the perpendicular bisector.
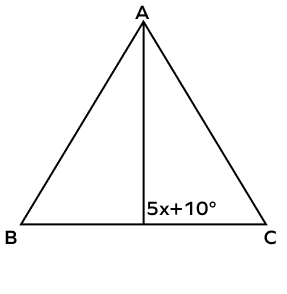
Solution:
Since the line is a perpendicular bisector of BC, it makes an angle of 90.
(5x + 10)o = 90o
5x + 10 = 90
5x = 90 – 10 = 80
5x = 80
$x = \frac{80}{5} = 16$
- Determine the value of x for the figure given below if AP is the perpendicular bisector of BC.
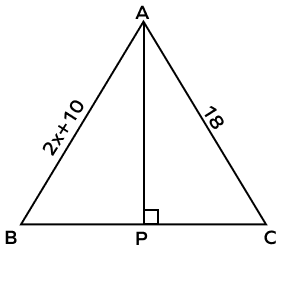
Solution:
According to the perpendicular bisector theorem, any point on the perpendicular bisector is equidistant from both the endpoints of the line segment on which it is drawn.
We have AB = AC
2x + 10 = 18
2x = 18 – 10
2x = 8
$x = \frac{8}{2} = 4$
- Find the value of x if AP is the perpendicular bisector of the side BC.
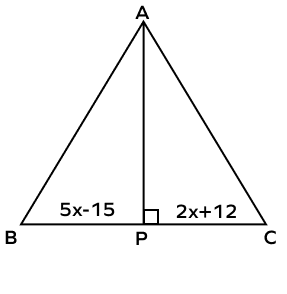
Solution:
According to the perpendicular bisector theorem, any point on the perpendicular bisector is equidistant from both the endpoints of the line segment on which it is drawn.
Thus, PB = PC
5x – 15 = 2x + 12
5x – 2x = 12 +15
3x = 27
$x = \frac{27}{3} = 9$
Practice Problems on Perpendicular Bisector Theorem
Perpendicular Bisector Theorem: Definition, Properties, Examples
Perpendicular bisector divides any line segment into ______ equal parts.
A perpendicular bisector bisects a line segment at a right angle. So, it divides the segment into two equal parts.
Perpendicular bisector meets line segment at _____ angle.
A perpendicular bisector intersects a line segment at a $90^{\circ}$ angle.
Line m is the perpendicular bisector of the line segment BC. Find the value of x.

By the perpendicular bisector theorem, we have
AC = BC
x + 6 = 14
x = 8
Frequently Asked Questions on Perpendicular Bisector Theorem
What is the statement of the perpendicular bisector theorem?
The perpendicular bisector theorem states that any point on the perpendicular bisector is equidistant from both the endpoints of the line segment on which it is drawn.
Can a triangle’s median be a perpendicular bisector?
Yes, a triangle’s median can be a perpendicular bisector. Every perpendicular bisector is a median, but not every median is a perpendicular bisector. A median is defined as a line segment from a vertex of a triangle to the midpoint of the side opposite to that vertex. So, if the median joins the opposite side at 90 degrees, it will be the perpendicular bisector of that side.
How many medians does a triangle have?
A triangle has three medians. A median is drawn from a vertex and passes through the midpoint of the opposite side.
What is the angle bisector theorem?
The angle bisector theorem states that in a triangle, the angle bisector of any angle will divide the opposite side in the ratio proportional to the remaining two sides.
Which criteria of congruence is used to prove the perpendicular bisector theorem?
SAS (side-angle-side) criteria of congruence are used to prove the perpendicular bisector theorem.

















