Remainder Theorem

Remainder Theorem: Introduction

Just like we divide a number by another number, we can also divide one polynomial by another. 

When we divide a polynomial by a linear polynomial, i.e., a polynomial of degree 1, we apply the remainder theorem to find the remainder. 

Consider an example. The division $9 \div 2$ can be written as:

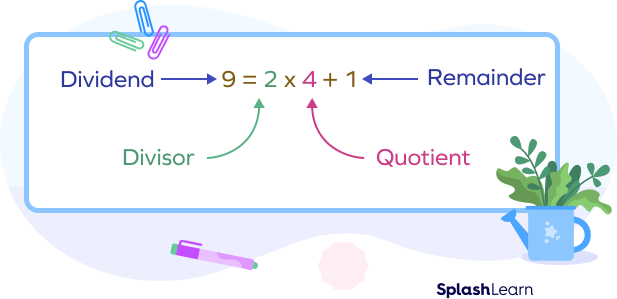
Similarly, if we divide a polynomial f(x) by a linear polynomial g(x) and get a remainder as r(x), we can express it as:

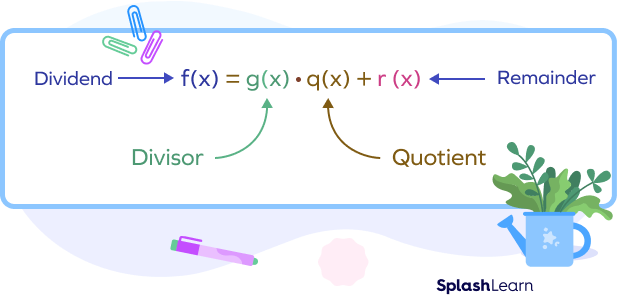
One way of finding the remainder is by long division of polynomials. This gives us the dividend and the quotient. Instead of this, we can use the theorem!

The remainder theorem of polynomials allows us to calculate the remainder of the division of a polynomial without carrying out the steps of long division.

What Is the Remainder Theorem?

The remainder theorem states that when we divide a polynomial p$(x)$ having a degree greater than or equal to 1 by a linear polynomial $(x − a)$, the remainder is given by r$(x) =$ p$(a)$. 

In simple words, if p$(x) = (x − a) q(x) + r(x)$, then $r(x) = p(a)$.

Using this theorem, the remainder of the division of any polynomial by a linear polynomial can be easily calculated.

Note: 

1. The degree of the remainder polynomial is always 1 less than the degree of the divisor polynomial. So, if any polynomial is divided by a linear polynomial (polynomial with degree $= 1$), the remainder is always constant (degree $= 0$).
2. We can say that $(x − a)$ is the divisor of the polynomial P(x) if and only if P(a) $= 0$. So, the theorem is applied to factorize polynomials.

Remainder Theorem: Statement

The remainder theorem states that the remainder when a polynomial p(x) is divided by a linear polynomial $(x − a)$ is p(a).

To find the remainder in a polynomial division, we can follow the given steps:

1. Equate the linear polynomial or the divisor to 0 to find its “zero.” 

So, $(x − a) = 0 \Rightarrow x = a$

2. Substitute $x = a$ in the given polynomial p(x) to find the remainder.

Remainder $= p(a)$

Example: Find the remainder when $p(x) = x^{2} + 4x + 4$ is divided by $(x − 1)$.

Method 1: Long division

Remainder $= 9$

Method 2: Remainder theorem

Here, $x − 1 = 0 \Rightarrow x = 1$

Thus, $a = 1$

Remainder $= p(1) = 1^{2} + 4(1) + 4 = 9$

Remainder Theorem: Proof

By the division algorithm, we can write 

Dividend $=$ (Divisor $\times$ Quotient) $+$ Remainder

Let us assume that q(x) is the quotient and “r” is the remainder when a polynomial p(x) is divided by a linear polynomial $(x – a)$. 

Applying this to polynomial division, we get:

$p(x) = (x − a) q(x) + r$.

If we substitute $x = a$, we get 

$p(a) = (a − a) q(a) + r$

$p(a) = (0) · q(a) + r$

$p(a) = r$

Therefore, the remainder $= p(a)$.

How to Divide a Polynomial by a Non-Zero Polynomial?

The steps are as follows:

1. Arrange the polynomials (dividend and divisor) in decreasing order of their degree.

2. Divide the dividend polynomial’s first term by the divisor’s first term to obtain the first term of the quotient. 

3. Multiply the divisor polynomial by the quotient’s first term.

3. Subtract the resulting product from the dividend to obtain the remainder.

4. This remainder is the dividend now, and the divisor will stay the same. 

5. Repeat the process from the first step again until the degree of the new dividend is less than the degree of the divisor. 

How to Use the Remainder Theorem of Polynomials?

Note the following important points when finding remainder using the remainder theorem.

1. The remainder when p(x) is divided by $(x − a)$ is p(a) 

since $x − a = 0 \Rightarrow x = a$.

2. The remainder when p(x) is divided by $(ax + b)$ is $p( \frac{− b}{a})$ 

since $ax + b = 0 \Rightarrow x = \frac{− b}{a}$.

3. The remainder when p(x) is divided by $(ax − b)$ is $p(\frac{b}{a})$ 

since $ax − b = 0 \Rightarrow x = \frac{b}{a}$.

4. The remainder when p(x) is divided by $bx − a$ is $p(\frac{a}{b})$ 

since $bx − a = 0 \Rightarrow x = \frac{a}{b}$.

Remainder Theorem examples:

Example 1: Find the remainder when you divide $3x^{2} + 2x + 5 by (x + 1)$.

$x − a = x + 1$ 

Here, $a = − 1$.

Remainder $= p(a)$

So $r = p( − 1)$

Substituting $x = − 1$, we get

 $3( − 1)^{2} + 2( − 1) + 5  = 3(1) + 2( − 1) + 5 = 3 − 2 + 5  = 6$.

So, the remainder $= 6$.

Example 2: Find the remainder when you divide $5x^{2} + x + 1$ by $(2x − 1)$.

Put $2x − 1 = 0$

Here, $a = \frac{1}{2}$ and $p(x) = 5x^{2} + x + 1$

Remainder $= p(a) = p(\frac{1}{2}) = 5(\frac{1}{2})^{2} + (\frac{1}{2}) + 1 = \frac{5}{4} + \frac{1}{2} + 1 = \frac{11}{4}$

Remainder Theorem vs. Factor Theorem

Take a look at the following table to understand the difference between remainder theorem and factor theorem.

Remainder Theorem	Factor Theorem
The remainder theorem states that the remainder when p(x) is divided by a linear polynomial of the form $(x − a)$ is given by p(a).	The factor theorem states that $(x − a)$ is a factor of p(x) if and only if f(a) $= 0$.
Remainder theorem is used to find the remainder of the polynomial division only when the divisor polynomial is linear.	Factor theorem helps to decide if a linear polynomial is a factor of the given polynomial or not.

Facts about Remainder Theorem

Here are some facts about the remainder theorem:

• The remainder polynomial is always 1 less degree than the degree of the divisor polynomial.
• Based on this, we can say that when a polynomial is divided by a linear polynomial (whose degree is 1), the remainder is a constant (whose degree is 0).
• The basis of the theorem is that we can find the zero of the divisor linear polynomial by setting it to 0. We say, if $x − a = 0$, then $x = a$. This is why the divisor polynomial plays an important role in the remainder theorem. 

Conclusion

The remainder theorem is important because it helps us divide a polynomial and find the remainder easily. Instead of going through the steps of a long division, we can directly plug in the remainder theorem formula. All we have to do is substitute the right value and solve the polynomial!

Solved Examples

1. If $p(x) = x^{3} + 2x + 1$ is divided by $(x − 1)$, what is the remainder?

Solution: Applying the theorem, we know that the remainder is $r = p(a)$, where p(x) is divided by a linear polynomial of the form $(x − a)$.

Here, $x – 1 = \Rightarrow a = 1$

So, the remainder $= p(1) = 1^{3} + 2(1) + 1$ 

                              $= 1 + 2 + 1$

     $= 4$

2. Find the remainder when $f(x) = 2x^{2} + 4x − 4$ is divided by $(2x − 1)$.

Solution: 

Here, $f(x) = 2x^{2} + 4x − 4$

$2x − 1 = 0 \Rightarrow  a = \frac{1}{2}$

Remainder $= f(\frac{1}{2}) =  2(\frac{1}{2})^{2} + 4(\frac{1}{2}) − 4 = \frac{1}{2} + 2 − 4 =  \frac{− 3}{2}$

3. Check if $(x + 3)$ is a factor of $x^{2}+ 6x + 9$.

Solution: $(x − a)$ is a factor of p(x) if and only if f(a) $= 0$.

$x + 3 = 0 \Rightarrow a = − 3$

$f( − 3) = ( − 3)^{2} + 6( − 3) + 9 = 9 − 18 + 9 = 18 − 18 = 0$

4. If the polynomial $p(x)= 2x^{2} + 3x + 5$ is divided by $(x − 2)$, find the remainder.

Solution. By the theorem, we know that $r = p(a)$ where $x − a = 0$. 

$x − 2 = 0 \Rightarrow a = 2$. 

So, $r = p(a) = p(2)$

$p(2) = 2(4) + 3(2) + 5$

       $= 8 + 6 + 5$

       $= 19$.

Therefore, the remainder is 19. 

5. Find the remainder when you divide $4x^{2} + 3x + 6$ by $(x − 3)$.

Solution. We know that dividend $p(x) = 4x^{2} + 3x + 6$

Remainder $r = p(a)$, where divisor is $x − a$.

Since the divisor is $x − 3 = 0 \Rightarrow a = 3$. 

So $r = p(3)$

$= 4(3)^{2} + 3(3) + 6$

$= 36 + 9 + 6$

$= 51$.

Hence, the remainder $= 51$.

6. Find the remainder when you divide $8x^{2} + 8x + 9$ by $(x − 10)$.

Solution: p(x) $= 8x^{2} + 8x + 9$ 

Remainder = p(a), where divisor is $(x − a)$.

$x − 10 = 0, a = 10$. 

So $r = p(10)$

$= 8(10)^{2} + 8(10) + 9$

$= 800 + 80 + 9$

$= 889$

Hence, the remainder $= 889$.

Practice Problems

Frequently Asked Questions

Related Article Links

• Long multiplication
• Factors
• Order of Operations