Square Numbers: Definition, List, Examples

What Is a Square Number in Math?

A square number is a number obtained when an integer is multiplied by itself. It is also referred to as “a perfect square.” 

We know that the product of a positive integer with a positive integer is always positive. Also, the product of a negative integer and a negative integer is always positive. 

$(+) \times (+) = (+)$

$(-) \times (-) = (+)$

Thus, the square numbers obtained by multiplying an integer with itself are always positive.

Examples of square numbers:

• $5 \times 5 = 25$
• $(-8) \times (-8) = 64$

Square Number: Definition

A square number can be defined as the positive integer obtained by multiplying an integer with itself.

Properties of Square Numbers

• Square numbers always have the digits 0, 1, 4, 5, 6, or 9 as their last digits. 
• A number ending with 2, 3, 7, or 8 cannot be a square number.
• A square number always has an even number of zeros at the end. Therefore, a number is not a square if it has an odd number of zeros as the last digits. For example, the numbers 900 and 4900 are square numbers while 20, 360, and 480 are not squares.
• The square of a number ends with 1 when the last digit of an integer is either 1 or 9. 
• The square number of an integer ends with 6 if its last digit is either 4 or 6. 
• The square number of an even integer is always an even integer, while the square of an odd number is always an odd number. 
• Square numbers are always positive. 
• If a number’s square root is a fraction or a decimal number, it is not a perfect square number. For instance, $\sqrt{0.25} = 0.5$, hence 0.25 is not a square number.

List of Square Numbers (1 to 100)

Here is a list of all of the square numbers from 1 to 100.

Number	Square	Number	Square	Number	Square	Number	Square
1	1	26	676	51	2601	76	5776
2	4	27	729	52	2704	77	5929
3	9	28	784	53	2809	78	6084
4	16	29	841	54	2916	79	6241
5	25	30	300	55	3025	80	6400
6	36	31	961	56	3136	81	6561
7	49	32	1024	57	3249	82	6724
8	64	33	1089	58	3364	83	6889
9	81	34	1156	59	3481	84	7056
10	100	35	1225	60	3600	85	7225
11	121	36	1296	61	3721	86	7396
12	144	37	1369	62	3844	87	7569
13	169	38	1444	63	3969	88	7744
14	196	39	1521	64	4096	89	7921
15	225	40	1600	65	4225	90	8100
16	256	41	1681	66	4356	91	8281
17	289	42	1764	67	4489	92	8464
18	324	43	1849	68	4624	93	8649
19	361	44	1936	69	4761	94	8836
20	400	45	2025	70	4900	95	9025
21	441	46	2116	71	5041	96	9216
22	484	47	2209	72	5184	97	9409
23	529	48	2304	73	5329	98	9604
24	576	49	2401	74	5476	99	9801
25	625	50	2500	75	5625	100	10000

Two-digit Square Numbers

There are only six “two-digit square numbers.” 

$4 \times 4 = 16$

$5 \times 5 = 25$

$6 \times 6 = 36$

$7 \times 7 = 49$

$8 \times 8 = 64$

$9 \times 9 = 81$

Three-digit Square Numbers

There are only 22 three-digit square numbers.

100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 

441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961.

Odd and Even Square Numbers

The meaning of a square number is simple; when we multiply a number by itself we get a square number. These square numbers can be divided into two types: 

• Even square numbers: The square of any even number is always an even square number. For example, $2^{2} = 4,\; 6^{2} = 36$
• Odd square numbers: The square of any odd number is always an odd square number. For example, $3^{2} = 9,\; 7^{2} = 49$

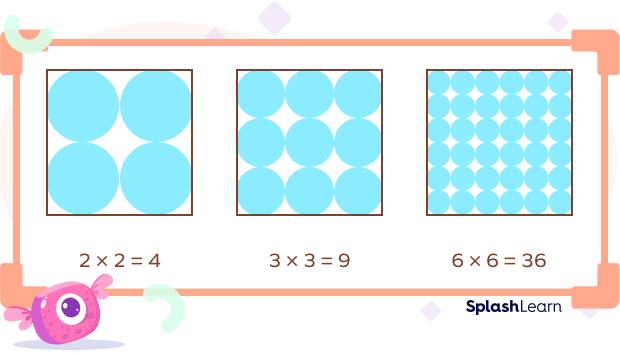
Square Numbers and Multiplication Arrays

The name “square” comes from the fact that all square numbers can be represented using a square-shaped array. They fill a square.

The following figure has the number of balls arranged in a square. We can see that the number of balls that fill a square is a square number. 

If we take 4 balls, we can see that they can be arranged in an array to form a square shape. Same goes for the square numbers 9, 36, etc.

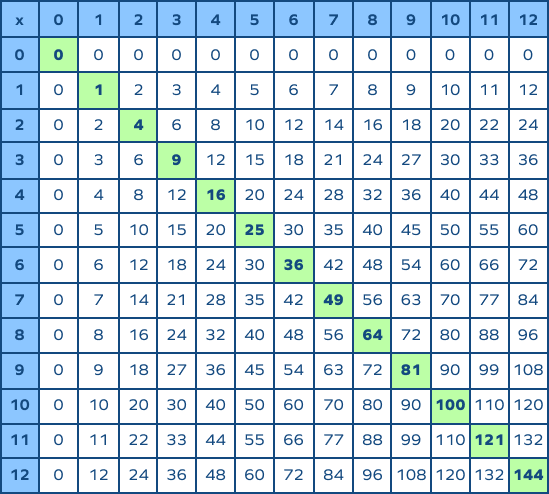
Square Numbers on Multiplication Chart

Notice that the square numbers appear diagonally in a multiplication chart.

Facts about Square Numbers

Conclusion

In this article, we learned about square numbers, their properties along with the list of squares from 1 to 100. Let’s solve a few examples and practice problems. 

Solved Examples on Square Numbers

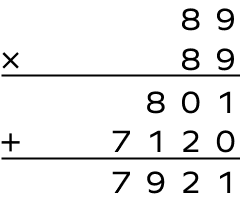
1. Find the square of 89. 

Solution: 

To find the square of the number 89, we need to multiply 89 by 89.

$89^{2} = 89 \times 89$

$89 \times 89 = 7921$

2. Find the square of -25. 

Solution: 

The square of $-\;25$ would be the product of $-\;25$. 

$(\;-\;25)^{2} = (\;-\;25) \times (\;-\;25)$

$(\;-\;25)^{2} = 625$ 

3. Is 113 a square number?

Solution: 

All square numbers end with 0, 1, 4, 5, 6, or 9.

If a number ends with 2, 3, 7, or 8, then it is not a square number.

Practice Problems on Square Numbers

Frequently Asked Questions on Square Numbers