What Is the Surface Area of a Hemisphere?
The surface area of a hemisphere is defined as the area covered by the outer surface of a hemisphere. The surface area of a hemisphere is measured in square units.
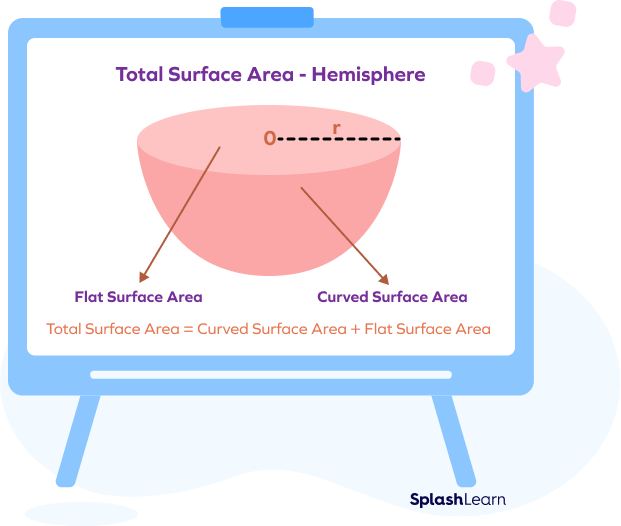
The surface of a hemisphere consists of a flat circular base and curved surface.
A hemisphere is a three-dimensional shape that is half of a sphere. The hemisphere can either be hollow or solid.
A sphere is a three-dimensional shape. It has no edges. If you cut a sphere into exactly two halves by a plane, each half is called a hemisphere. Simply put, the hemisphere is half of a sphere.
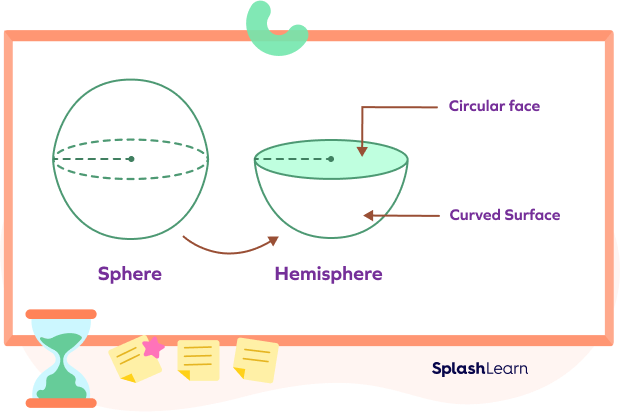
You can see that a hemisphere has one curved surface and 1 flat surface.
Recommended Games
Surface Area of a Hemisphere: Formulas
| Description | Formula |
|---|---|
| Base Area of Hemisphere | B $= \pi r^{2}$ |
| Curved Surface Area of Hemisphere | CSA $= 2\pi r^{2}$ |
| Total Surface Area of Hemisphere | TSA $= 3\pi r^{2}$ |
Recommended Worksheets
Curved Surface Area of Hemisphere
To calculate the total surface area of the sphere, we use the formula:
Total Surface Area of the sphere Formula = 4πr2
The curved region of the hemisphere is exactly half of the curved region of the sphere.
Surface area of half a sphere = Curved Surface Area of a Hemisphere
So, we simply need to divide the total surface area of the sphere by 2 to get the curved surface area of the hemisphere.
Curved Surface Area of Hemisphere Formula = 2πr2
where ‘r’ is the radius of the hemisphere
Base Area of Hemisphere
The base of the hemisphere is a flat circular shape.
Area of circle = πr2
Area of the circular base of a hemisphere = πr2
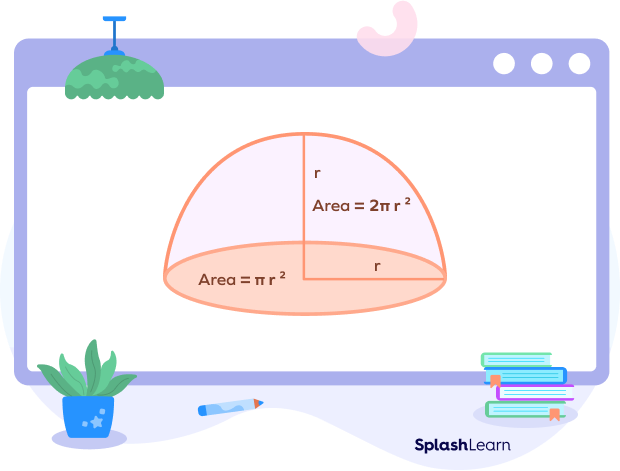
Total Surface Area of Hemisphere
The total surface area of the hemisphere is defined as the sum of the space occupied by the curved area and the flat surface area (or the base area) of the hemisphere.
Thus, the total surface area of the hemisphere can be calculated using the following formula:
Total surface area of a hemisphere = Curved Surface Area + Base Area
TSA = 2πr2 + r2
TSA = 3πr2
How to Find the Surface Area of a Hemisphere
Depending on whether we are calculating the curved surface area or the total surface area of a hemisphere, we have to choose the correct formulas.
Lets see steps of how to find curved surface area and total surface area of hemisphere.
Curved Surface Area of Hemisphere
Curved Surface Area of the hemisphere = 2πr2
Example: Find the curved surface area of a hemisphere with radius 2 units.
Note down the radius (r) of the hemisphere.
r= 2 units
Substitute the value in the formula CSA = 2πr2
CSA = 2πr2
CSA $= 2 \times \frac{22}{7} 2^{2}$
CSA = 25.14 square units
Total Surface Area of Hemisphere
The formula to calculate the total surface area (TSA) of a hemisphere with radius ‘r’ is given as, TSA of hemisphere = 3πr2
Example: Find the curved surface area of a hemisphere with radius 7 units.
r = 7 units
TSA of hemisphere = 3πr2
TSA of hemisphere $= 3 \times \frac{22}{7} 7^{2}$
TSA of hemisphere = 462 square units
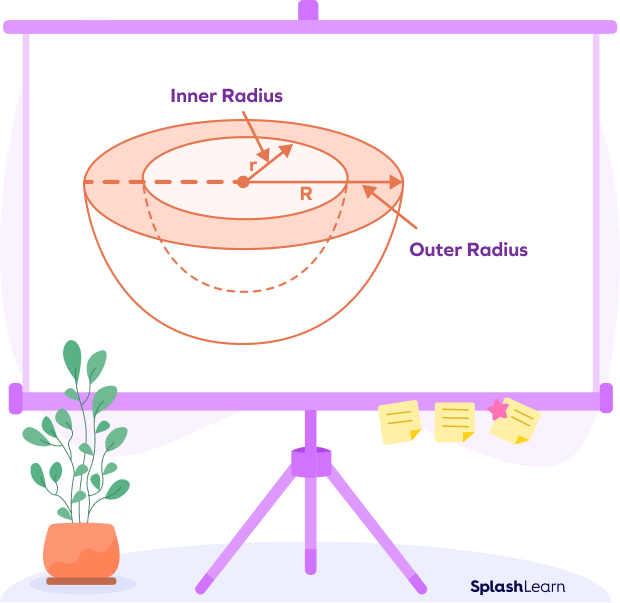
Surface Area of Hollow Hemisphere
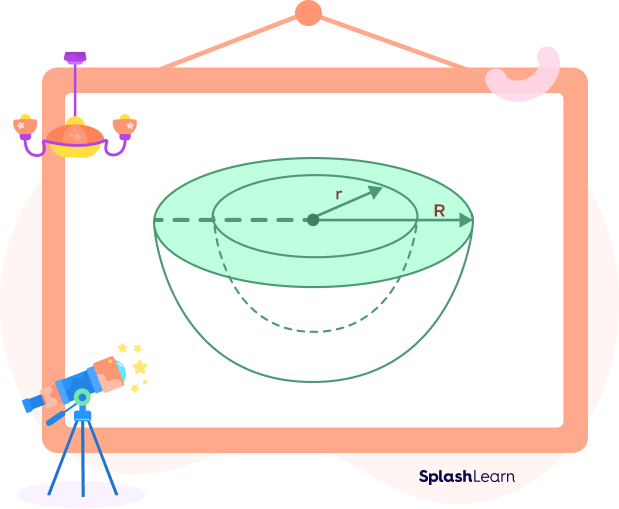
A hollow hemisphere is a three-dimensional shape whose base looks like a flat ring. It is hollow on the inside.
A hollow hemisphere’s inner and outer circular bases can each have a different radius.
Because of this, a hollow hemisphere has two curved surfaces, such as an inner and outer curve. A hemisphere’s thickness is determined by the difference between its inner and outer radii.
Surface Area of a Hollow Hemisphere Formula and Derivation
If ‘r’ is the inner radius (radius of the inside circular base), and ‘R’ is the outer radius (radius of the outside circular base), we can derive the following formulas.
- The curved surface area of the outer hemisphere = 2πR2
- The curved surface area of the inner hemisphere = 2πr2
Observing the figure given below, we can see that a ring is formed at the base of a hollow hemisphere.
Area of the ring = Area of outer hemisphere – area of inner hemisphere = (R2 – r2)
So, the Total surface area of the hollow hemisphere can be calculated as
TSA of a hollow hemisphere = 2πR2 + 2πr2 + π(R2 – r2)
TSA of hollow hemisphere = 2π(R2 + r2) + (R2 – r2)
TSA of hollow hemisphere = 3πR2 + r2
Facts about Surface Area of Hemisphere
- The prefix “hemi” has a Greek origin and it means “half.”
- A hemisphere is half of the sphere.
Conclusion
In this article, we learnt about the surface area of the hemisphere and hollow hemisphere. We also learnt the formulas for the same. Let’s use this knowledge to solve some examples and practice problems.
Solved Examples on Surface Area of a Hemisphere
Example 1: Find the surface area of the hemisphere if its radius is 14 units?
Solution:
The radius of the hemisphere is 14 units.
We know that the total surface area of the hemisphere = 3πr2
Thus, TSA $= 3\times \frac{22}{7} \times 14 \times 14$
$= 3 \times 22 \times 2 \times 14$
$= 1848$ square units.
Therefore, the total surface area of the hemisphere is 1848 square units.
Example 2: Find the surface area of a hollow hemisphere whose outer radius measures 20 units and inner radius is 10 units. (Use π = 3.14)
Solution:
The outer radius (R) of the hemisphere = 20 units
The inner radius (r) = 10 units
Substituting the value of R and r in the formula, we get
TSA of hollow hemisphere = 3πR2 + r2
= [3π × (20)2] + [π × (10)2]
= (3 × 3.14 × 400) + (3.14 × 100)
= 3768 + 314
= 4082 square units
Therefore, the surface area of the hollow hemisphere = 4082 square units.
Example 3: Calculate the radius of a hemisphere if its curved surface area is 500 sq. in.
Solution:
A = 500
Curved surface area of hemisphere A = 2πr2
A = 2πr2
$r^{2} = \frac{A}{2\pi}$
$r^{2} = \frac{500}{2 \times 3.14}$
$r^{2} = \frac{250}{3.14}$
r2 = 79.617
r = $\sqrt{79.617}$
r = 8.922
Thus, the radius of the hemisphere = 8.922 in.
Practice problems on Surface Area of a Hemisphere
Surface Area of a Hemisphere - Definition, Formula, Examples
Curved surface area of the hemisphere with radius “r” is equal to __________.
The curved surface area of a hemisphere $= \frac{Surface\; area\; of\; a \;sphere}{2} = \frac{4\pi r^{2}}{2} = 2\pi r^{2}$
Total surface area of a hemisphere of radius “r” is equal to __________.
Total surface area of a hemisphere = Curved surface area + Base area
$= 2\pi r^{2} + \pi r^{2}$
$= 3\pi r^{2}$
Total surface area of hollow hemisphere =
If 'r' is the radius of the internal hemisphere, and 'R' is the radius of the external hemisphere,
TSA of hollow hemisphere can be calculated using the formula, TSA $= 3\pi R^{2} + \pi r^{2}$
Frequently asked questions about Surface Area of a Hemisphere
Is the hemisphere a polyhedron?
No, a polyhedron is a three-dimensional solid made up of polygons. A hemisphere is not a polyhedron as a hemisphere has one circular base and one curved surface.
What are the geometric properties of a hemisphere?
- A hemisphere has only one curved surface area.
- It has one circular base.
- A hemisphere has no vertices.
- A hemisphere has one curved edge.
- Hemisphere is not a polyhedron since polyhedrons are formed by polygons.
How do you find the curved surface area of a hemisphere with the diameter given?
We know that curved surface area of the hemisphere can be calculated using the formula:
Curved Surface area of the hemisphere $= 2\pi r^{2}$, where ‘r’ is the radius of the hemisphere.
We also know that radius is half the diameter.
$r = \frac{d}{2}$
Thus, we can use this value to solve the problem.
What is the lateral surface area of a hemisphere?
The lateral surface area is nothing but the curved surface area of the hemisphere. The curved surface area of the hemisphere is calculated using the formula
Curved surface area of the hemisphere $= 2\pi r^{2}$
where ‘r’ is the radius of the hemisphere.
What is the formula for the surface area of a hemisphere?
Total surface area of a hemisphere $= 3\pi r^{2}$, where ‘r’ is the radius of the hemisphere.




































