Transitive Property: Introduction
Transitive property refers to a property by which if number a is related to the number b by a certain rule, and the number b is related to the number c by the same rule, then we can definitely say that the number a is related to the number c by the same rule.
Let’s understand this using an example. Suppose Alex has $\$10$ in the piggy bank. Joy has the same amount in the piggy bank as Alex. George has the same amount of money as Joy. What does this imply? It’s simple! It means Alex and George have the same amount of money, $\$10$.

Recommended Games
Transitive Property: Definition
Let us understand transitive property meaning in depth.
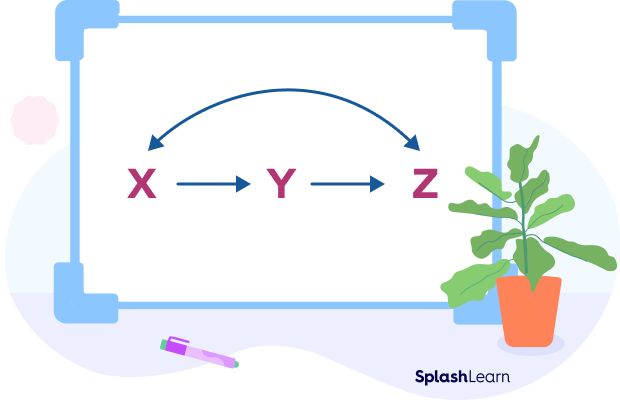
The word transitive means to transfer. If x, y and z are any three quantities, and if x is related to y by some rule and y is related to z by the same rule, then we can conclude that x and y are related to each other by the same rule. This property is known as the transitive property of equality.
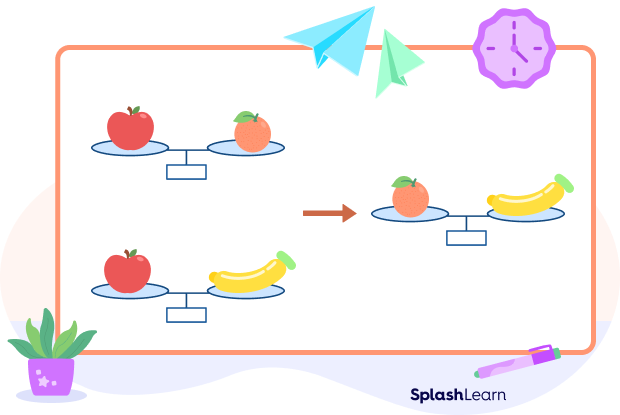
Let’s take another example. Suppose an apple weighs the same as an orange. An orange weighs the same as a banana. Then we can say that the apple weighs the same as the banana.
Recommended Worksheets
What Is the Transitive Property of Equality?
The transitive property of equality states that:
If $\text{x} = \text{y}$ and $\text{y} = \text{z}$, then $\text{x} = \text{z}$.
The definition of the transitive property of equality by Euclid is simple. He defines it as “things which are equal to the same thing are also equal to each other.”

Let’s also explore two properties of equality that are closely related to the transitive property of equality.
Reflexive Property of Equality
The reflexive property states that $x = x$ for any real number $x$. Thus, any variable is always equal to itself.
Symmetric Property of Equality
According to the symmetric property of equality, if $x = y$, then $y = x$.
Thus, the order in which two variables are equated, LHS or RHS, does not matter.
Transitive Property of Inequality
Transitive property applies to equality as well as inequality and it states that, if we have three real numbers a, b, and c such that, $a \lt b$ and $b \lt c$, then $a \gt c$.
Transitive property can also be applied to other inequalities, such $as \gt$, $\le$ and $\ge$.
For example, if we have a number $p \le 15$ and $15 \le q$, then $p \le q$.
Let us look at another example. Roy is shorter than Jim. Jim is shorter than Mike. According to the transitive property of inequality, we can say that Roy is shorter than Mike.

Transitive Property of Congruence
The definition of transitive property of congruence can be given as:
If two shapes are congruent to a third shape, then all the shapes are congruent among each other.
Let us consider three triangles, $\Delta ABC, \Delta PQR$, and $\Delta MNO$.
The transitive property of congruence is given as follows:
If $\Delta ABC \Cong \Delta PQR$ and $\Delta PQR \Cong \Delta MNO$, then $\Delta ABC \Cong \Delta MNO$
It clearly means that the triangle ABC is congruent to triangle PQR, and triangle PQR is congruent to triangle MNO, then we can say that the triangle ABC is congruent to the triangle MNO.
General Formula of Transitive Property
The formula of transitive property of equality is given as follows:
If $a = b$ and $b = c$, then $a = c$.
For any real numbers, a, b and c, the transitive property of inequalities states that:
If $a \lt b$ and $b \lt c$, then $a \lt c$.
If $a \gt b$ and $b \gt c$, then $a \gt c$.
If $a \le b$ and $b \le c$, then $a \le c$.
If $a \ge b$ and $b \ge c$, then $a \ge c$.
When Do We Use Transitive Property?
The transitive property in geometry is used when we are dealing with quantities following the same rule. It uses a comparison mechanism to find the values of variables. Transitive property can be applied to numbers, algebraic expressions, congruent angles, triangles, etc. It connects multiple equal quantities and thus has applications in arithmetic, logic, and algebra.
Transitive Property of Angles
According to the transitive property of congruence, if $\angle A$ is congruent to $\angle B; \angle B$ is congruent to $\angle C$, then $\angle A$ is congruent to $\angle C$.
Example: If we have angles a and b such that $\angle A = \angle B$ and $\angle B = \angle C$ and $\angle A = 60^{\circ}$, then by the transitive property of angles, we get $\angle C = 60^{\circ}$.
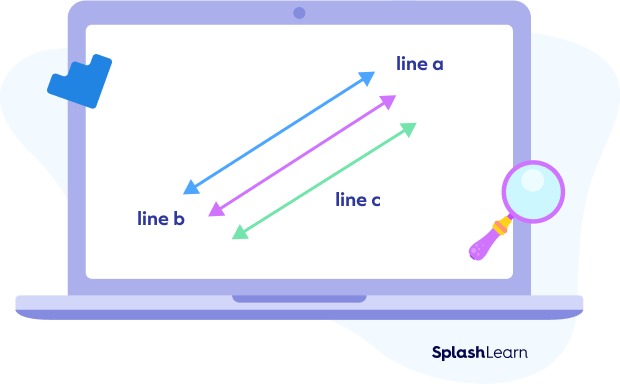
Transitive Property of Parallel Lines
If line a is parallel to line b, and line b is parallel to line c, then we can say that line a is also parallel to line c.
Transitive Property of Inequality of Real Numbers
In mathematics, inequalities are just as important as equalities. We know that the transitive property also applies to inequalities such that:
If $a \lt b$ and $b \lt c$, then $a \lt c$.
To visualize this property, consider three people whose weights are unknown. It is known that Mike is shorter than Oscar and that Oscar is shorter than David. Logic allows the conclusion that Mike is also shorter than David.
This property works in the reverse order as well: $a \gt b$ and $b \gt c$ then $a \gt c$.
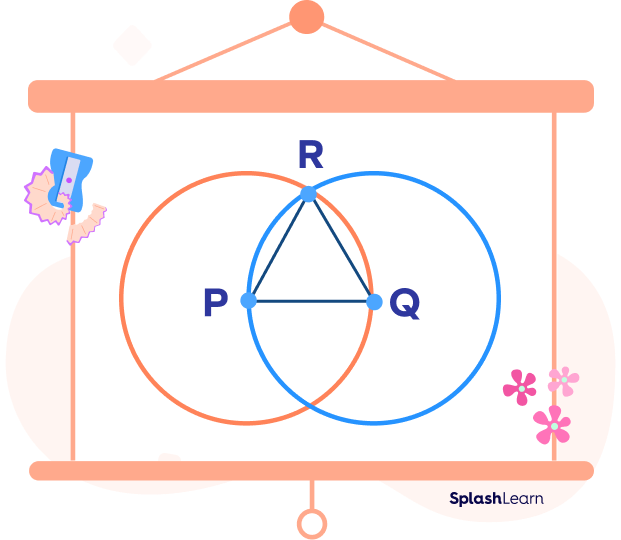
Construction of Equilateral Triangle using Transitive Property
Transitive property is an axiom, i.e., a statement that is self-evident and accepted without proof. The construction of an equilateral triangle using a ruler and a compass is a popular example where transitive property is used.
Step 1: Draw line segment PQ with any measurement.
Step 2: Draw one circle keeping center P and radius PQ. Draw another circle with the center Q and radius QP.
Step 3: Name the point of intersection of two circles as R. Join PQR to form a triangle.
As we know, PQ and PR are the radii of the circle with P as the center.
$PQ = PR$ (see red circle).
$PQ and QR$ are the radii of the circle with Q as the center.
$PQ = QR$ (see blue circle).
Since $PQ = PR$ and $PQ = QR$, we can say $PR = QR$ according to the transitive property of equality. Therefore, all three lines are equal to each other making PQR an equilateral triangle.
Fun Facts!
- The transitive property of equality : If $x = y$ and $y = z$, then $x = z$
- This property can be applied to algebraic expressions, numbers, and various geometrical concepts like congruent angles, triangles, etc.
Conclusion
In this article, we learned about transitive property. We got to know about the transitive property of equality and inequality. We also discussed formulas and now we can solve practice problems to better understand transitive property.
Solved Examples
1. What is the value of $\text{x}$, if $x = y$ and $y = 5$?
Solution:
By using the transitive property, if $x = y$ and $y = 5$, then $x = 5$.
Therefore, the value of $x$ is $5$.
2. What is the value of t, if $t + 3 = u$ and $u = 9$?
Solution:
By using the transitive property, if $t + 3 = u$ and $u = 9$, then
$t + 3 = 9$
$\Rightarrow t = 9 − 3$
$\Rightarrow t = 9 − 3$
$\Rightarrow t = 6$
Therefore, the value of t is 6.
3. Find the value of $\angle R$, if $\angle P = \angle Q$ and $\angle Q = \angle R$, where $\angle P = 120^{\circ}$.
Solution:
By using the transitive property of angles,
If $\angle P = \angle Q$ and $\angle Q = \angle R$ then automatically, $\angle P = \angle R$.
Therefore, the value of $\angle P = \angle R = 120^{\circ}$.
4. Find the value of $\angle R$, if $\angle P + 60^{\circ} = \angle Q$ and $\angle Q = \angle R$, where $\angle P = 120^{\circ}$.
Solution:
By using the transitive property of angles,
If $\angle P + 60^{\circ} = \angle Q$ and $\angle Q = \angle R$ then automatically, $\angle P + 60^{\circ} = \angle R$.
Therefore, the value of $\angle P + 60^{\circ} = \angle R$
Or $120^{\circ} + + 60^{\circ} =\angle R$
Or $\angle R = 180^{\circ}$
Therefore, the value of $\angle R = 180^{\circ}$.
5. Assume that $3x + 3 = b$ and $b = 5x − 1$. What is the value of b?
Solution:
In this transitive property example the solution uses the transitive property of equalities to set $3x + 3$ equal to $5x − 1$.
Thus, $3x + 3 = 5x − 1$. Solving for x results in $− 2x = − 4$; thus $x = 4/2= 2$.
Hence, the value of $x$ is $2$.
Practice Problems
Transitive Property
What is the value of a, if $a = b$ and $b = 7$?
By using the transitive property, if $a = b$ and $b = 7$, then $a = 7$.
Therefore, the value of a is $7$.
What is the value of t, if $m + 2 = n$ and $n = 3$?
By using the transitive property, if $m + 2 = n$ and $n=3$, then
$\Rightarrow m + 2 = n$
$\Rightarrow m= n$ $-$ $2$
$\Rightarrow m = 3$ $-$ $2$
$\Rightarrow m = 1$
The value of m is 1.
What is the value of $\angle A$, if $\angle B = \angle C$ and $\angle C = \angle A$, and $\angle B = 45^{\circ}$.
By using the transitive property of angles,
If $\angle B = \angle C$ and $\angle C = \angle A$ then automatically, $\angle B = \angle A$.
Therefore, the value of $\angle B = \angle A = 45^{\circ}$.
At what value of $\angle A$, if $\angle B + 45^{\circ} = \angle C$ and $\angle C = \angle A$, where $\angle B = 45^{\circ}$.
If $\angle B + 45^{\circ} = \angle C$ and $\angle C = \angle A$ then automatically, $\angle B + 45^{\circ} = \angle A$.
Therefore, the value of $\angle B + 60^{\circ} = \angle A$
Or $45^{\circ} + + 45^{\circ} = \angle A$
Or $\angle A = 90^{\circ}$
Therefore, the value of $\angle A = 90^{\circ}$.
Assume that $3x + 3 = b$ and $b = 5x$ $-$ 1$. What is the value of b?
In this transitive property example the solution uses the transitive property of equalities to set $5x + 7$ equal to $4x$ $-$ $9$.
Thus, $5x + 7 = 4x$ $-$ $9$. Solving for x results in
$5x + 7 = 4x$ $-$ $9$
Or $5x$ $-$ $4x = $$-$$9$ $-$$7$
Or $x = $$-$ $16$
The value of x is $-16$.
Frequently Asked Questions
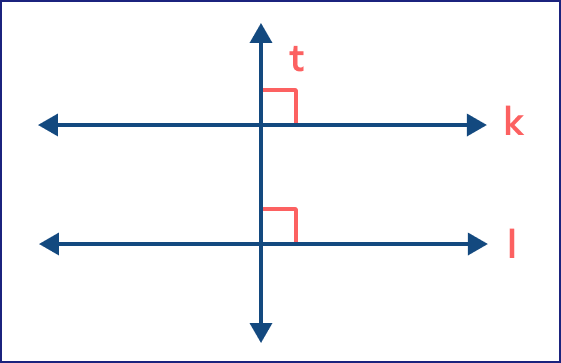
Do perpendicular lines follow transitive property?
No. If one line is perpendicular to the second line and the second line is perpendicular to the third line, then the first line becomes parallel to the third line. Thus, transitive property fails.
What is reflexive property?
The reflexive property states that for every real number $a$, $a = a$.
What is the symmetric property?
The symmetric property states that for all real numbers a and b,
if $a = b$ then $b = a$.
What is the substitution property?
If $a = b$, then a may be replaced by b in any equation or expression.
Where do we use the transitive property?
The transitive property is generally used, when we have multiple quantities, which have the same category and are related by the same rule.