Number Properties – Introduction
Number properties are certain rules that can be applied and characteristics that numbers follow when we perform arithmetic operations on them. In mathematics, we use numbers to express mathematical facts and ideas logically. But what are number properties? Why do you need to learn them? We know that everything around us has certain properties, such as shape, size, weight, etc. Like these things, numbers also have some properties. Knowing the properties will help you solve equations easily.
Come, let’s explore the properties of numbers in detail.
Recommended Games
What Are Number Properties in Math?
Number properties refer to the properties that help to express the basic characteristics or features of real numbers. There are four basic properties in math:
- Commutative Property
- Associative Property
- Distributive Property
- Identity Property
We apply these properties while doing addition and multiplication operations.
Recommended Worksheets
Commutative Property
To commute means to move from one place to another. Let’s understand how it relates to the number properties.
Commutative Property of Addition
This property says that when we add two numbers, the order in which we add the numbers makes no difference to the answer.
Example:
Suppose we have to add 3 and 5.
We can write $3 + 5 = 8$.
Similarly, we can also write it as $5 + 3 = 8$.
Thus,
$3 + 5 = 5 + 3 = 8$
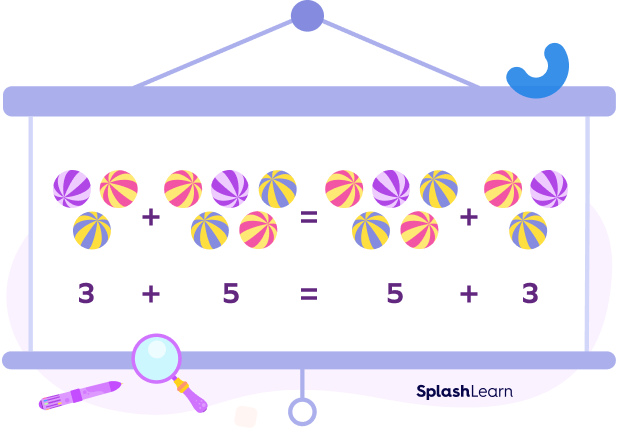
Hence, the commutative property of addition for any two real numbers a and b is given as:
$a + b = b + a$
Commutative Property of Multiplication
This property says that when we multiply two numbers, the order in which we multiply the numbers makes no difference to the answer.
Example:
Let’s multiply 4 and 5. We get $4 \times 5 = 20$. Now, if we reverse the order of the numbers and multiply, we get $5 \times 4 = 20$.
Thus,

Hence, the commutative property of multiplication for any two real numbers a and b is given as:
$a \times b = b \times a$
Associative Property
The word “associative” refers to combining or collaborating. Let’s understand the property.
Associative Property of Addition
This property says that when we add three or more numbers, the order in which the numbers are grouped has no impact on the sum.
Example:
Suppose we have to add 3, 4, and 5. We first group 3 and 4 as $(3 + 4)$ and add the sum to 5. Next, we take 3 and add it to the group of 4 and 5 as $(4 + 5)$. We get
$(3 + 4) + 5 = 3 + (4 + 5) = 12$.

Hence, the associative property of addition for three real numbers a, b, and c is:
$(a + b) + c = a + (b + c)$
Associative Property of Multiplication
This property says that when we multiply three or more numbers, the order in which the numbers are grouped has no impact on the product.
Example:
We take the numbers 2, 3, and 5. We first group 2 and 3 as $(2 \times 3)$ and multiply the product by 5.
We get $(2 \times 3) \times 5 = 6 \times 5 = 30$.
Next, we group 3 and 5 as $(3 \times 5)$ and multiply by 2.
So, 2 $(3 \times 5) = 2 \times 15 = 30$.
Thus,
$(2 \times 3) \times 5 = 2 \times (3 \times 5) = 30$.
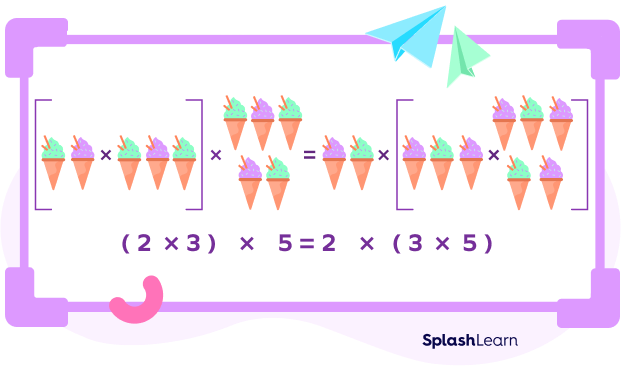
Hence, the associative property of multiplication for three real numbers a, b, and c is:
$(a \times b) \times c = a \times (b \times c)$
Identity Property of Addition
Identity Property
This property says that when we add 0 to any number, the sum is equal to the number itself. We call 0 the additive identity.
Example:
Let’s take the 5 and add 0 to it. We get $5 + 0 = 5$ or $0 + 5 = 5$.
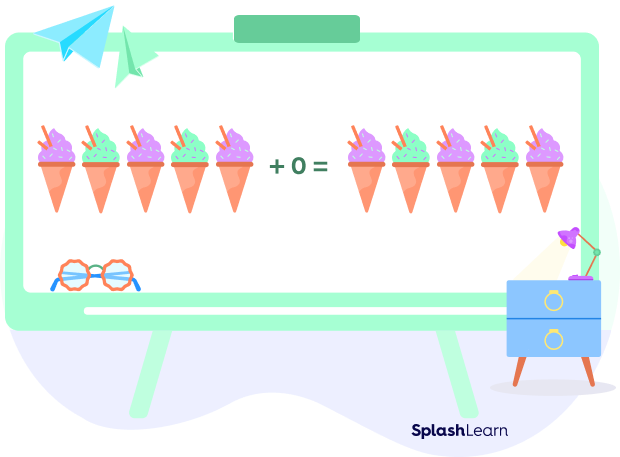
Hence, the identity property of addition for any real number a is:
$a + 0 = 0 + a = a$
Identity Property of Multiplication
This property says that when we multiply any number by 1, the product is equal to the number itself. We call 1 the multiplicative identity.
Example:
Let’s take the 4 and multiply it by 1.
We get
$4 \times 1 = 4$ or $1 \times 4 = 4$.
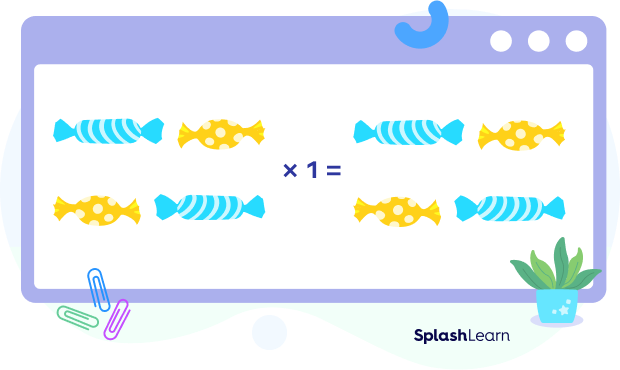
Hence, the identity property of multiplication for any real number a is:
$a \times 1 = 1 \times a = a$
Distributive Property of Multiplication Over Addition
The distributive property says that when you multiply a number by the sum of two or more addends, the product is the same as the result of the multiplication of the number by each of the addends individually and then adding the products. This property specifies that multiplication distributes over addition.
Example:
Let’s multiply 3 by the sum of 4 and 5. We get $3 \times (4 + 5) = 27$. Now we multiply 3 by 4 and 5 individually and then add the products. We get $(3 \times 4) + (3 \times 5) = 12 + 15 = 27$.
Thus, $3 \times (4 + 5) = (3 \times 4) + (3 \times 5) = 27$
Now, let’s consider the expression $(2 + 3) \times 7$. We get $(2 + 3) \times 7 = 5 \times 7 = 35$. When we multiply 2 and 3 individually with 7 and add the products, we get $2 \times 7 + 3 \times 7 = 14 + 21 = 35$.
Thus, $(2 + 3) \times 7 = (2 \times 7) + (3 \times 7) = 35$
These two examples of math properties show how we can distribute an expression for easy computation. For $a \times (b + c)$, we can expand the expression using the distributive property as:

For $(b + c) \times a$, we can expand the expression using the distributive property as:
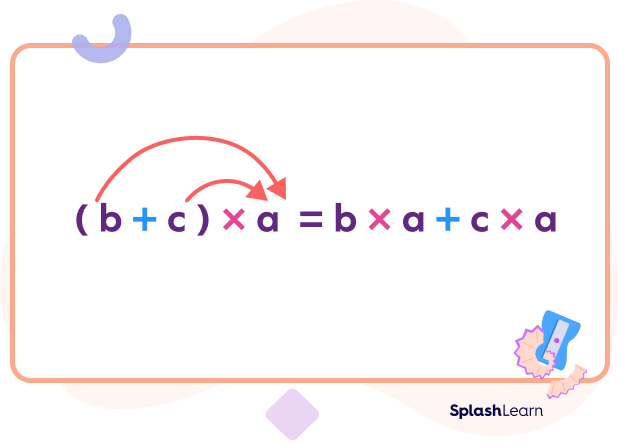
Hence, the distributive property of multiplication over addition for three real numbers a, b, and c is:
$a \times (b + c) = a \times b + a \times c$
Formula Chart of Basic Number Properties
Here’s a list of math properties shown in the chart below. It includes the formula for the four basic math properties of operations discussed above.

Fun Facts!
- There is just one version of the distributive property for multiplication and addition. It doesn’t have two individual rules for addition and multiplication.
- The commutative property derives its name from the commute, which means to travel or move around.
- The associative property derives its name from the term associate.
- The identity property of addition is also known as the zero property of addition.
Conclusion
Number properties tell us how math operations relate to one another. By using the 4 properties of math mentioned above, you can simplify computation and strengthen your base for learning higher mathematical concepts.
Solved Examples of Number Properties
1. Identify the number property used in the given equation.
$(12 \times 9) \times 4 = 12 \times( 9 \times 4)$
Solution:
The property used is the associative property of multiplication,
$(a \times b) \times c = a \times (b \times c)$
The product is not affected by the way we group the numbers.
2. Is $3yz = 3zy$?
Solution:
Yes, $3yz = 3zy$.
By the commutative property of multiplication, we have $a \times b = b \times a$
We can say that $3yz = 3zy$.
3. By the commutative property of addition, $n + 3 =$ ?
Solution:
By the commutative property of addition, we have
$a + b = b + a$; for any real numbers a and b
Thus, $n + 3 = 3 + n$
The order of numbers does not affect the sum.
4. If $4m \times 1 = 20$, find the value of m using the identity property of multiplication.
Solution: The given expression is $4m \times 1 = 20$.
As per the identity property of multiplication, $a \times 1 = a$
So, $4m = 20$
$m = \frac{20}{4}$
$m = 5$.
Hence, the value of m is 5.
5. Solve the given expression using the distributive property.
$6 \times (5 + 8)$
Solution: The distributive property for three real numbers a, b, and c is
$a \times (b + c) = a \times b + a \times c$.
Let’s consider $a = 6, b = 5$, and $c = 8$, and substitute the values in the equation
$a \times (b + c) = a \times b + a \times c$.
We get $6 \times (5 + 8) = 6 \times 5 + 6 \times 8 = 30 + 48 = 78$.
So, $6 \times (5 + 8) = 78$.
Practice Problems of Number Properties
Number Properties
Which property is used in the image below?
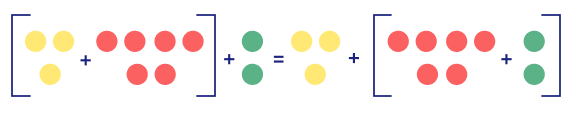
If we consider $a = 3$ yellow balls, $b = 6$ red balls, and $c = 2$ green balls, and substitute them in the equation, we get: $(a + b) + c = a + (b + c)$. This is the associative property of addition.
Which of the following is an example of identity property of addition?
The identity property of addition is $a + 0 = a$. When we substitute 20 as the value of a in this expression, we get $20 + 0 = 20$.
Select the number property that the given expression illustrates. $yz \times 1 = yz$
The identity property of multiplication is $a \times 1 = a$. If we consider $a = yz$, we can express this property as $yz \times 1 = yz$.
Which expression is equal to $(7 \times 3) \times 9$?
According to the associative property of multiplication, $(a \times b) \times c = a \times (b \times c)$.
Thus, $(7 \times 3) \times 9 = 7 \times (3 \times 9)$.
If you expand $5 \times (9 + 1)$ using the distributive property, which expression will you get?
The distributive property of multiplication over addition is $a \times (b + c) = a \times b + a \times c$.
By substituting $a = 5$, $b = 9$, and $c = 1$, we get the expression $5 \times (9 +1) = 5 \times 9 + 5 \times 1$.
Frequently Asked Questions of Number Properties
What are real numbers?
Real numbers include fractions, positive integers, negative integers, and irrational numbers.
Do decimal numbers follow the math properties mentioned above?
Yes, decimal numbers follow the math properties mentioned above.
Can we use the commutative property for subtraction?
No, we can’t. This is because the commutative property doesn’t hold for subtraction.
Is $-1$ a multiplicative identity?
No, $− 1$ isn’t a multiplicative identity. This is because if we multiply any real number by $− 1$, the sign of the number changes. For example, $9 \times − 1 = − 9$. Also, $− 9 \times − 1 = 9$.
What is the additive identity of $− 1?
The additive identity of $− 1$ is 0.




































