Properties of Multiplication – Definition, Examples, Facts, FAQs

What Are the Properties of Multiplication?

The properties of multiplication are certain rules or formulas that help in simplifying the expressions involving multiplication.

We know that multiplication is defined as repeated addition. 

For example, $12 \times 6$ is 12 added to itself 6 times.

$12 \times 6= 12 + 12 + 12 + 12 + 12 + 12$

             $= 72$

The five basic properties of multiplication are: 

• Commutative property
• Associative property
• Distributive property
• Identity property
• Zero property

Properties of Multiplication

Properties of Multiplication
Commutative Property	$a \times b = b \times a$
Associative Property	$a \times (b \times c) = a \times (b \times c)$
Distributive Property	$a \times (b + c) = (a \times b) + (a \times c)$ $a \times (b\;-\;c) = (a \times b) \;-\; (a \times c)$
Identity Property	$a \times 1 = 1$
Zero Property	$a \times 0 = 0$

Commutative Property of Multiplication

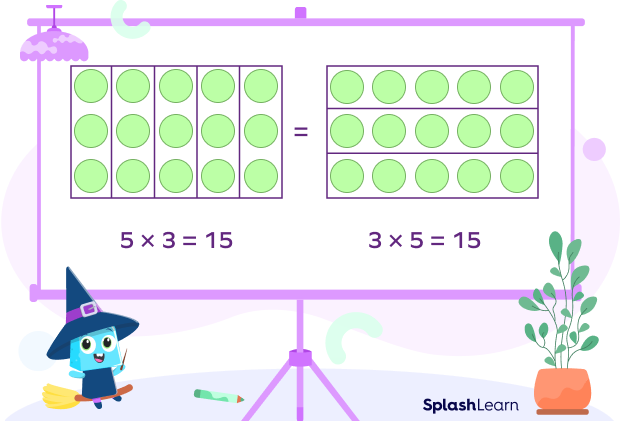
The commutative property of multiplication states that the multiplication of two numbers remains the same even if the order of numbers is changed. Changing the order of multiplication doesn’t change the product.

Example 1: Let’s multiply 3 by 5.

$3 \times 5 = 3 + 3 + 3 + 3 + 3 = 15$

Now on reversing the order of multiplication, we get 

$5 \times 3 = 5 + 5 + 5 = 15$ 

The answer is the same even after changing the order of the numbers. Thus, the multiplication is commutative.

Look at the same example using a multiplication array.

Associative Property of Multiplication

Associative property of multiplication states that if we want to multiply any three numbers together, the answer will always be the same irrespective of the order in which we multiply the numbers.

$a \times (b \times c)=(a \times b) \times c$

Example: 

$2 \times (5 \times 4)=2 \times 20 = 40$

$(2 \times 5) \times 4=10 \times 4 = 40$

As in both cases, the answer we get is the same, irrespective of how the numbers are grouped. Hence, multiplication is associative.

Distributive Property of Multiplication

The distributive property of multiplication states that multiplication can be distributed over addition as well as subtraction. This property helps us solve the expressions with brackets. It also speeds up the calculation by reducing the steps. 

Distributive property of multiplication over addition:

$a (b + c) = ab + ac$

Distributive property of multiplication over subtraction: 

$a(b\;-\;c) = ab\;-\;ac$

Example 1:  $2 \times (3 + 1)$

$2 \times (3 + 1) = 2 \times 4 = 8$ 

$2 \times (3 + 1) =(2 \times 3) + (2 \times 1) = 6 + 2 = 8$

In both cases, we get the same answer. Hence, the multiplication is distributive over addition.

Example 2:  $5 \times (4\;-\;2)$

$5 \times (4\;-\;2) = 5 \times 2 = 10$ 

$5 \times (4\;-\;2) = (5 \times 4)\;-\;(5 \times 2) = 20\;-\;10 = 10$

The multiplication is distributive over subtraction.

Identity Property of Multiplication

The identity property of multiplication states that if you multiply any number by 1, the answer will be the number itself. It is represented as $a \times 1 = a$.

Examples:

$3 \times 1 = 3$

$7 \times 1 = 7$

Zero Property of Multiplication

According to the zero property of multiplication, when a number is multiplied with 0, the product is always 0. 

It is represented as, $a \times 0 = 0$.

Examples:  

$42 \times 0 = 0$

$0 \times 23 = 0$.

Other Important Properties of Multiplication

Let’s discuss a few other important properties of multiplication.

Closure Property of Multiplication

The closure property of multiplication states that when a set of numbers is closed under multiplication, then the product of any two numbers from the set belongs to the set itself. 

Example 1: The multiplication of two integers is also an integer. If a and b are integers, then $c = a \times b$ will also be an integer. So, integers are closed under multiplication. For example, $(\;-\;2) \times 8 = (\;-\;16)$.

Example 2: The product of any two rational numbers is also a rational number.

Multiplication Property of Equality

If we multiply both sides of an equation with the same number, the equality holds. 

If $a = b$, then $a \times c = b \times c$

Consider an equation $\frac{1}{2}x = 50$

Multiply both sides by 2, we get

$\frac{1}{2}x \times 2 = 50 \times 2$

$x = 100$

Inverse Property of Multiplication

The multiplicative inverse property states that if we multiply a number with its reciprocal (multiplicative inverse), the product is always equal to 1.

The reciprocal is defined as the multiplicative inverse of a number and the reciprocal of a number is given by 1 divided by that number.

It represented by $a \times 1a = 1$. 

Rules of Multiplying Signed Numbers

Operation	Sign
$(+) \times (+)$ Positive $\times$ Positive	$(+)$ Positive
$(\;-\;) \times (\;-\;)$ Negative $\times$ Negative	$(+)$ Positive
$(+) \times (\;-\;)$ Positive × Negative	$(-)$ Negative
$(\;-\;) \times (+)$ Negative $\times$ Positive	$(-)$ Negative

Facts about Properties of Multiplication

Conclusion

In this article, we learned about the properties of multiplication: associative property, commutative property of multiplication, distributive property of multiplication, identity property of multiplication, zero property of multiplication. Let’s solve a few examples and practice problems now to understand the concept better.

Solved Examples on Properties of Multiplication

1. Identify the properties of multiplication used in each equation.

(i)   $7 \times 5 = 5 \times 7 = 12$

(ii)  $4 \times (3 \times 8) = (4 \times 3) \times 8$

(iii) $1 \times 46 = 46$

(iv) $34 \times \frac{1}{34} = 1$

Solution: 

(i)   $7 \times 5 = 5 \times 7 = 12$

Commutative property of multiplication

(ii)  $4 \times (3 \times 8) = (4 \times 3) \times 8$

Associative property of multiplication

(iii) $1 \times 46 = 46$

Identity property of multiplication

(iv) $34 \times \frac{1}{34} = 1$

Inverse property of multiplication.

2. Find the missing numbers. 

$12 \times (4 + 3)= \underline{} + \underline{}$

Solution: 

The distributive property of multiplication over addition is given by

 $a(b + c) = ab + ac$

Thus, we can write

$(4 + 3) \times 12 = (4 \times 12) +(3 \times 12)$

$(4 + 3) \times 12 = 48 + 36$

3. Fill in the blanks: $17 \times (90 \times 11) = (17 \times \underline{}) \times 11$

Solution: 

By the associative property of multiplication, we have

$a \times (b \times c) = (a \times b) \times c$

Thus, 

$17 \times (90 \times 11) = (17 \times 90) \times 11$

4. Find the product of $75 \times \;-\;31 \times \frac{1}{75}$ using suitable properties.

Solution: 

$75 \times (\;-\;31) \times \frac{1}{75} = (75 \times \frac{1}{75}) \times (\;-\;31)$ ..Commutative and associative property 

$= 1 \times(\;-\;31)$ ..Inverse property

 $=\;-\;31$  ..Identity property

Practice Problems on Properties of Multiplication

Frequently Asked Questions on Properties of Multiplication