What Does Vertical Mean in Geometry?
A vertical line is the one that we draw from top to bottom. In mathematics, vertical and horizontal alignment are represented by vertical and horizontal lines.
On the coordinate plane, the y-axis is referred to as the vertical axis, and all the vertical lines are parallel to this axis.
Recommended Games
What Is a Vertical Line in Math?
A vertical line is a line perpendicular to a horizontal line or the x-axis. In a coordinate plane, the y-axis is a vertical line since it is perpendicular to the x-axis, the baseline. Thus, any line that is parallel to the y-axis is vertical. A vertical line is also called a standing line.
Examples of vertical lines:
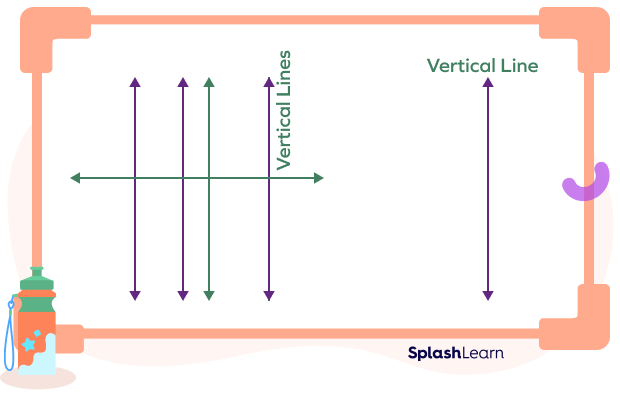
Recommended Worksheets
Vertical Line Definition
A vertical line is a straight line that runs from the top to the bottom, parallel to the y-axis, on the coordinate plane. It has an undefined slope and an equation of the form x = c, where “c” represents a constant value, indicating that the x-coordinate remains constant for all points on the line.
Properties of Vertical Lines
- Vertical lines are parallel to the y-axis. Thus, they do not intersect the y-axis. In other words, they do not have a y-intercept.
- The equation of a vertical line is of the form of x = a, where a is the x-intercept.
- Since the x-coordinates of a vertical line do not change (x is constant), the denominator of the slope (run) is always zero. Thus, the slope of a vertical line is undefined.
- A vertical line intersects a horizontal line at a right angle.
Equation of a Vertical Line
The equation of a vertical line in math can be given by x = ± a, where (a,0) is the x-intercept, the point where the line intersects the x-axis,
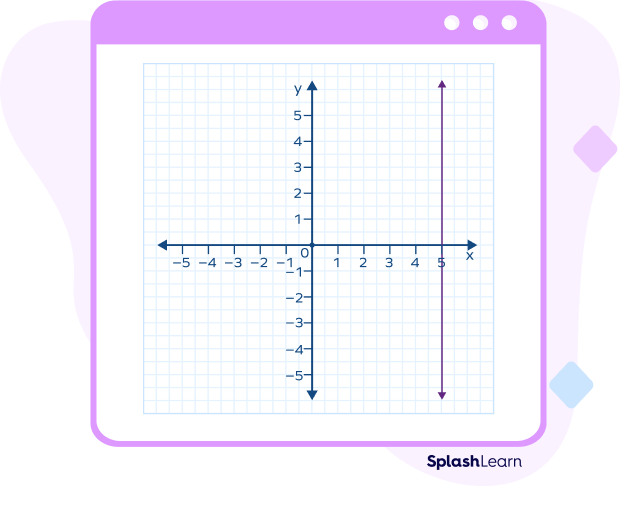
For example, consider the line which intersects the x-axis at (5,0) and is parallel to the y-axis. We get the equation of the line as x = 5.
Vertical and Horizontal Alignment
In geometry and its applications, one of the skills we prefer our kids to learn by instinct or cultivate within themselves is the line of sight. Line of Sight refers to our ability to observe and look at things from our point of view. Depending on the context, we change our perspective to view things in different alignments or rotations. The most elementary perspectives or alignments in which we view objects are horizontal and vertical.
- Vertical Alignment: Vertical alignment is when we view things from top to bottom. It is referred to as the alignment when things are standing.

- Horizontal Alignment: Horizontal alignment is when we view things from left to right. It is referred to as the alignment when things are in the sleeping position.
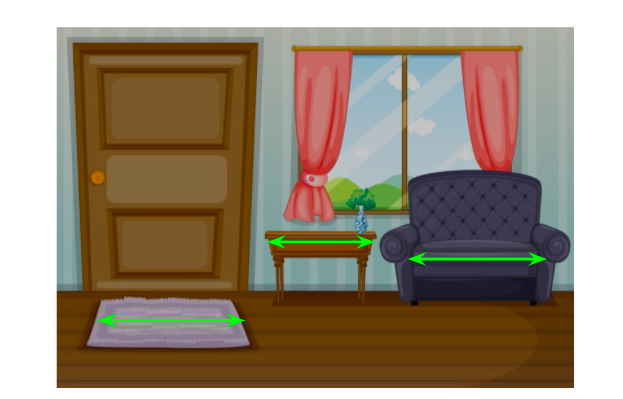
- Vertical Movements: In our day-to-day life, we notice various things in vertical alignment, like a standing building or a powerhouse, etc. The word vertical can also be used to describe the motion of objects. Since we know vertical stands for top to bottom, the motion of an apple falling from a tree is vertical.
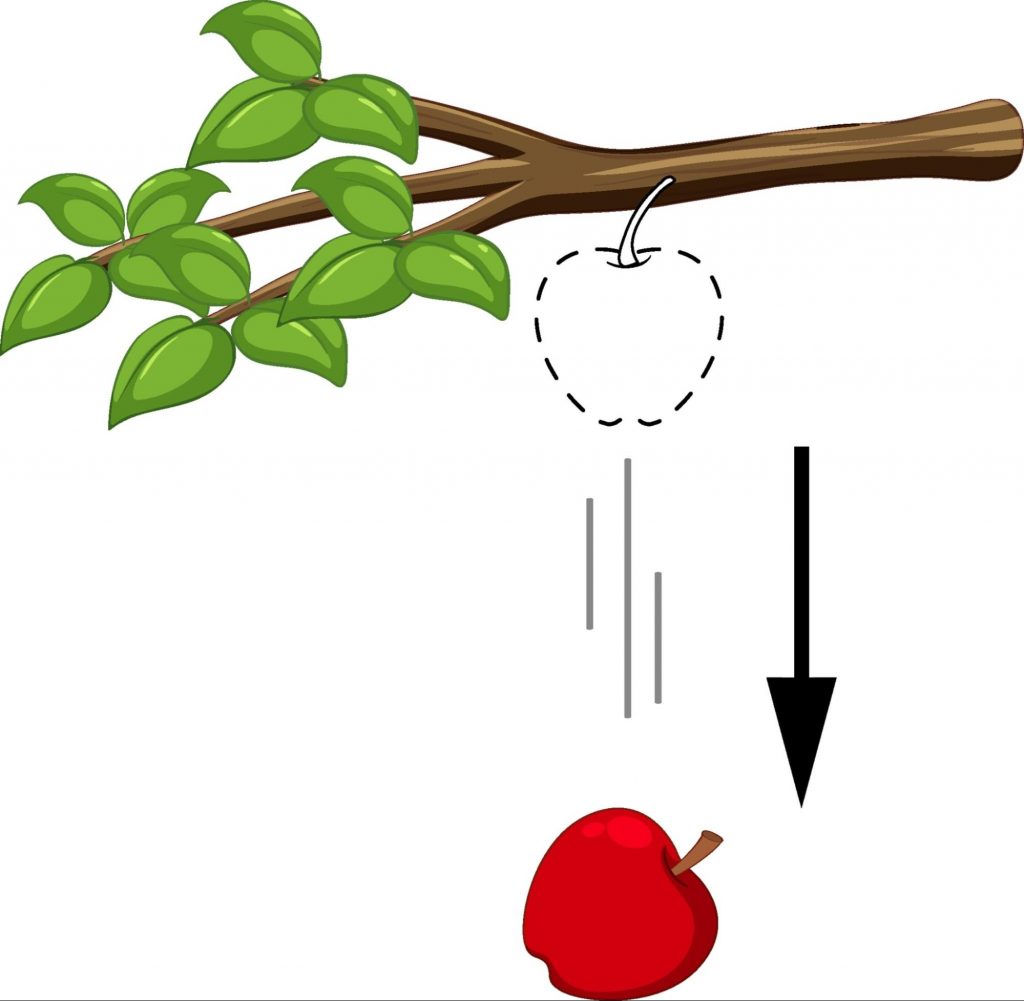
The motion of a rocket going from bottom to top is also classified as vertical.

Vertical Line on the Coordinate Plane
- On a coordinate plane, the x-axis is considered the horizontal axis, whereas the y-axis is the vertical axis.
- The graph of a vertical line in a coordinate plane is a line parallel to the y-axis.
- For a vertical line, all the points on the line have the same x-coordinate. Thus, the x-coordinate stays the same; only the y-coordinate changes. A vertical line never intersects the y-axis.
Example 1: The line x = 5 is a vertical line. It is parallel to the y-axis.
Example 2: In the given image, the line PQ is parallel to the y-axis, making it a vertical line.
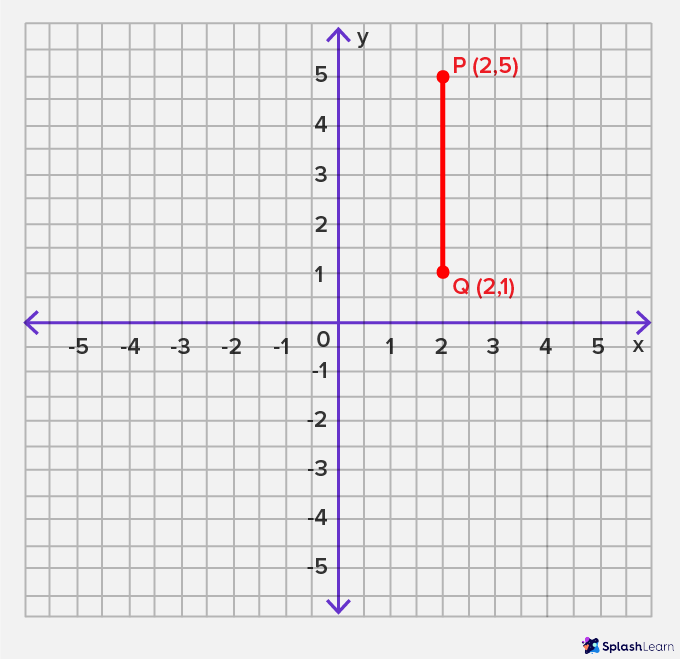
How to Draw a Vertical Line
Let’s learn how to draw a vertical line.
- Using a Ruler: To draw a vertical line using a ruler, keep the ruler in a standing position, perpendicular to the edge of the page, and draw the line from bottom to top or top to bottom.

- Drawing a vertical line on a coordinate grid: To draw a vertical line on a coordinate plane, follow these steps:
Step 1: Plot any point on the coordinate plane. For example, let’s plot (4,3).
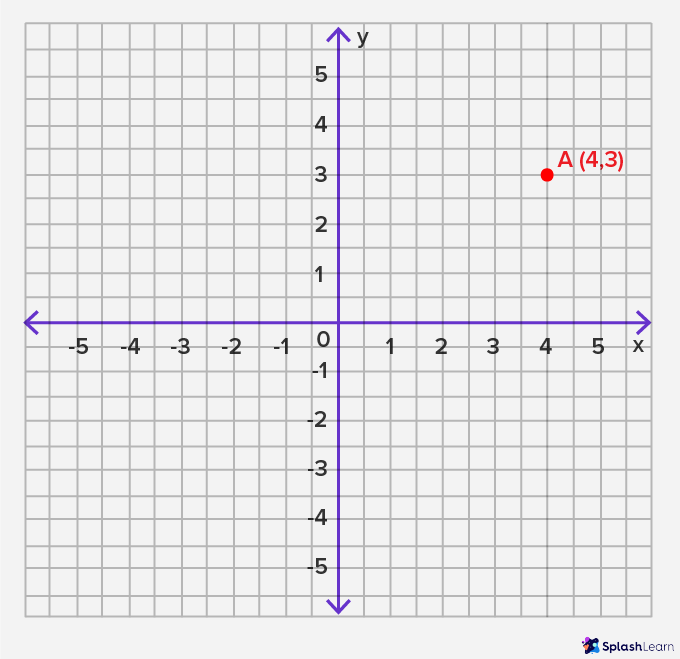
- Step 2: Identify the x-coordinate of the point marked. Here, it is 4.
- Step 3: Plot another point on the coordinate plane with the same x-coordinate. For example, let’s plot (4, -2).
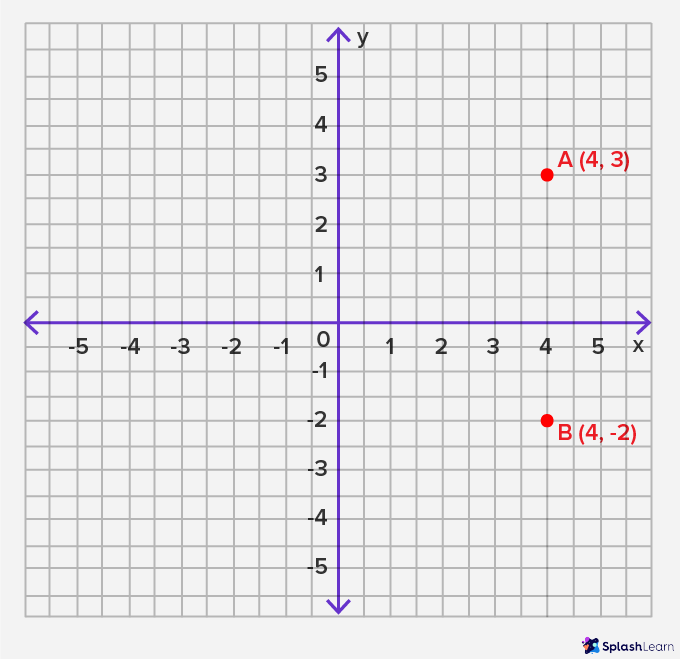
Step 4: Join the two plotted points using a ruler to get a vertical line.
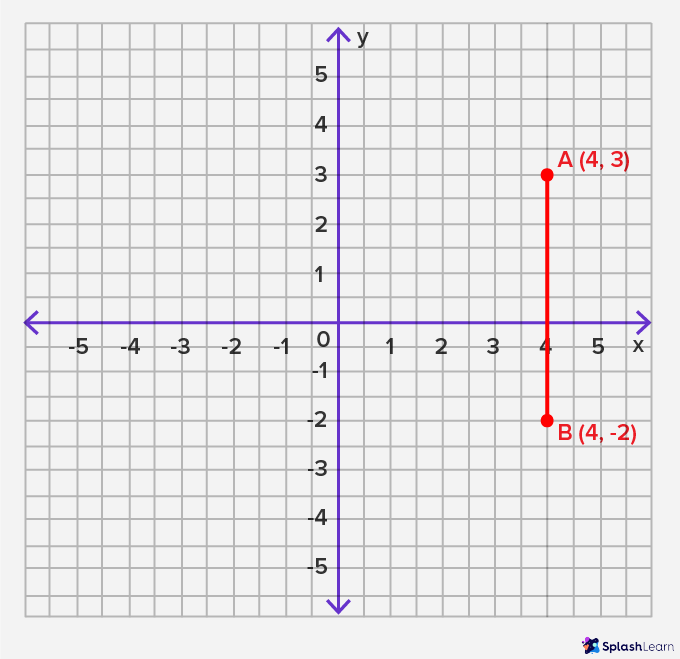
Uses of Vertical Lines
Vertical lines have great applications in various fields, such as symmetry and photography.
A vertical line of symmetry runs across the image from top to bottom or bottom to top and divides the image into identical halves.
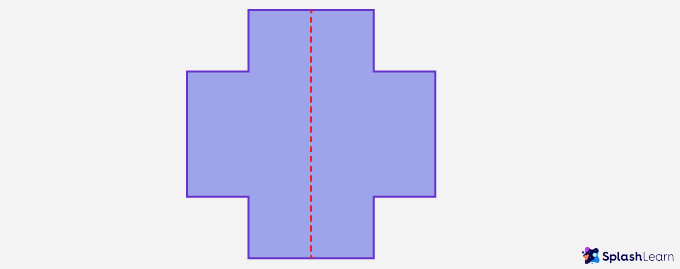
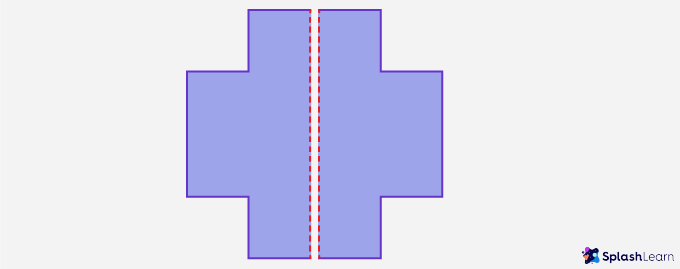
Cameras are designed to photograph in landscape (horizontal) or portrait (vertical) mode. In horizontal mode, photographs are wider than they are tall. In vertical mode, photographs are taller than they are wide.
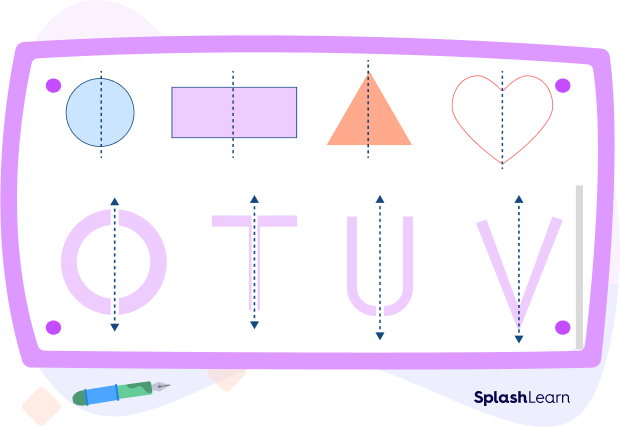
Vertical Lines of Symmetry
When a vertical line goes through the middle of a shape from top to bottom, dividing it into two identical halves, it is called a vertical line of symmetry.
Slope of a Vertical Line
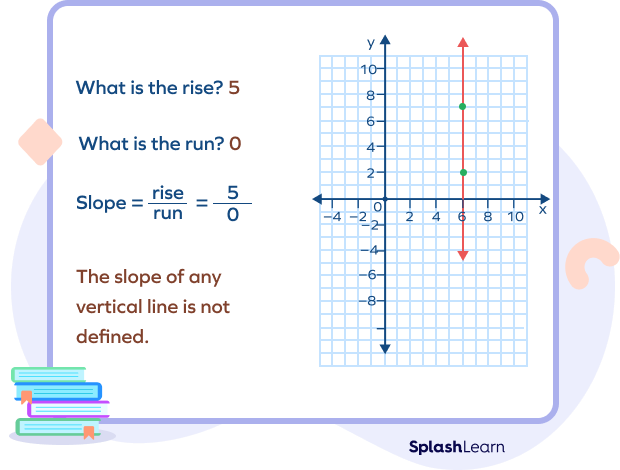
The slope of a line tells us how steep a line is. If a line passes through two points having coordinates (x1,y1) and (x2,y2), then we can define the slope of a line as
Slope = m = y2- y1x2- x1 = yx = Change in yChange in x = RiseRun
As mentioned earlier, the x-coordinate remains constant in the equation of a vertical line, and only the y-coordinate changes. Thus, the denominator in the slope formula becomes 0. Since the division by 0 is not defined, the slope of a vertical line is undefined.
Difference between Horizontal Line and Vertical Line
| Horizontal Line | Vertical Line |
|---|---|
| It is parallel to the x-axis. | It is parallel to the y-axis. |
| It is perpendicular to the y-axis. | It is perpendicular to the x-axis. |
| The equation is of the form y = ± a, where a is any real number. | The equation is of the form x = ± b, where b is any real number. |
| The slope of a horizontal line is 0. | The slope of a vertical line is undefined. |
 |  |
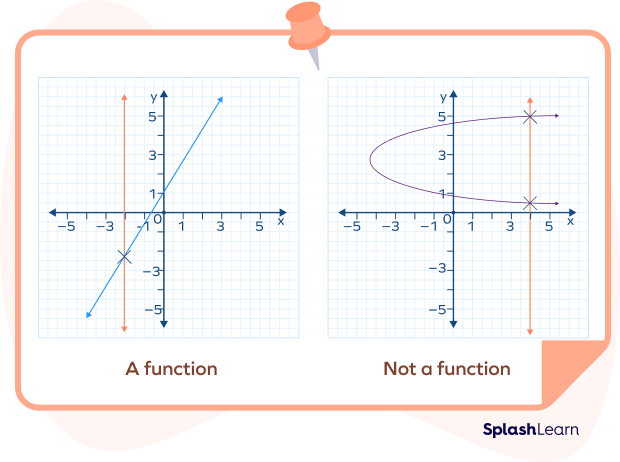
Vertical Line Test
A vertical line test assesses whether a given graph represents a function. It is based on the fact that a function can only have one output for every input. This test ensures that for each input (x-value), there is only one corresponding output (y-value), satisfying the criteria of a function.
If, in a graph, a vertical line has more than one intersection, it means that there is more than one output for a single input, which means it cannot be a function.
Thus, any vertical line in the plane can only ever cross the graph of a function once.
Vertical line test examples:
Facts about Vertical Lines
- The slope of a vertical is always undefined.
- A vertical line always goes from top to bottom, making a 90-degree angle with the x-axis.
Conclusion
In this article, we learned about vertical lines, their meaning, uses, construction, properties, equation, and slope. Let’s look at a few examples and practice problems for better comprehension.
Solved Examples on Vertical Lines
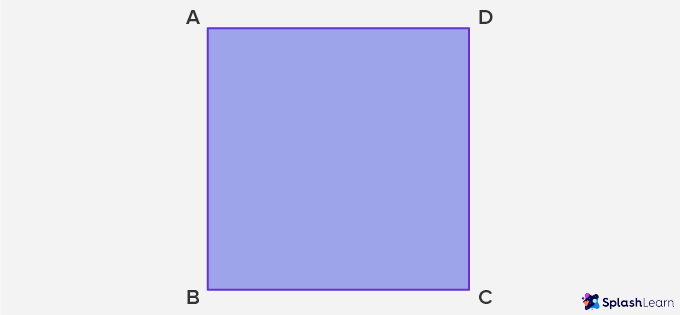
1. In the square ABCD, which sides (line segments) represent vertical lines?
Solution:
Lines AB and CD are vertical lines.
Example 2: Does the given letter have a vertical line of symmetry or not?

Solution:
Yes.
You can draw a vertical line dividing the letter into two identical halves.

Example 3: Can you find any number between 0 to 9 with a vertical line of symmetry?
Solution:
Numbers 0 and 8 have vertical symmetry.
You can divide them into two halves by drawing a vertical line of symmetry.
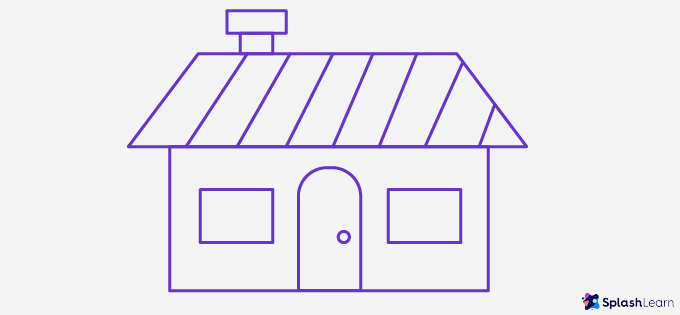
Example 4: How many vertical lines are there in a given figure?
Solution:
There are 10 vertical lines in the given figure.
5. Find the slope of the line x=-3.
Solution:
Since x=-3 is a line parallel to the y-axis, it is a vertical line.
The slope of this line is undefined.
6. Find the equation of the vertical line passing through the point (2, –4).
Solution:
The equation of the vertical line is of the form x = ± a, where a is the x-intercept.
Since the line passes through (2, –4), the x-intercept is 2.
Thus, the equation of the vertical line is x = 2.
We can also write it as x – 2 = 0.
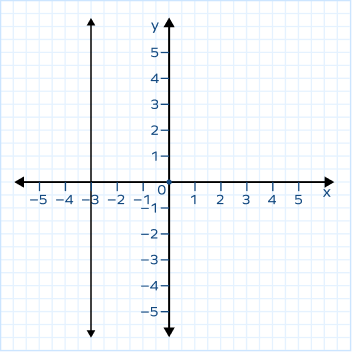
7. Find the equation of the line given in the figure.
Solution:
The line is parallel to the y-axis and passes through the point (–3, 0) on the x-axis.
Thus, the x-intercept is –3.
The equation of the given vertical line is x = –3.
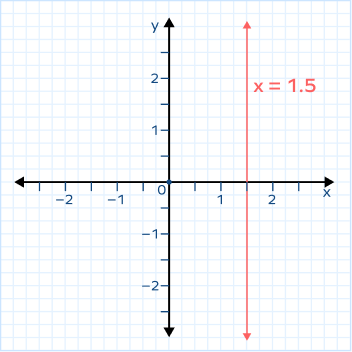
8. Plot the line x = 1.5 on a graph.
Solution:
x = 1.5 represents a vertical line passing through the point (1.5, 0).
Practice Problems on Vertical Lines
Vertical
The slope of the line $x = 10$ is
Since $x = 10$ gives us a line parallel to the y-axis, the slope of this line cannot be defined.
A vertical line is parallel to the _____.
A vertical line is parallel to the y-axis.
Which of the following equations represents a vertical line?
The equation $x = 2.5$ represents the vertical line.
Which of the following objects are not vertically placed?
A mattress is placed in a lying position, not a vertical position.
Which of the following letters has a vertical line of symmetry?
Letter H has a vertical line of symmetry.
Which of the following has vertical movement?
The elevator in the building has top-to-bottom or bottom-to-up movement. Moving trains and conveyor belts move horizontally, and escalators move on an inclined plane.
All vertical lines are parallel to _______________.
On the coordinate plane, the y-axis is referred to as the vertical axis, and all the vertical lines are parallel to this axis.
Frequently Asked Questions about Vertical Lines
What are horizontal lines?
Lines parallel to the x-axis, making a right angle with the y-axis are called horizontal lines.
What is the slope of a horizontal line?
The slope of a horizontal line is 0.
Which direction is considered vertical?
The up and down direction is the vertical direction.
How can we identify a vertical line?
A vertical line is drawn in the up and down direction, from top to bottom, on a page or a shape. It intersects a horizontal line at a right angle.
Which axis are vertical lines perpendicular to in the coordinate plane?
A vertical line is perpendicular to the x-axis in the coordinate plane.
What does it mean when something is vertical?
It means that the object is in a standing position.




































