Twin Primes – Definition, List, Properties, Examples, Facts, FAQs

What Are Twin Primes in Math?

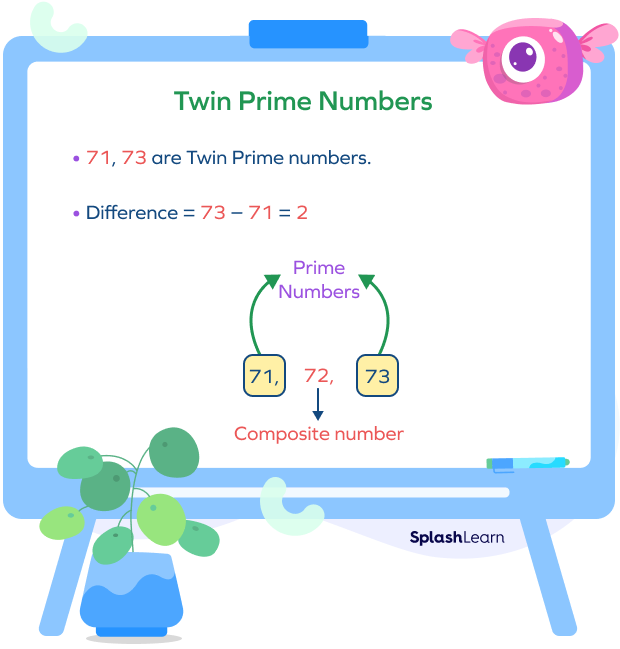
Twin primes are two prime numbers that have a difference of 2 between them. Twin primes are also known as prime pairs or prime twins.

Twin primes examples: $\left\{3, 5\right\},\; \left\{5, 7\right\},\; \left\{11, 13\right\}$, etc 

What do you notice? 

$5 \;-\; 3 = 2$

$7 \;-\; 5 = 2$

$13 \;-\; 11 = 2$

In other words, there is only one composite number between two prime twins. 

We know that a prime number is a natural number greater than 1 that has only two factors, 1 and the number itself. 

Examples: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, …

Composite numbers are numbers that have more than two factors (but a finite number of factors).

Twin Primes: Definition

Two prime numbers are said to be twin primes if the difference between them is 2. 

For example, $(p,\; p + 2)$ is said to be a twin prime pair if both p and $(p + 2)$ are prime numbers.

How to Know if Two Numbers Are Twin Primes

Step 1: Check if the given numbers are prime numbers. If either of them is not a prime number, the two numbers are not twin primes.

Step 2: If the two numbers are prime, find the difference between them.

Step 3: If the difference between two prime numbers is 2, the two prime numbers are twin primes.

Example: Do 2 and 5 make a twin prime pair?

2 and 5 are prime numbers.

The difference between 2 and $5 = 5 \;-\; 2 = 3$

The difference between 2 and 5 is not 2. 

Thus, (2, 5) is not a twin prime pair.

Properties of Twin Prime Numbers

• There are an infinite number of twin primes.
• The difference between twin prime numbers is always 2. 
• The prime number 5 is the only prime number present in two twin prime pairs, which are $\left\{3, 5\right\}$ and $\left\{5, 7\right\}$.
• Every twin prime pair is of the form of $(6n \;-\; 1,\; 6n + 1)$, where n is any natural number. The only exception to this is $\left\{3,\; 5\right\}$.
• The sum of every twin prime pair is divisible by 12. The only exception for this property is the twin-prime pair $\left\{3,\; 5\right\}$. 

First Pair of Twin Prime Numbers

The first pair of twin prime numbers is $\left\{3,\; 5\right\}$. 

The smallest prime number is 2 and the list of prime numbers is given by

2, 3, 5, 7, 11, 13, 17, 19, …

Note that (2, 3) is not a twin prime pair since there is no composite number between them.

$3\;-\;2 = 1$

However, we have $5\;-\;3 = 2$

Thus, the first pair of prime numbers to satisfy the main condition of twin prime numbers is (3, 5). The difference between 3 and 5 is two. 

List of Twin Primes

First 15 pairs of Twin Primes	$\left\{3, 5\right\},\; \left\{5, 7\right\},\; \left\{11, 13\right\},\; \left\{17, 19\right\},\; \left\{29, 31\right\},\; \left\{41, 43\right\},\; \left\{59, 61\right\},\; \left\{71, 73\right\},\; \left\{101, 103\right\},\; \left\{107, 109\right\},\; \left\{137, 139\right\},\; \left\{149, 151\right\},\; \left\{179, 181\right\},\; \left\{191, 193\right\},\; \left\{197, 199\right\}$
Twin Prime Pairs from 1 to 50	$\left\{3, 5\right\},\; \left\{5, 7\right\},\; \left\{11, 13\right\},\; \left\{17, 19\right\},\; \left\{29, 31\right\},\; \left\{41, 43\right\}$
Twin Prime Pairs from 50 to 100	$\left\{59, 61\right\},\; \left\{71, 73\right\}$
Twin Prime Pairs from 100 to 200	$\left\{101, 103\right\},\; \left\{107, 109\right\},\; \left\{137, 139\right\},\; \left\{149, 151\right\},\; \left\{179, 181\right\},\; \left\{191, 193\right\},\; \left\{197, 199\right\}$
Twin Prime Numbers from 201 to 300	$\left\{227, 229\right\},\; \left\{239, 241\right\},\; \left\{269, 271\right\},\; \left\{281, 283\right\}$
Twin Prime Numbers from 301 to 400	$\left\{311, 313\right\},\; \left\{347, 349\right\}$
Twin Prime Numbers from 401 to 500	$\left\{419, 421\right\},\; \left\{431, 433\right\},\; \left\{461, 463\right\}$
Twin Prime Numbers from 501 to 1000	$\left\{521, 523\right\},\; \left\{569, 571\right\},\; \left\{599, 601\right\},\; \left\{617, 619\right\},\; \left\{641, 643\right\},\; \left\{659, 661\right\},\; \left\{809, 811\right\},\; \left\{821, 823\right\},\; \left\{827, 829\right\},\; \left\{857, 859\right\},\; \left\{881, 883\right\}$

Twin Primes Conjecture

Conjecture is an opinion or statement without proof. 

The Twin Prime Conjecture states that there are infinite pairs of prime numbers. In other words, the twin prime conjecture states that there are infinitely many prime numbers p such that (p + 2) is also a prime number. 

It is also known as Polignac’s conjecture, as the French mathematician Alphonse de Polignac was the first to introduce this idea in 1849. 

Various Other Prime Types

Some different types of prime numbers are as follows:

Cousin Primes

The prime numbers that differ by four are called cousin primes. 

For example: (3, 7) and (7, 11)

Prime Triplets

A prime triplet is a set of three prime numbers that can be represented in the following form: $(p, p + 2, p + 6)$ or $(p, p + 4, p + 6)$, where p is a prime number.

For example: (5, 7, 11) and (7, 11, 13)

Co-prime Numbers

Two numbers that have just 1 as a common factor are co-prime are called co-prime numbers or relatively prime numbers.

For example: (13 and 14)

Twin Prime Numbers and Co-prime Numbers

Twin Prime Numbers	Co-prime Numbers
The prime numbers whose difference is two.	Co-prime numbers are the two numbers that have only 1 as a common factor.
Twin prime numbers must be prime numbers.	Co-prime numbers need not be prime numbers. Two composite numbers can also be co-prime.
All twin primes are co-primes.	All co-primes are not twin prime numbers. For example: (13 and 14) are co-primes but not twin primes.
(3 and 5), (5 and 7), and (11 and 13) are some examples of twin prime numbers.	(2 and 3), (4 and 5), and (3 and 7) are some examples of co-prime numbers.

Facts about Twin Prime Numbers

Conclusion

In this article, we learned about twin primes, their properties, and the list of twin primes. Let’s solve a few examples and practice problems.

Solved Examples of Twin Primes

1. How many twin prime pairs can be found between 1 and 50?

Solution:

The 6 pairs of twin prime numbers between 1 and 50 are as follows:

• (3, 5)
• (5, 7)
• (11, 13)
• (17, 19)
• (29, 31)
• (41, 43)

2. Write the first 5 pairs of twin prime numbers.

Solution:

Prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …

We will begin with the first two prime numbers, 2 and 3 and we will check if they satisfy the conditions of twin primes. As the difference between 2 and 3 is not equal to 2, they are not twin primes. So, we will move on to the next pair, (3, 5). 

As 3 and 5 satisfy the conditions, we can call them twin primes. Repeating the above steps, we will get the first five pairs of twin prime numbers:

(3, 5), (5, 7), (11, 13), (17, 19), and (29, 31).

3. Is (13, 15) a pair of twin primes?

Solution:

Difference $= 15\;-\;13 = 2$

The difference between the given two numbers is 2.

13 is a prime number. However, 15 is not a prime number.

Thus, (13, 15) is not a twin prime pair.

Practice Problems on Twin Primes

Frequently Asked Questions on Twin Primes