What Is an Addition Table?
An addition table is a chart created using a particular pattern by arranging the numbers in rows and columns, which helps to learn how to add numbers together.
Addition in math is a process of combining two or more numbers. We can quickly calculate the sum of two numbers using the addition table without actually adding them. It helps to develop a number sense, or fluency with operations. Hence, an addition table comes handy. Fluency with the addition table provides a milestone for understanding calculations related to additions.
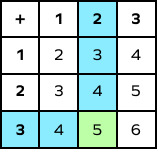
Here’s an example of an addition table for 1 to 5 to understand this better. There are 5 rows and 5 columns. The first row and the first column represents the numbers to be added (addends). The box or cell where a row and a column intersect represents the sum of two corresponding numbers.
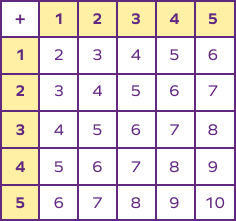
Addition table is a tabular representation of numbers arranged in rows and columns that allows us to calculate the sum of two numbers simply by looking at the chart rather than doing the math.
Recommended Games
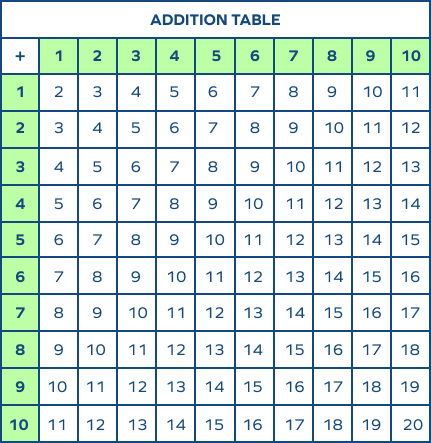
Addition Table 1 to 10
Here’s the addition table chart for 1 to 10.
Recommended Worksheets
How to Use an Addition Table
The first row and the first column represent 1–10 numbers. These are the numbers to be added.
To add two numbers using the addition table, we follow these simple steps.
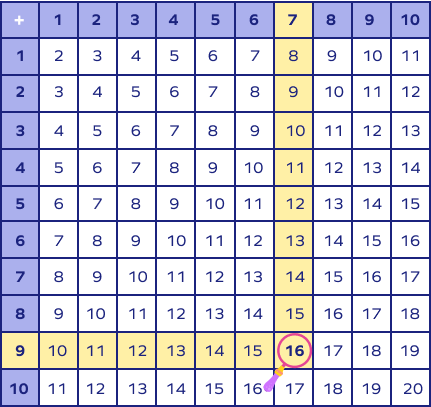
Let’s find $9 + 7$.
Step 1: Choose the first number from the first column (or the top row).
Step 2: Choose the second number from the top row.
Step 3: Find the intersection of the row and column. The value in the box is 14.
Therefore, $9 + 9 = 14$.
Steps 1 and 2 can also be reversed. It means that the order of choosing numbers from the row and column can be reversed. It doesn’t matter in which sequence we choose the numbers. It is because the addition operation is commutative.
Addition Facts Table
An addition fact is defined as the sum of two one-digit addends. Example: $1 + 2 = 3$ is an addition fact.
| For 1 | For 2 | For 3 | For 4 | For 5 | For 6 | For 7 | For 8 | For 9 | For 10 |
| $1 + 1 = 2$ | $1 + 2 = 3$ | $1 + 3 = 4$ | $1 + 4 = 5$ | $1 + 5 = 6$ | $1 + 6 = 7$ | $1 + 7 = 8$ | $1 + 8 = 9$ | $1 + 9 = 10$ | $1 + 10 = 11$ |
| $2 + 1 = 3$ | $2 + 2 = 4$ | $2 + 3 = 5$ | $2 + 4 = 6$ | $2 + 5 = 7$ | $2 + 6 = 8$ | $2 + 7 = 9$ | $2 + 8 = 10$ | $2 + 9 = 11$ | $2 + 10 = 12$ |
| $3 + 1 = 4$ | $3 + 2 = 5$ | $3 + 3 = 6$ | $3 + 4 = 7$ | $3 + 5 = 8$ | $3 + 6 = 9$ | $3 + 7 = 10$ | $3 + 8 = 11$ | $3 + 9 = 12$ | $3 + 10 = 13$ |
| $4 + 1 = 5$ | $4 + 2 = 6$ | $4 + 3 = 7$ | $4 + 4 = 8$ | $4 + 5 = 9$ | $4 + 6 = 10$ | $4 + 7 = 11$ | $4 + 8 = 12$ | $4 + 9 = 13$ | $4 + 10 = 14$ |
| $5 + 1 = 6$ | $5 + 2 = 7$ | $5 + 3 = 8$ | $5 + 4 = 9$ | $5 + 5 = 10$ | $5 + 6 = 11$ | $5 + 7 = 12$ | $5 + 8 = 13$ | $5 + 9 = 14$ | $5 + 10 = 15$ |
| $6 + 1 = 7$ | $6 + 2 = 8$ | $6 + 3 = 9$ | $6 + 4 = 10$ | $6 + 5 = 11$ | $6 + 6 = 12$ | $6 + 7 = 13$ | $6 + 8 = 14$ | $6 + 9 = 15$ | $6 + 10 = 16$ |
| $7 + 1 = 8$ | $7 + 2 = 9$ | $7 + 3 = 10$ | $7 + 4 = 11$ | $7 + 5 = 12$ | $7 + 6 = 13$ | $7 + 7 = 14$ | $7 + 8 = 15$ | $7 + 9 = 16$ | $7 + 10 = 17$ |
| $8 + 1 =9$ | $8 + 2 = 10$ | $8 + 3 = 11$ | $8 + 4 =12$ | $8 + 5 =13$ | $8 + 6 =14$ | $8 + 7 =15$ | $8 + 8 =16$ | $8 + 9 =17$ | $8 + 10 = 18$ |
| $9 + 1 =10$ | $9 + 2 = 11$ | $9 + 3 = 12$ | $9 + 4 =13$ | $9 + 5 =14$ | $9 + 6 =15$ | $9 + 7 =16$ | $9 + 8 =17$ | $9 + 9 =18$ | $9 + 10 = 19$ |
| $10 +1 = 11$ | $10 + 2 = 12$ | $10 + 3 = 13$ | $10 + 4 = 14$ | $10 + 5 = 15$ | $10 + 6 = 16$ | $10 + 7 = 17$ | $10 + 8 = 18$ | $10 + 9 = 19$ | $10 + 10 = 20$ |
Patterns in Addition Table
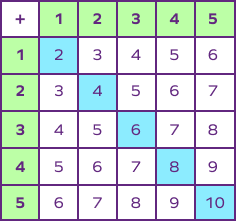
- The sum of two even numbers is an even number.
- 1 added to an even number that gives an odd number. This creates a checkerboard pattern or an alternate pattern in the addition table.
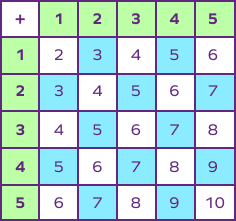
- The order of addends does not alter the result.
- 1 added to a number gives the successor of the number as the sum.
- The diagonal, from top left to bottom right, contains even numbers 2, 4, 6, 8, and 10 since these positions are filled by adding a number to itself. It is a number of the form 2n.
Facts about the Addition Table
- An addition fact is defined as the sum of two one-digit addends. Example: $1 + 2 = 3$ is an addition fact.
- The addition table helps with the addition of numbers by creating a pattern and arranging the numbers in rows and columns.
- When zero is added to any number, the number is unchanged.
For example, $5 + 0 = 5 = 0 + 5$. - Add numbers in any order, we get the same sum.
$5 + 6 + 7 = 18$
$6 + 7 + 5 = 18$
$7 + 5 + 6 = 18$ - The number or values being added are called addends and the answer is called the sum.
- If we add two even numbers, the outcome is also an even number, for example $4 + 4 = 8, 6 + 8 = 14$.
Conclusion
In this article, we have learned about addition table and how to use it. The chart for addition is a great tool for visually representing the way numbers add to form a sum. Now let’s solve some examples for better understanding.
Solved Examples on Addition Table
1. Write all the addition facts for the number 4 using the addition table.
Solution:
$1 + 4 = 5$
$2 + 4 = 6$
$3 + 4 = 7$
$4 + 4 = 8$
5 + 4 = 9
$6 + 4 = 10$
$7 + 4 = 11$
$8 + 4 = 12$
$9 + 4 = 13$
$10 + 4 = 14$
2. How will you find the value of $5 + 3$ using the addition table?
Solution:
Identify 5 in the top row. Identify 3 in the first column. Find the cell where they intersect each other.
Thus, $5 + 3 = 8$
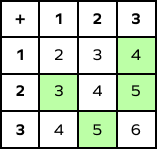
3. Complete the addition table.

Solution:
$3 + 1 = 4$
$1 + 2 = 3$
$3 + 2 = 5$
$2 + 3 = 5$
4. Amy has 2 apples and 3 oranges. What is the total number of fruits Amy has? Use addition table.
Solution:
Amy has 2 lemon sweets and 3 orange sweets.
To find the sum of 2 and 3, we need to locate where the row for number 2 meets the column for number 3.
Using the addition chart, we find that the total number of sweets Amy has is 5.
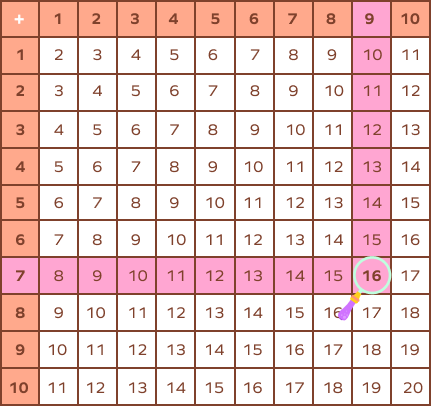
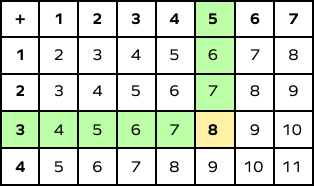
5. In the addition table, is the addition along diagonals in any given box the same? If yes, why?
Solution:
Take a look at the three highlighted boxes. Add along the diagonal in any box.
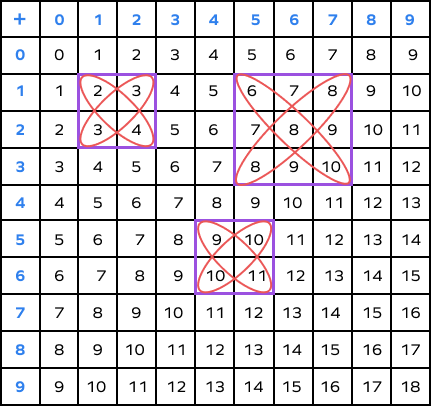
- $2 + 4 = 6$
$3 + 3 = 6$ - $6 + 8 + 10 = 24$
$8 + 8 + 8 = 24$ - $9 + 11 = 20$
$10 + 10 = 20$
The sums along diagonals are always equal. Due to the position of numbers in the addition table, the sum always gets compensated. If 1 is added to one of the addends, it gets subtracted from the other, leaving the addition unaltered.
Practice Problems on Addition Table
Addition Table: Addition Table 1 to 10, Tips, Examples, Facts, FAQs
In addition table, the result of $4 + 5$ and the result of $5 + 4$ is the same. What property of addition does this show?
Commutative property of addition states that changing the order of addends does not change the sum. For example, $4 + 5 = 5 + 4$
The addends in the equation $2 + 11 = 13$ are ________.
The number or values being added are called addends. Thus, here 2 and 11 are addends.
In the addition table, the first row and the first column represent ________.
The first row (row at the top) and the first column represent the addends (numbers to be added.)
The addition of two even numbers is ________.
If we add two even numbers, the outcome is also an even number, for example $4 + 4 = 8, 6 + 8 = 14$.
The numbers along the diagonal of the addition table are
The numbers along the diagonal of the addition table are even numbers.
Frequently Asked Questions about the Addition Table
What are the properties of addition?
The four main properties of addition are commutative, associative, distributive, and additive identity.
What is the compensation method of addition?
“Compensation” is where you round up a number and then take away the extra after you have added. This makes adding easier.
For example: $29 +16$
$30 + 16 = 46$
Take away the extra $1.46 \;-\; 1 = 45$
What is the column method of addition?
The column method is a method of adding numbers by aligning the place values.
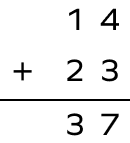
Can we add larger numbers using an addition table ?
The addition table can be expanded to include as many numbers as desired. So, we can use the addition tables to add large numbers as well.
Does the order of numbers matter in addition of real numbers?
No, the real numbers can be added in any order. Addition is commutative.




































