Algebraic Identities: Definition, Factorization, Proof, Examples, FAQs

What Are Algebraic Identities?

An algebraic identity is basically an equation in which L.H.S. equals R.H.S. for all values of the variables. An identity in math is an equation that holds true for all the values, even if you change the variables involved. For every value of the variables, an algebraic identity indicates that the left and right sides of the equation are identical.

Algebraic identities are equations that hold true for all values of variables.

In mathematical identities, the values on the left and right sides of the equation are exactly the same. We use algebraic identities as a set of formulas that help us in simplifying and solving algebraic equations. 

Consider an example.

To expand the algebraic expression $(x + 1)^2$, you will have to multiply $(x + 1)$ with itself. It will surely be lengthy and time consuming.
However, if you use the algebraic identity $(a + b)^2 = a^2 + 2ab + b^2$, you will simply have to substitute the values and your job is done!

Algebraic Identity Definition

An important set of mathematical formulas or equations where the value of the L.H.S. of the equation is equal to the value of the R.H.S. of the equation. 

Algebraic identities simplify algebraic expressions and calculations. 

Here are examples of common algebraic identities:

• $(a + b)^2 = a^2 + 2ab + b^2$
• $(a \;−\; b)^2 = a^2 \;−\; 2ab + b^2$
• $a^2 \;−\; b^2 = (a + b)(a \;−\; b)$
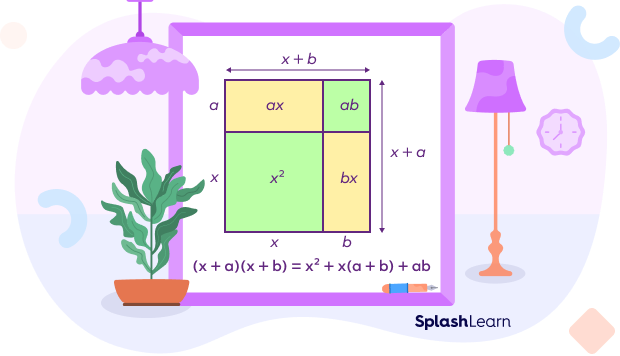
• $(x + a)(x + b) = x^2 + x(a + b) + ab$

Algebraic Identities with Two Variables

The algebraic identities with two variables are known as two variable identities. Some basic two-variable algebraic identities are as follows:

• $(a + b)^2 = a^2 + 2ab + b^2$
• $(a \;−\; b)^2 = a^2 \;−\; 2ab + b^2$
• $a^2 \;−\; b^2 = (a + b)(a \;−\; b)$
• $(a + b)^3 = a^3 + 3a^2 b + 3ab^2 + b^3$
• $(a \;− \;b)^3 = a^3 \;−\; 3a^2b + 3ab^2 \;−\; b^3$

Algebraic Identities with Three Variables 

Some of the most important algebraic identities that use three variables are as follows:

• $(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ac$
• $a^3 + b^3 + c^3 \;−\; 3abc = (a + b + c)(a^2 + b^2 + c^2 \;−\; ab \;−\; ca \;−\; bc)$

Two identities can be derived from the above two identities.

• $a^2 + b^2 + c^2 = (a + b + c)^2 \;−\; 2(ab + bc + ac)$
• $(a + b)(b + c)(c + a) = (a + b + c)(ab + ac + bc) − 2abc$

How to Prove Algebra Identities

Algebraic identities can be proved by verifying if the L.H.S. (left-hand side) is equal to R.H.S. (right-hand side). Here, you have to solve and simplify the expression on one side (or both sides) using simple arithmetic operations.

Proof of Algebra Identities

Let’s look at the proof of some fundamental algebraic identities.

Proof of (a + b)² = a² + 2ab + b²

This formula is used to find the square of a binomial involving addition.

L.H.S. $= (a + b)^2$

L.H.S. $= (a + b) \times (a + b)$

L.H.S. $= a^2 + ab + ba + b^2$

L.H.S. $= a^2 + 2ab + b^2$

L.H.S. $=$ R.H.S.

Hence proved.

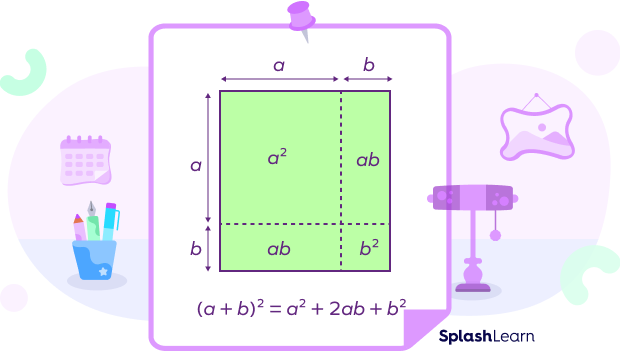
Proof of (a − b)² = a² − 2ab + b²

This identity helps to expand the square of the difference between the two variables.

L.H.S. $= (a \;−\; b)^2$

L.H.S. $= (a \;−\; b) \times (a \;−\; b)$

L.H.S. $= a^2 \;−\; ab \;−\; ba + b^2$

L.H.S. $= a^2 \;−\; 2ab + b^2$

L.H.S. $=$ R.H.S.

Hence proved.

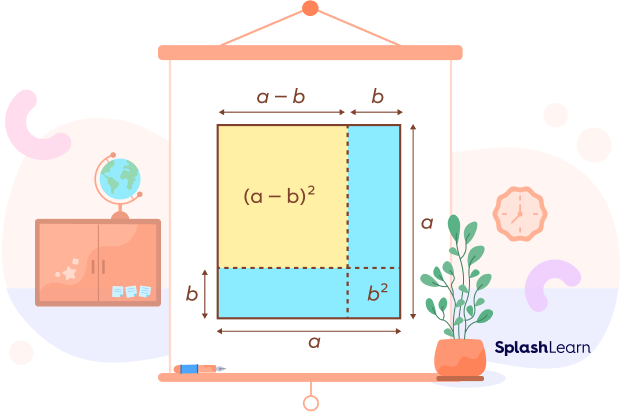
Proof of (a + b)(a – b) = a² – b²

This identity helps to find the difference between two squares without actually calculating the individual square numbers.

L.H.S. $= (a + b)(a \;−\; b)$

L.H.S. $= a^2 \;−\; ab + ba \;−\; b^2$

L.H.S. $= a^2 \;− \;b^2$

L.H.S. $=$ R.H.S.

Hence proved.

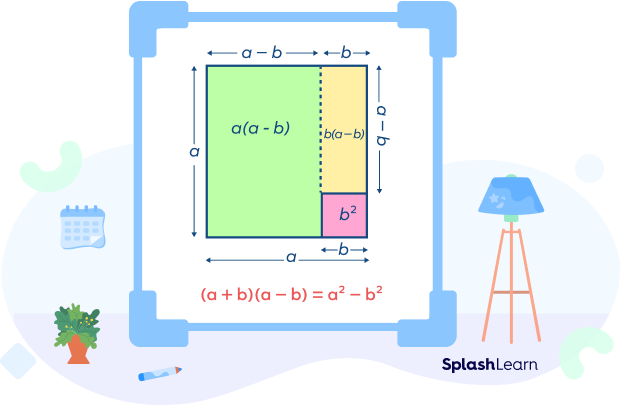
Proof of (x + a)(x + b) = x² + x(a + b) + ab

L.H.S. $= (x + a)(x + b)$

L.H.S. $= x^2 + bx + ax + ab$

L.H.S. $= x^2 + x(a + b) + ab$

L.H.S. $=$ R.H.S.

Hence proved.

List of Standard Algebraic Identities

Identity 1	$(a + b)^2 = a^2 + 2ab + b^2$
Identity 2	$(a \;–\; b)^2 = a^2 – 2ab + b^2$
Identity 3	$a^2 \;–\; b^2 = (a + b)(a \;–\; b)$
Identity 4	$(x + a)(x + b) = x^2 + (a + b)x + ab$
Identity 5	$(a + b)^3 = a^3 + b^3 + 3ab (a + b)$
Identity 6	$(a \;–\; b)^3 = a^3 \;–\; b^3 \;–\; 3ab (a \;–\; b)$
Identity 7	$(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$
Identity 8	$a^3 + b^3 + c^3\;–\; 3abc = (a + b + c)(a^2 + b^2 + c^2 \;–\; ab \;–\; bc \;–\; ca)$

Factorization Identities List

Some of the higher algebraic expressions, like $a^4 \;–\; b^4,\; a^6 \;–\; b^6,\; a^6 + b^6$, etc., can be easily factorized with a collection of algebraic identities that can be used to factor polynomials. The following are some common factorization identities.

Factorization Identities
$a^2 \;–\; b^2 = (a + b)(a \;–\; b)$
$(x + a)(x + b) = x^2 + (a + b)x + ab$
$a^3 \;–\; b^3 = (a \;–\; b)(a^2 + ab + b^2)$
$a^3 + b^3 = (a + b)(a^2 \;–\; ab + b^2)$

Facts about Algebraic Identities

Conclusion

In this article, we have learned about all algebraic identities, proofs, and related facts. Let’s solve a few examples and practice problems based on the list of algebraic identities.

Solved Examples on Algebraic Identities

1. Find the value of $195 \times 205$.

Solution: 

$195 \times 205$ can be written as $(200 \;–\; 5) \times ( 200 + 5)$

Applying $(a + b)(a \;–\; b) = a^2 \;–\; b^2$ with $a = 200$, and $b = 5$, we get

$(200 \;–\; 5) \times ( 200 + 5) = 200^2 \;-\; 5^2$

$= 40000 \;–\; 25$

$= 39975$

2. Using algebraic identities simplify $(5p \;–\; 6q)^2 + (5p + 6q)^2$

Solution: 

The given expression is in the form of $(a \;–\; b)^2 + (a + b)^2$

So, we have to apply the following identities

• $(a + b)^2 = a^2 + 2ab + b^2$
• $(a \;–\; b)^2 = a^2 \;–\; 2ab + b^2$

Here, $a = 5p$, and $b = 6q$

$(5p \;–\; 6q)^2 = (5p)^2 \;–\; 2(5p)(6q) + (6q)^2 = 25p^2 \;–\; 60pq + 36q^2$ … (i)

$(5p + 6q)^2 = (5p)^2 + 2(5p)(6q) + (6q)^2 = 25p^2 + 60pq + 36q^2$ … (ii)

Now adding equations (i) and (ii), we get

  $(5p \;–\; 6q)^2 + (5p + 6q)^2 = 25p^2 \;–\; 60pq + 36q^2 + 25p^2 + 60pq + 36q^2$

                                       $= 2(25p^2 + 36q^2)$

$\therefore (5p \;–\; 6q)^2 + (5p + 6q)^2 = 2(25p^2 + 36q^2)$

3. Using standard algebraic identities, determine the product of $(2k + 4)$ and $(2k + 9)$.

Solution: 

Given multiplication is $(2k + 4) \times (2k + 9)$

Apply $(x + a)(x + b) = x^2 + (a + b)x + ab$

Here $x = 2k,\; a = 4,$ and $b = 9$

So, $(2k + 4) × (2k + 9)  = (2k)^2 + (4 + 9)2k + (4)(9)$

$= 4k^2 + 26k + 36$

4. Using standard identities simplify $(2x \;–\; y)^3 + ( 2x + y )^3$

Solution:

The given expression is in the form of $(a \;–\; b)^3 + (a + b)^3$

So, we have to apply the following identities

• $(a + b)^3 = a^3 + b^3 + 3ab (a + b)$
• $(a \;–\; b)^3 = a^3 \;–\; b^3 \;–\; 3ab (a \;–\; b)$

Here, $a = 2x$, and $b = y$

$(2x \;–\; y)^3 = (2x)^3 \;–\; y^3 \;–\; 3(2x)(y) (2x \;–\; y) = 8x^3 \;–\; y^3 \;–\; 6x^2 y + 6xy^2$ … (i)

$(2x + y)^3 = (2x)^3 + y^3 + 3(2x)(y) (2x + y) = 8x^3 + y^3 + 6x^2y + 6xy^2$ … (i)

Adding equations (i) and (ii), we get

$(2x \;–\; y)^3 + (2x + y)^3 = 8x^3 \;–\; y^3 \;–\; 6x^2 y + 6xy^2 + 8x^3 + y^3 + 6x^2 y + 6xy^2$

                                $= 2(8x^3 + 6xy^2) = 4(4x^3 + 3xy^2)$

$\therefore (2x \;–\; y)^3 + (2x + y)^3 = 4(4x^3 + 3xy^2)$

5. Using factorization identities, factorize $(8x^3 + 27y^3)$.

Solution:

The given expression can be written as $(8x^3 + 27y^3) = (2x)^3 + (3y)^3$, 

which is in the form of $a^3 + b^3$

So, for factorization we have to apply the identities $a^3 + b^3 = (a + b)(a^2 \;–\; ab + b^2)$

Here, $a = 2x$ and $b = 3y$

Now

$(8x^3 + 27y^3) = (2x)^3 + (3y)^3$ 

                    $= (2x + 3y)((2x)^2 \;–\; (2x)(3y) + (3y)^2)$

                    $= (2x + 3y)(4x^2 \;–\; 6xy + 9y^2)$

Hence, $(8x^3 + 27y^3) = (2x + 3y)(4x^2 \;–\; 6xy + 9y^2)$

Practice Problems on Algebraic Identities

Frequently Asked Questions on Algebraic Identities