Cardinality of a Set: Definition, Symbol, Examples, Facts, FAQs

Cardinality of a set refers to the total number of elements present in a set. 

The meaning of cardinality in math is the number that describes the size of a set.

Example 1: In the set $A = \left\{2, 3, 4, 6, 8\right\}$, there are 5 elements. Thus, the cardinality is 5. 

Example 2: The cardinality of the set $X = \left\{1, 5, 3, 2, 10, 6, 4\right\}$ is 7 because the set has 7 elements.

Cardinality of a Set: Definition

Cardinality refers to the concept of the “size” or “count” of a set. 

Cardinality of a set can be defined as the number of elements present in the set.

Cardinality Symbols

The cardinality of a set X is denoted by |X|. 

We can also represent the cardinality of the set X as n(X).

• $A = \left\{1, 5, 3\right\}$

$|A| = 3$

• $B = \left\{1, 2, 3, 8, 5, 4\right\}$

$|B| = n(B) = 6$

How to Find the Cardinality of a Set

To find the cardinality of a set, count the number of elements present in the given set. Look at the example given below:

$A = \left\{a, b, c, d, e\right\}$ cardinality of this set is 5 because it has 5 elements present inside the set.

$X = \left\{5, 8, 2, 6, 21, 7\right\}$ cardinality of this set is 6, because it has 6 elements present inside the set.

Cardinality of a Power Set

Power set is the set of all the subsets of the given set. If the set A has “n” number of elements, the cardinality of its power set is 2n . Take a look at the given example:

 $A = \left\{1, 2, 3, 4, 5\right\}$

Cardinality of $P(A) = 2^{5} = 32$

The cardinality of a power set is greater than the cardinality of the given set.

Cardinality of Finite Sets

In a finite set, there are a finite number of elements present in the set. Thus, the cardinality will always be a natural number. Cardinality can be easily written by counting how many elements are present in the set. 

For example, set $A =  \left\{3, 6, 9, 16\right\}$ is a finite set.

Set A has four elements. Thus, the cardinality of set A is 4. 

If $A = \left\{1, 2, 3, 4,\; …., \;100\right\}$, then $n(A)$ (or) $|A| = 100$ and it is a finite set.

Cardinality of Infinite Sets

An infinite set can either be countable or uncountable. Do not confuse the terms “countable” and “uncountable” with “finite” and “infinite.”

There may be infinitely many elements in a set, but if we can define a one-to-one correspondence between the elements of the set with the set of natural numbers, the set is said to be countable. 

The cardinality of the natural numbers is |N| = ℵ0. It is  the first letter from Hebrew language known as “aleph null” or “ℵ0,” which represents the smallest infinite number.

• As a countably infinite set has one-to-one correspondence with the set of natural numbers N, the cardinality of countable infinite set is also denoted by ℵ0.
• An uncountable set has a cardinality of greater than ℵ0.

Cardinality of Countable Sets

We know that natural numbers are also known as counting numbers. It is because we use them for counting things. 

A set X is called a countable set when it satisfies any ONE of following conditions:

• The set X is a finite set. The cardinality of the finite countable set is a total number of elements present in the set. 
• The set X is infinite but there is one-to-one correspondence between the set X and the set of natural numbers N. It tells us whether an infinite set is countable or not. In this case, we have $n(X) = n(N)$. 

If a set is countable and infinite, then it is called a “countably infinite set.” The cardinality of an infinite countable set is equal to the cardinality of the set of natural numbers. Additionally, we also represent the cardinality of countably infinite sets as ℵ0 (“aleph null”).

NOTE:

Here, we are able to count the number of elements theoretically with the help of natural numbers, but we are not actually reaching the end of the set.

The sets like N (natural numbers), Z (integers) and Q (rational numbers) are countably infinite.

Here’s an image to understand what we mean by one-to-one correspondence between the set of integers and the set of natural numbers. Every integer corresponds to only one natural number, and vice versa! This way, we can say that the counting is possible, even if we are not reaching toward the end.

Cardinality of Uncountable Sets

If the elements of the set can’t be counted, then the set is called an uncountable or uncountably infinite set. A finite set is never an uncountable set. A set is uncountable if its cardinality is greater than ℵ0 (the cardinality of the set of natural numbers).

The set of real numbers is an uncountable set. Also, in intervals like  $\left[a, b\right],\; (a, b], [a, b), (a, b)$, in which $a \lt b$, are all uncountable sets.

In this case, there’s no way to establish a one-to-one correspondence between the set and the set of natural numbers. 

Comparing Cardinalities of Sets

Before we begin, let’s discuss two important types of functions:

i) One-to-one function (injective): Each input has a unique (or distinct) output. Each element in the domain (set of valid inputs for a function) maps to a unique element in the codomain (set of possible outputs).

ii) Onto function (surjective): The entire codomain represents the range. Each element in the codomain is mapped to some input. So, in a mapping diagram, some element of the co-domain has no arrow pointing to it.

Now, let us compare cardinalities of two sets A and B (both can be finite or infinite):

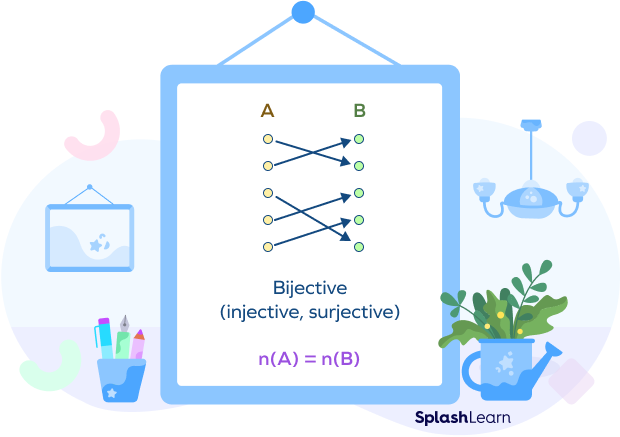
• If there is a bijection (one-one and onto) from $A \Rightarrow B$, then $n(A) = n(B)$ 

In this case, every input has a unique output and also the codomain or the set B represents the range. Every element in B corresponds to exactly one element in A. Thus, $n(A) = n(B)$.

• One-one and may be onto:

In this case, we have a possibility of equality, so we get $n(A) \le n(B)$

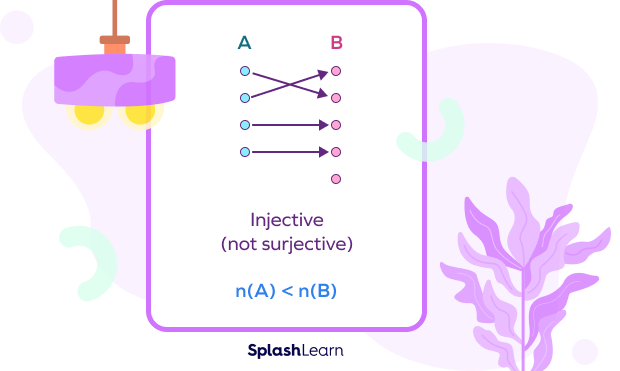
• If there is an injection (only one-one but not onto), then $n(A) \lt n(B)$

Here, every input has a unique output, but a few elements are left in B, which do not correspond to any element in A. In other words, B has at least one extra element than A.

Hence, we can say that $n(A) \lt n(B)$.

Properties of Cardinality of a Set

To understand the cardinality rules and concept, let us learn some important properties of cardinality of a set:

• For any two sets A and B, 

$n(A U B) = n(A) + n (B) \;-\; n (A ∩ B)$

• For any three sets A, B, and C, 

$n(A U B U C) = n (A) + n(B) + n(C) \;-\; n(A ∩ B) \;-\; n(B ∩ C) \;-\; n(C ∩ A) + n (A ∩ B ∩ C)$

• If A and B are two disjoint sets, then 

$n(A U B) = n(A) + n (B)$

• If the sets have the same cardinality, the relation of these sets is called an equivalence relation.

Facts on Cardinality

Conclusion

In this article, we have learned the meaning of cardinality, cardinality of different types of sets and examples for each type. Now, let us practice solving problems on the cardinality of a set.

Solved Examples on Cardinality

1. What is the cardinality of the set of vowels in the English alphabet? 

Solution:

Let X be the set of vowels. 

Thus, it can be written as $X = \left\{a, e, i, o, u\right\}$. 

The set X is finite and has five elements. 

Thus, the cardinality of the set of vowels in the English alphabet is 5.

2. Find the cardinality of the power set of A if $n(A) = 4$.

Solution:

If the set A has n number of elements, then the power set P(A) has $2^{n}$ elements.

$n(A) = 4$

n(P(A)) = 2^{4} = 16$

Thus, the cardinality power set of A is 16.

3. What is the cardinality $P = \left\{\text{Sun, Mon, Tue, Wed, Thu, Fri, Sat}\right\}$? Is the set countable?

Solution:

Given $P = \left\{\text{Sun, Mon, Tue, Wed, Thu, Fri, Sat}\right\}$

P has seven elements. 

Thus, the cardinality of P is 7.

The set is finite, and thus countable.

Practice Problems on Cardinality

Frequently Asked Questions about Cardinality