Cardinal Numbers

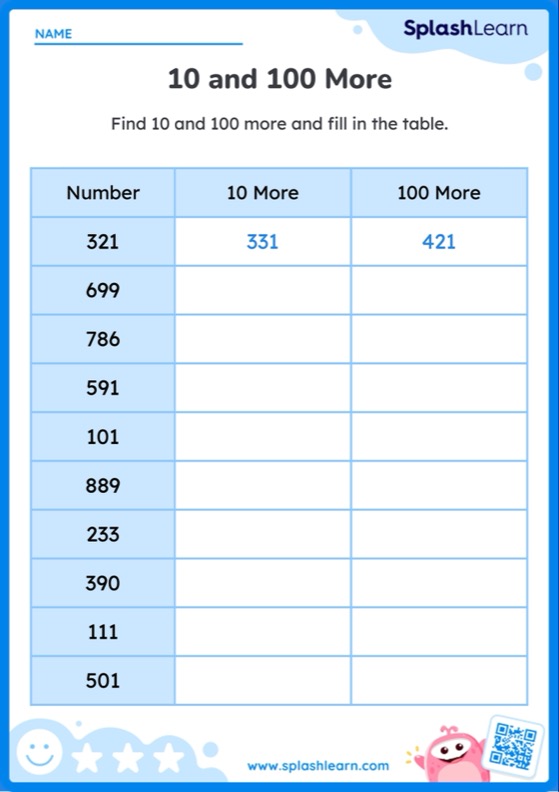
What Are Cardinal Numbers?

Cardinal numbers are numbers that are used for counting real objects or counting things. They are also known as “counting numbers” or “cardinals.”  We commonly use cardinal numbers or cardinals to answer the question starting with “How many?” 

So, how to find the cardinal numbers around us? Let’s see an example.

Example:

How many dogs are in the given picture?

To know the total number of dogs, we need to count the dogs given in the image.

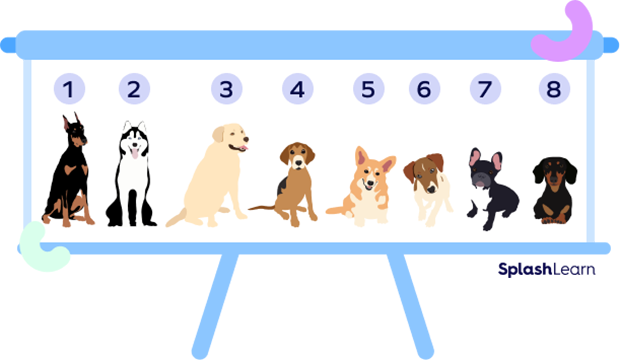
There are 8 dogs in all. Here, 8 is the cardinal number.

Cardinal Numbers: Definition

The numbers that we use for counting are called cardinal numbers. They tell us the quantity of objects.

Cardinal Numbers Examples: 2 bananas, 5 suitcases, 100 points, a million dollars, etc. 

Cardinal numbers do not include fractions or decimals. Cardinal numbers are natural numbers or positive integers. The smallest cardinal number is 1. 

Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on.

The smallest cardinal number is 1.

If we count a bag filled with a million dollars, we get a cardinal number: “one million!”

Example:

Cardinal Numbers in Words

We can also write cardinal numbers in words. For the first 10 numbers, we can write the cardinal numbers as:

• 1 – One
• 2 – Two
• 3 – Three
• 4 – Four
• 5 – Five
• 6 – Six
• 7 – Seven
• 8 – Eight
• 9 – Nine
• 10 – Ten

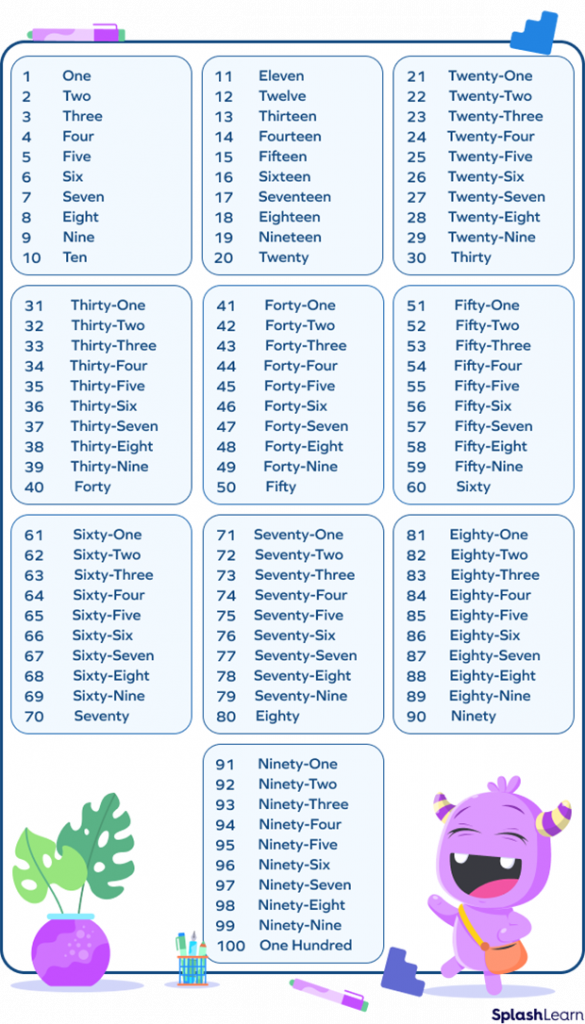
List of Cardinal Numbers

Here’s a list of cardinal numbers up to 100, in figures and in words:

Cardinal Numbers as Multiples of 100:

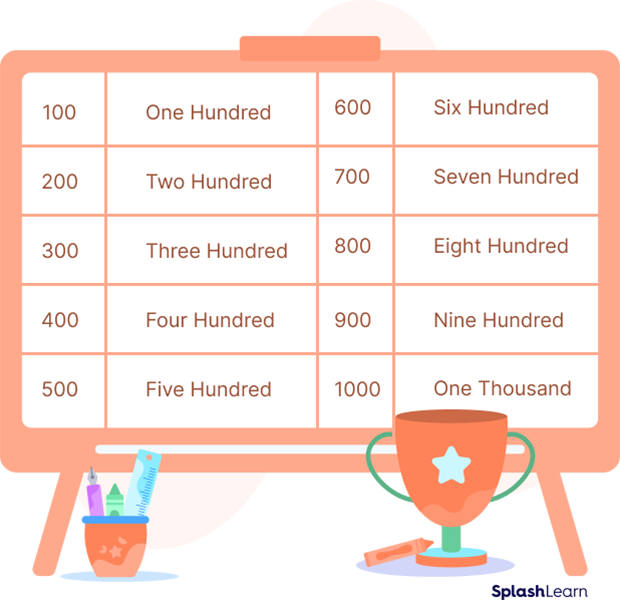
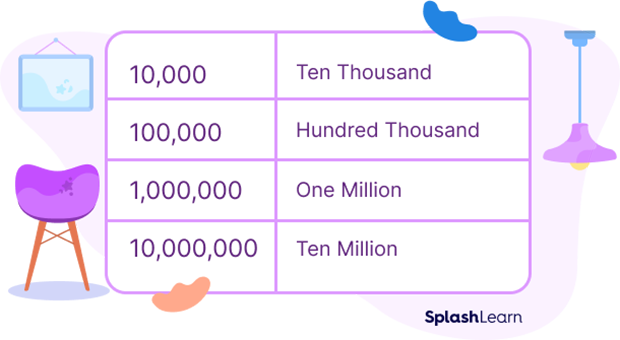
We can count further and list a few larger cardinal numbers as well:

What Is Cardinality?

The cardinality of a group or a set represents how many elements or numbers are present in a group or in a set.

For example, if a pencil set has 10 pencils in it, then the cardinality of pencils is 10.

Cardinal Number of a Set

The number of elements in a set is known as the cardinal number of that set. If A is a finite set and it has N elements, then the cardinal number of set A is given by n(A) $=$ N. 

Note: The cardinal number of an empty set is always zero.

For example, what is the cardinal number of a set if the set is defined as A $=$ {2, 5, 7, 9, 11, 15, 19, 22, 24}?

 The cardinal number of set A is 9. Hence, n(A) $=$ 9

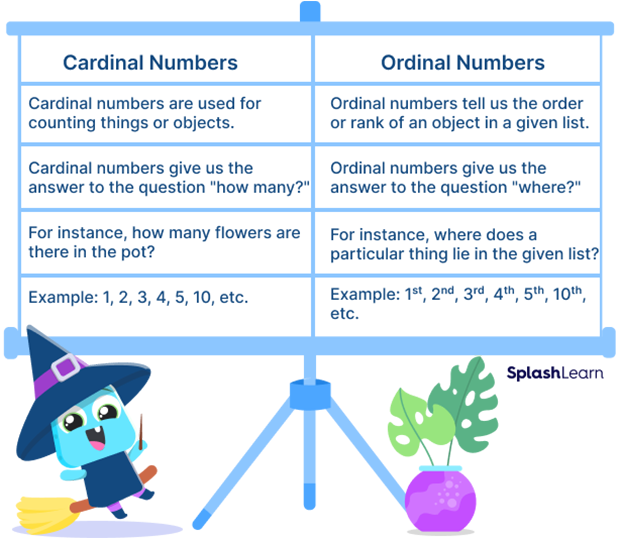
Cardinal Numbers vs. Ordinal Numbers

As we discussed, the cardinal numbers are used for counting. They include all the natural numbers. However, an ordinal number is a number that is used to represent the position or order of an object. Examples:

1^st  rank, 2^nd in a queue, 3^rd row, tenth floor, etc. 

Ordinal numbers are used for ranking or ordering. 

Here’s an example that explain the difference between cardinal and ordinal numbers:

In the image given above, we can see a group of 8 children on the picnic spot. Here, 8 represents the cardinal number.

In the above image, we can see the position of the kids in a running event. Here, first, second, third, fourth, fifth are ordinal numbers. 

 

Difference between Cardinal Numbers and Ordinal Numbers

Nominal Numbers

Nominal numbers, as the name suggests, are used to name an object or a thing in a set of groups. They help us in the identification of objects. It is not used to represent the quantity or the position of an object. 

For example:

• Social security number 
• Zip code number
• Cell phone number

In the image given below, the numbers 22, 18 are nominal numbers since they are used on the jerseys to represent players or to identify players.

Conclusion

In this article, we learnt about the Cardinal Numbers. Cardinal Numbers are the numbers used for counting numbers. To read more such informative articles on other concepts, do visit SplashLearn. We, at SplashLearn, are on a mission to make learning fun and interactive for all students. 

Solved Examples

1. Kathy has a list of numbers as shown: 10, 9, 7^th, 22, Third, Five, 21^st. Identify the cardinal numbers.

Solution: The cardinal numbers are used for counting. The cardinal numbers are 10, 9, 22 and Five.

2. Help Mark calculate the number of consonants in “INDEPENDENCE.” Also identify the number of alphabets used to form this word.

Solution: The consonants are alphabets other than vowels. The vowels are a, e, i, o and u. The number of consonants INDEPENDENCE are 7. The number of alphabets in the word INDEPENDENCE are 12.

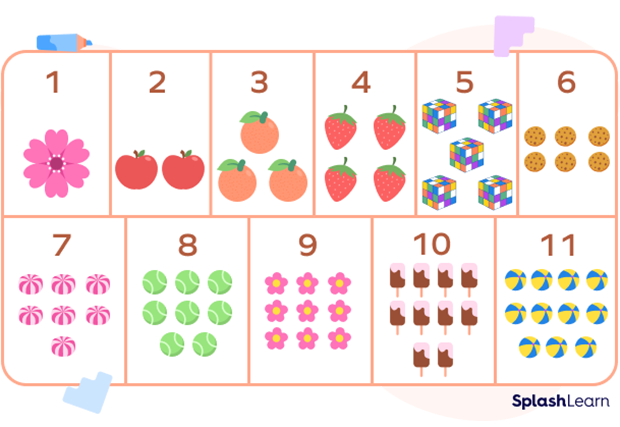
3. Write the cardinality of the flowers in the vase.

Solution: There are 5 flowers in the vase. So, the cardinality is 5.

4. What is the position of the strawberry from the left?

Solution: The strawberry is at the second position from the left. Here, second is the ordinal number.

5. How many kites are there in all? What is a cardinal number here?

Solution: On counting, we get:

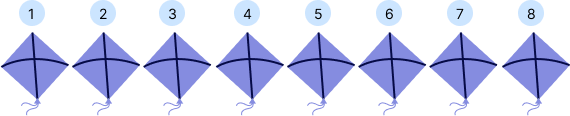
There are 8 kites. 8 is the cardinal number since we used it for counting.

Practice Problems

Frequently Asked Questions