What Are Concentric Circles?
Concentric circles are two or more circles having the same center but different radii.
A circle is a two-dimensional geometric figure which is defined as the collection of all points that are equidistant from a fixed point called the center, and the fixed distance is called the radius of a circle. All circles are similar since they have the same shape but different sizes.
If you draw two circles with different radii keeping the same center, you get concentric circles! Note that circles are not concentric if they have a different center.
Recommended Games
Concentric Circles Definition
Concentric circles are a set of circles with the same center, but different radii such that they appear nested inside one another.
Recommended Worksheets
Equations of Two Concentric Circles
We know that concentric circles have the same center but different radii.
The equation of a circle with center (h, k) and radius r is given by
$(x\;-\;h)^{2} + (y\;-\;k)^{2} = r^{2}$
The equation of a circle with radius $r_{1}$ that is concentric with this circle is given by
$(x\;-\;h)^{2} + (y\;-\;k)^{2} = r_{1}^{2}$
Examples of Concentric Circles Around Us
Some examples of concentric circles in real life are dartboard, ripples made when a stone is dropped in the water, and wheels of a ship.
Here are some concentric circles examples around us!

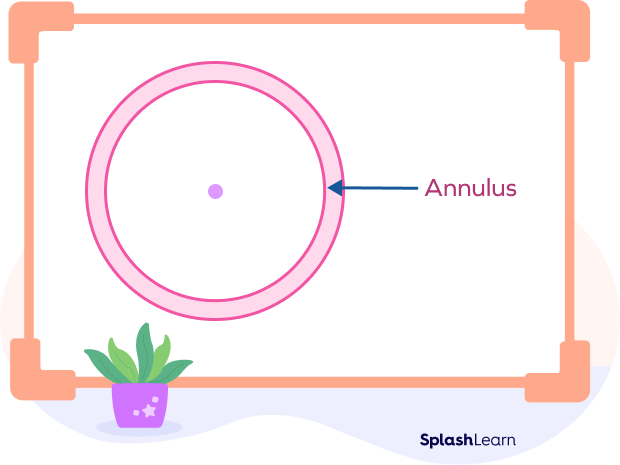
Annulus: The Region Between Concentric Circles
The region which is formed between two concentric circles is known as an annulus. It is shaped like a flat ring or a donut.
The shaded part shows the annulus in the following figure:
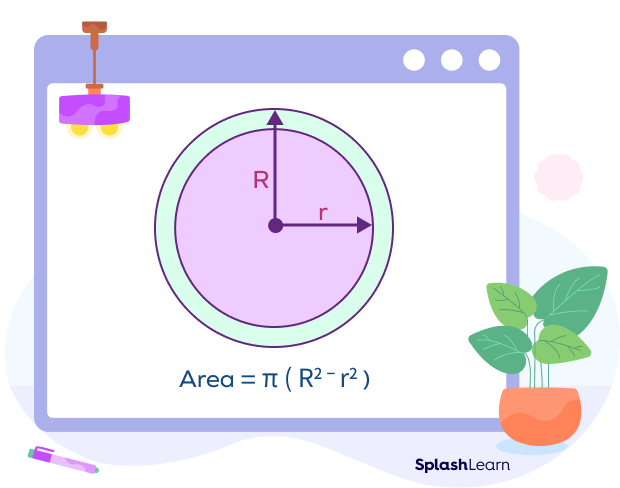
How To Find Area of Annulus
The formula for finding the area of the annulus is:
Area $= \pi (R^{2}\;-\;r^{2})$
where
R: radius of outer circle
R: radius of inner circle
Derivation of Area of Annulus
Let the radius of smaller i.e., orange circle be r units and radius of the bigger circle be R units.
Area of the smaller circle $= \pi r^{2}$
Area of the bigger circle $= \pi R^{2}$
Area of annulus = Area of bigger circle – Area of smaller circle
Area of annulus $=\pi R^{2}\;-\;r^{2}$
Area of annulus $= (R^{2} \;-\; r^{2})$
Concentric Circles – Theorem
Statement: In two concentric circles, if the chord of the larger circle is a tangent to the smaller circle (touches the smaller circle), then it is bisected at the point of contact.
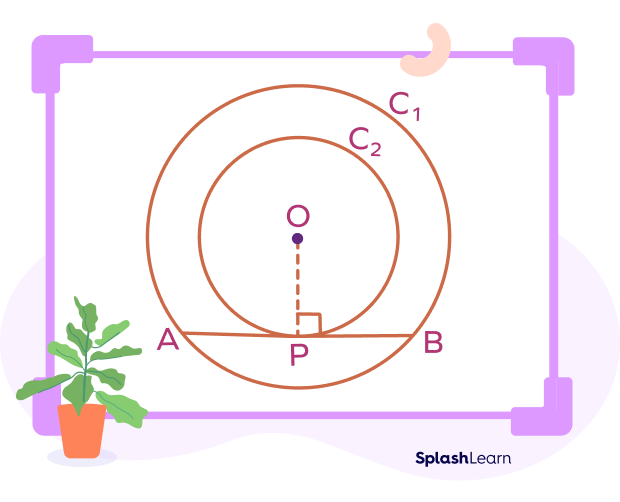
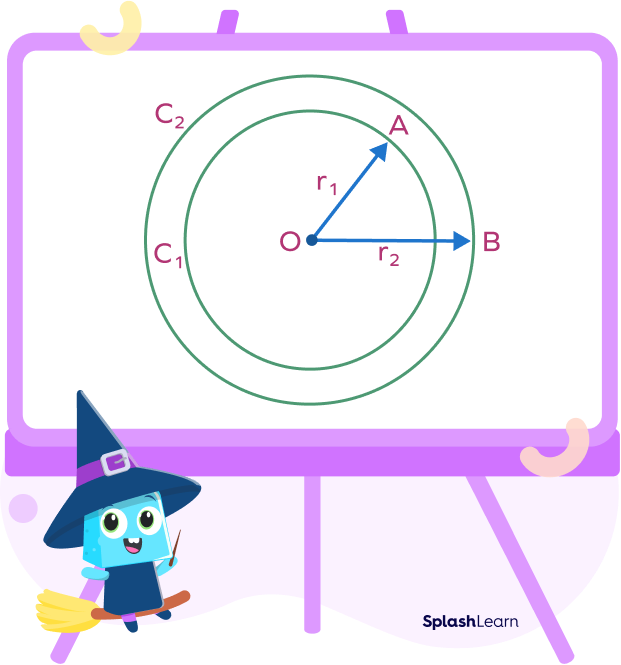
Given: Consider two concentric circles $C_{1}$ and $C_{2}$, with center O and a chord AB of the larger circle $C_{1}$, touching the smaller circle $C_{2}$ at the point P
Construction: Join OP.
To prove: AP = BP
Proof:
AB is the chord of larger circle $C_{1}$. It is a tangent to $C_{2}$ at point P.
OP is the radius of circle $C_{2}$.
We know that the radius is perpendicular to the tangent at the point of contact.
So, OP ⊥ AB
Now, AB is a chord of the circle $C_{1}$ and OP ⊥ AB.
We know that the perpendicular from the center of a circle bisects the chord.
Hence, OP is the bisector of the chord AB.
Thus, AP = BP.
What Are Concentric Objects?
The objects are said to be concentric if they share a common center. Polygons, circles, spheres etc are said to be concentric when they share the same center point.

Conclusion
In this article, we learned about concentric circles, which are circles that share the same center point but have different radii. Understanding their properties helps us analyze geometric relationships. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Concentric Circles
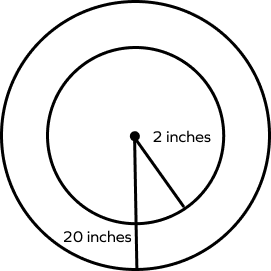
1. Draw two concentric circles with the center O such that the radius of the smaller circle is 2 inches and the radius of the bigger radius is 5 inches.
Solution:
2. Find the width of the annulus if the radius of the bigger circle is 8 feet and the radius of the smaller circle is 5 feet.
Solution:
Radius of the bigger circle (R) = 8 feet
Radius of the smaller circle (r) = 5 feet
Width $= R\;-\;r = 8\;-\;5 = 3$ feet
3. If the width of annulus is 7 inches and the radius of the bigger circle is 12 inches, then what is the radius of the smaller circle?
Solution:
Radius of the bigger circle (R) = 12 inches
Width of the annulus = 7 inches
Radius of the smaller circle (r) = 12 – 7 = 5 inches
4. Find the area of the shaded region.
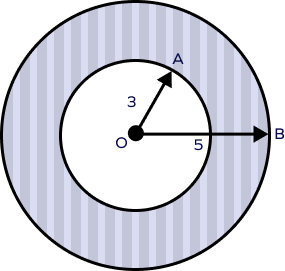
Solution:
Radius of outer circle (R) = 5 units
Radius of inner circle (r) = 3 units
Area of the path $= (R^{2} \;-\; r^{2})$
$= \frac{22}{7} \times (5^{2}\;-\;3^{2})$
$= \frac{22}{7} \times (25\;-\;9)$
$= \frac{22}{7} \times 16$
= 50.28 square feet
5. If the area of annulus is 2618 square inches and the radius of the smaller circle is 56 inches, then what is the radius of the bigger circle?
Solution:
Area of the annulus = 2618 square inches
Radius of smaller circle (r) = 56 inches
Let the radius of bigger circle be R inches.
Area of the annulus $= \pi (R^{2}\;-\;r^{2})$
$2618 = \frac{22}{7} \times (R^{2} \;-\; 56^{2})$
$2618 \times \frac{7}{22} = R^{2}\;-\;56^{2}$
$833 = R^{2}\;-\;3136$
$R^{2} = 833 + 3136$
$R^{2} = 3969$
R=63 inches
Practice Problems on Concentric Circles
Concentric Circles - Definition, Equation, Facts, Examples, FAQs
Two circles are said to be concentric if they have a common ____.
Two circles are said to be concentric if they have a common center.
What is the width of the annulus in the following figure?
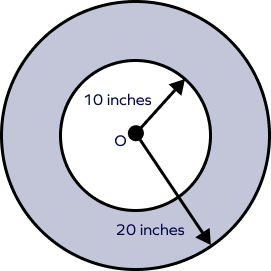
Width of annulus = 20 – 10 = 10 inches
What is the area of annulus if the outer and inner radii are 15 inches and 8 inches respectively?
Outer radii (R) = 15 inches
Inner radii (r) = 8 inches
Area of annulus $= \pi (R^{2}\;-\;r^{2}) = \frac{22}{7} \times (15^{2}\;-\;8^{2}) = \frac{2}{27} \times (225\;-\;64) = \frac{22}{7} \times 181 = 504$ square inches
Frequently Asked Questions about Concentric Circles
Do concentric circles have the same perimeter?
No, the concentric circles do not have the same perimeter since their radii are different.
What is the difference between concentric and congruent circles?
Concentric circles are the circles that share the common center and congruent circles are the circles that have the same radii.
How To Draw Concentric Circles?
You can draw concentric circles diagram using a compass, keeping the same center but taking two different radii.
What is the difference between concentric circles and eccentric circles?
Concentric Circles are the circles that share a common center. On the other hand, eccentric circles are the circles that do not share the common center and do not intersect also.



















