What Are Concurrent Lines in Geometry?
Concurrent lines are three or more lines meeting exactly at a single point.
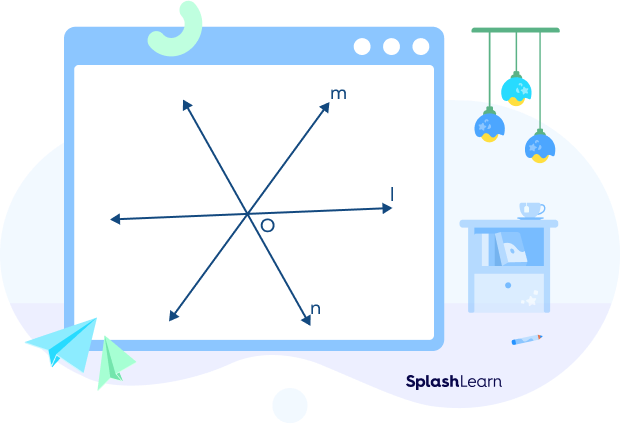
We know that two lines can intersect at one point only. What if there are three or more lines meeting at a single point? Take a look at the image below. The lines l, m, and n intersect each other at a single point, O. Thus, lines l, m, and n are concurrent.
Recommended Games
Concurrent Lines: Definition
Three or more lines that intersect at one common point are said to be concurrent lines.
When two lines meet each other, they are said to be intersecting. When a third line passes through the point of intersection made by the first two lines, then these three lines are known as the concurrent lines.
What Is the Point of Concurrency?
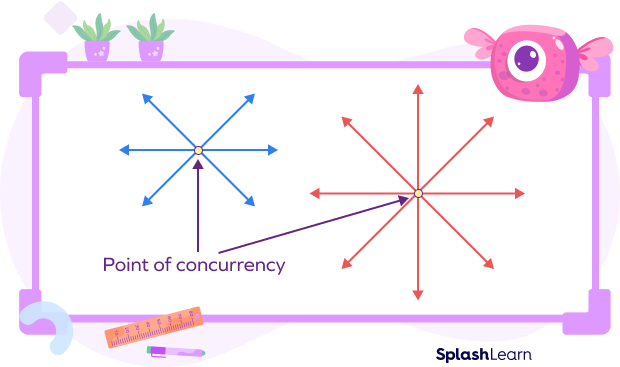
The point of intersection of three or more lines is known as the “point of concurrency.” It is the point where three or more lines meet.
Concurrent lines examples:
Condition for Concurrent Lines (Concurrent Lines Formula)
If three lines are concurrent, then the point of intersection of two lines satisfies the equation of the third line (i.e., it lies on the third line).
Consider three lines whose equations are:
$a_{1} x + b_{1} y + c_{1} = 0$ ……………. (1)
$a_{2} x + b_{2} y + c_{2} = 0$ ……………. (2)
$a_{3} x + b_{3} y + c_{3} = 0$ ……………. (3)
If the determinant of the coefficients is 0, then the lines are concurrent. Thus, the condition for the lines to be concurrent is

How to Know if Lines Are concurrent
How can we know if the given lines are concurrent? There are two methods to find if three lines are concurrent or not:
Method 1: Determinant Method
If the three lines are concurrent, then the determinant of coefficients is 0. Thus, the lines should follow the condition for concurrent lines.
Suppose, the equation of three lines are:
$2x \;–\; 3y + 5 = 0$
$3x + 4y \;–\; 7 = 0$
$9x \;–\; 5y + 8 = 0$
Determinant $D = 2(32 \;–\; 35) \;-\; (\;-\;3)(24 + 63) + 5(\;-\;15 \;–\; 36)$
$= 2(\;-\;3) + 3(87) + 5(\;-\;51)$
$= \;–\; 6 + 261 \;-\;255$
$= 0$
Hence, the lines are concurrent.
Method 2: Solving the Equations
Here, we first find the point of intersection of two lines and then check if the point lies on the third line. It ensures that all three lines are concurrent.
Consider equations of three lines.
$2x \;-\; 3y + 5 = 0$ —–(1)
$3x + 4y \;-\; 7 = 0$ —–(2)
$9x \;-\; 5y + 8 = 0$ —–(3)
Solving (1) and (2) by making the coefficient of x equal.
$6x \;-\; 9y + 15 = 0$
$6x + 8y \;-\; 14 = 0$
Subtracting, we get
$17y = 29$
$y = \frac{29}{17}$
Putting the value of $y = \frac{29}{17}$ in the equation $6x \;-\; 9y + 15 = 0$, we get the value of “x.”
$6x \;-\; 9(\frac{29}{17}) + 15 = 0 =$
$6x = \frac{261}{17} \;-\; 15 = \frac{6}{17}$
Thus, $x = \frac{1}{17}$
Therefore, line 1 and line 2 intersect at a point $(\frac{1}{17},\; \frac{29}{17})$.
Substitute the point of intersection of the first two lines in the equation of the third line.
Equation of the third line is $9x \;-\; 5y + 8 = 0$.
Substituting the values of (4,6) in the equation (3), we get
$9x \;-\; 5y + 8 = 9(\frac{1}{17})\;-\; 5(\frac{29}{17}) + 8$
$= \frac{9}{17} \;-\; \frac{145}{17} + \frac{136}{17}$
$= 0$
The point satisfies the equation of the third line.
Hence, these are concurrent lines.
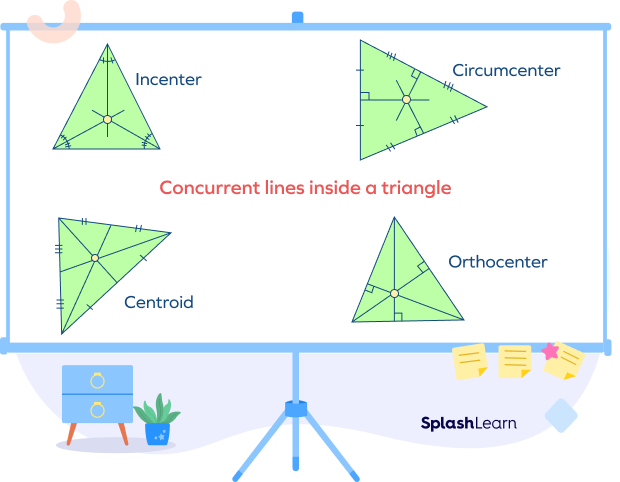
Concurrent Lines in Triangles
Concurrent lines can be found in triangles when special types of line segments are drawn inside a triangle. In a triangle, the four important types of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors. Thus, there are four different points of concurrency.
- Incenter: The point of intersection of three angle bisectors of a triangle is known as the incenter of a triangle.
- Circumcenter: The point of intersection of three perpendicular bisectors of a triangle is known as the circumcenter of a triangle.
- Centroid: The point of intersection of three medians of a triangle is known as the centroid of a triangle
- Orthocenter: The point of intersection of three altitudes of a triangle is known as the orthocenter of a triangle.
Concurrent Lines in Geometry
Let’s see some examples of concurrent lines in different geometric shapes.
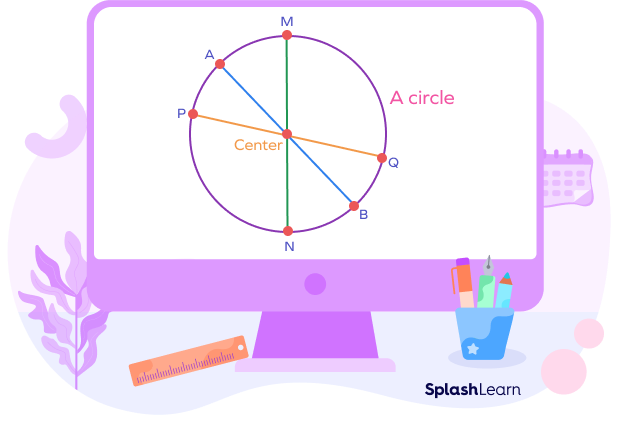
Circles
The diameters of a circle are concurrent such that the point of concurrency is the center of the circle.
Quadrilaterals
In quadrilaterals, the line segments joining the midpoints of opposite sides, and the two diagonals are concurrent lines.
Difference between Concurrent Lines and Intersecting Lines
| Concurrent Lines | Intersecting Lines |
|---|---|
| Three or more lines that pass through a single point in a plane are called concurrent lines. | Two lines meeting at a single point are called intersecting lines. |
| The point where the concurrent lines meet is called the point of concurrency. | The point where two intersecting lines meet is called the point of intersection. |
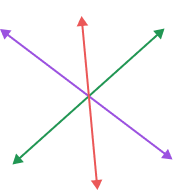 | 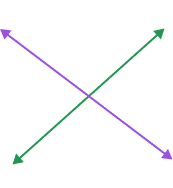 |
Facts about Concurrent Lines
- Parallel lines are not concurrent at any point on a plane.
- In geometry, the concept of concurrent lines is essential, and they play a significant role in various proofs and constructions involving angles, triangles, and other geometric shapes.
- The point of concurrency of three perpendicular bisectors in a triangle is the circumcenter.
- The point of concurrency of three angle bisectors in a triangle is the incenter.
- The point of concurrency of three medians in a triangle is the centroid.
- The point of concurrency of three altitudes in a triangle is the orthocenter.
- In a triangle, the three medians, altitudes, angle bisectors, and perpendicular bisectors are examples of concurrent lines.
Solved Examples on Concurrent Lines
1. Which lines are concurrent in the given figure? Also, tell the point of concurrency.
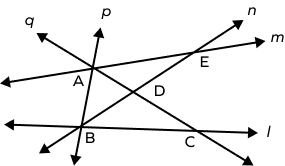
Solution:
Lines p, q, and m are concurrent at point A.
Lines l, p, and n are concurrent at point B.
2. Name all the pairs of concurrent lines and the point of concurrency in the following figure.
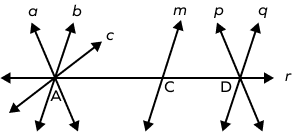
Solution:
Lines a, b, c, and r are concurrent at point A.
Lines p, q, and r are concurrent at point D.
3. Check whether the lines are concurrent or not using the determinant method.
$3x \;-\; 4y \;-\; 13 = 0$
$8x \;-\; 11 y \;-\; 33 = 0$
$2x \;-\; 3y \;-\; 7 = 0$
Solution:
Condition for concurrent lines is
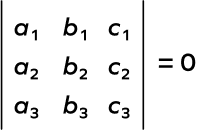
Substitute the values.

Solve the determinant.
$D = 3(77\;-\;99)\;-\;(\;-\;4)(\;-\;56 + 66)\;-\;13(\;-\;24 + 22)$
$D = 3 \times (\;-\;22) + 4 \times 10\;-\;13 \times (\;-\;2)$
$D = \;-\;66 + 40 + 26 = 0$
Hence, the lines are concurrent.
5. Check whether the lines are concurrent or not?
$x + 2y \;-\; 4 = 0,\; x\;-\; y \;-\; 1 = 0,\; 4x + 5y \;-\; 13 = 0$
Solution:
Let us first consider the first two equations.
$x + 2y \;-\; 4 = 0$ –(1)
$x\;-\; y \;-\; 1 = 0$ –(2)
Subtracting (1) and (2)
$x + 2y\;-\;4\;-\;(x\;-\;y\;-\;1) = 0$
$x + 2y\;-\;4\;-\;x + y + 1 = 0$
$2y + y\;-\;4 + 1 = 0$
$3y\;-\;3 = 0$
$y = 1$
Substituting value of $y = 1$ in (2)
$x\;-\;y\;-\;1 = 0\Rightarrow x\;-\;1\;-\;1 = 0$
$x\;-\;2 = 0\Rightarrow x = 2$
The two lines intersect at the point (2,1).
Substituting values of x and y in $4x + 5y \;-\; 13 = 0$, we get
$(4 \times 2) + (5 \times 1)\;-\; 13 = 8 + 5 \;-\; 13 = 0$
Hence, the lines are concurrent.
Practice Problems on Concurrent Lines
Concurrent Lines - Definition, Formula, Examples, FAQs
The lines p, q, and s are ______.
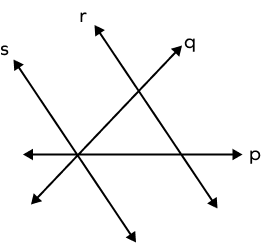
The lines p, q, and s are concurrent lines.
If the determinant of the three lines is 0, then the lines are _________.
If the determinant of three lines is zero, then the lines are concurrent.
If the lines $2x + y \;–\; 3 = 0,\; 5x + ky \;–\; 3 = 0$ and $3x \;–\; y \;–\; 2 = 0$ are concurrent, find the value of k.
$2x + y \;–\; 3 = 0$ – (1)
$5x + ky \;–\; 3 = 0$ – (2)
$3x \;–\; y \;–\; 2 = 0$ – (3)
Adding (1) and (3)
$2x + y \;–\; 3 + 3x \;–\; y \;–\; 2 = 0$
$5x = 5$
$x = 1$
Substituting the value of $x = 1$ in (1)
$2(1) + y\;-\;3 = 0$
$y = 1$
Substituting the values of x and y in (2)
$5(1) + k(1) \;–\; 3 = 0$
$k = \;-\;2$
Which of the following are concurrent lines in triangles?
In a triangle, medians, perpendicular bisectors and angle bisectors are concurrent lines.
Frequently Asked Questions on Concurrent Lines
Are parallel lines concurrent?
No, parallel lines are not concurrent lines, because they do not intersect each other.
What is the difference between intersecting lines and concurrent lines?
Two lines are said to be intersecting lines if they meet at a common point whereas three or more lines are said to be concurrent lines if they meet at a common point.
What are collinear points?
Collinear points are the points that lie on the same line.
Are concurrent lines coplanar?
Yes, concurrent lines are coplanar as they intersect at the same plane.


























