What Is the Decimal to Hexadecimal Conversion?
The decimal to hexadecimal conversion is used to convert a decimal number (base-10 number) into its hexadecimal (base-16) equivalent.
What Is the Hexadecimal Number System?
The base of the hexadecimal system as 16. The 16 symbols used in this system are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Here, the place values are defined in terms of the powers of 16.
What Is the Decimal Number System?
Decimal Number System is a base-10 number system that uses ten digits from 0 to 9. Here, the place values are defined in terms of powers of 10.
Decimal to hexadecimal conversion is carried out by successive division by 16. It is a simple and straightforward method. Let’s learn.
Recommended Games
Decimal to Hexadecimal Table
The table shows the hexadecimal numbers equivalent to the decimal numbers from 0 to 15. This decimal to hexadecimal chart is extremely useful for the decimal to hexadecimal conversion.
| Decimal Number | Hexadecimal Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Recommended Worksheets
How to Convert Decimal to Hexadecimal
Step 1: Divide the number by 16. Note down the quotient and remainder.
If the quotient is 0, the remainder is the equivalent hexadecimal number.
If the quotient is not 0, go to step 2.
Step 2: Divide the quotient in step 1 by 16. Again, note down the quotient and remainder.
If the quotient is 0, write the remainders in reverse order to find the hexadecimal number.
If the quotient is not 0, repeat the process until we get 0 as a quotient.
(Note that when the remainder is greater than 9, we refer to the decimal to hexadecimal table mentioned above to write its hexadecimal equivalent. Replace 10, 11, 12, 13, 14, 15 by A, B, C, D, E, F respectively.)
Example 1: Find the hexadecimal equivalent of (152)10.
| Division | Quotient | Remainder |
|---|---|---|
| $152 \div 16$ | 9 | 8 |
| $9 \div 16$ | 0 | 9 |
Write the remainders in reverse order.
(152)10 = (98)16
Example 2: Convert from decimal to hexadecimal: 45010
| Division | Quotient | Remainder (decimal value) | Remainder(Hexadecimal value) |
|---|---|---|---|
| $450 \div 16$ | 28 | 2 | 2 |
| $28 \div 16$ | 1 | 12 | C |
| $1 \div 16$ | 0 | 1 | 1 |
Writing the remainders in the reverse order, we get
45010 = (1C2)16
Example 3: Convert to hexadecimal: 99910
You can also show the division using columns.
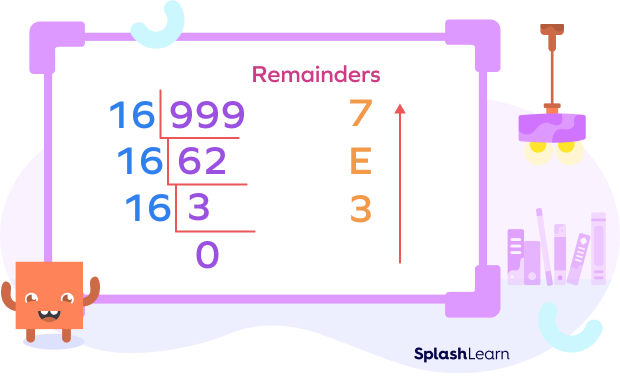
99910 = 3E716
Decimal to Hexadecimal Conversion Involving the Decimal Point
If the decimal number has a fractional form, we convert the integer part and the fractional part to a hexadecimal system separately, and finally add them together.
To convert the fractional value into the hexadecimal system, we multiply the fractional part by 16 and note down the product as the sum of integer value and fractional part.
We repeat the process until the fractional part becomes 0. If the fractional part does not become 0, stop when you get the desired number of digits.
The integer part obtained in every step is written in the same order to get the answer.
The obtained result is the hexadecimal number of the given fractional number.
Example 1: Convert 0.2510 into hexadecimal.
Here, the whole number part is 0. Let’s convert the fractional part into hexadecimal.
0.25 × 16 = 4 + 0.00
Fractional part is 0 in the first step.
Thus, 0.2510 = 0.416
Example 2: Convert 16.22510 into the hexadecimal system.
i) Whole number part = 1610 = 1016
ii) Fractional part = 0.225
0.225 × 16 = 3 + 0.600
0.600 × 16 = 9 + 0.600
0.600 × 16 = 9 + 0.600
We stop here since the process will keep going forever.
0.225 = (0.399…)16
Thus, 16.22510 = (10.3999…)16
Example 3: 15.510
i) Whole number part = 1510 = F16 (from the table)
ii) Fractional part = 0.5
0.5 × 16 = 8 + 0.0
Thus, 0.510 = 0.816
Finally, 15.510 = F.816
Facts about Decimal to Hexadecimal System
- The use of letters A to F in the hexadecimal number system helps in the short and concise symbolic representation of large numbers.
- The prefix “0x” is often used to indicate that a number is written in hexadecimal form, for example, 0xF, 0x5C2.
Conclusion
In this article, we learned about decimal to hexadecimal conversion, how to use the conversion table, and the steps for the conversion. We also learned how to convert a decimal number with fractional or decimal part into a hexadecimal number. Let’s solve a few examples and practice problems based on the decimal to hexadecimal conversion.
Solved Examples on Decimal to Hexadecimal
1. Convert (243)10into a hexadecimal system.
Solution:
Divide 243 by 16 until the quotient is 0.
| Division | Quotient | Remainder (decimal value) | Remainder(hexadecimal value) |
|---|---|---|---|
| $243 \div 16$ | 15 | 3 | 3 |
| $15 \div 16$ | 0 | 15 | F |
Writing remainders in reverse order, we get
So, (243)10 = (F3)16
2. Convert (679)10 into a hexadecimal system.
Solution:
Divide 679 repeatedly by 16 until the quotient becomes 0.
| Division | Quotient | Remainder (decimal value) | Remainder(hexadecimal value) |
|---|---|---|---|
| $679 \div 16$ | 42 | 7 | 7 |
| $42 \div 16$ | 2 | 10 | A |
| $2 \div 16$ | 0 | 2 | 2 |
Write remainders in reverse order to find the answer.
So, (679)10 = (2A7)16.
3. Convert (136)10into a hexadecimal system.
Solution:
| Division | Quotient | Remainder (decimal value) | Remainder(hexadecimal value) |
|---|---|---|---|
| $136 \div 16$ | 8 | 8 | 8 |
| $8 \div 16$ | 0 | 8 | 8 |
Write remainders in reverse order to find the answer.
So, (136)10 = (88)16.
4. What is the value of (2761)10into a hexadecimal system?
Solution:
| Division | Quotient | Remainder (decimal value) | Remainder(hexadecimal value) |
|---|---|---|---|
| $2761 \div 16$ | 172 | 8 | 9 |
| $172 \div 16$ | 10 | 12 | C |
| $10\div 16$ | 0 | 10 | A |
Write remainders in reverse order to find the answer.
So, (2761)10 = (AC9)16.
5. Convert (548.5)10into the hexadecimal system.
Solution:
First, convert 548 into the hexadecimal system.
| Division | Quotient | Remainder (decimal value) | Remainder(hexadecimal value) |
|---|---|---|---|
| $548 \div 16$ | 34 | 4 | 4 |
| $34 \div 16$ | 2 | 2 | 2 |
| $2 \div 16$ | 0 | 2 | 2 |
So, (548)10 = (224)16.
Next, we convert (0.5)10 into the hexadecimal system.
0.5 × 16 = 8 + 0.0
Thus, (0.5)10 = (0.8)16
Adding the whole number part and the fractional part, we get
(548.5)10 = (224.8)16
6. Convert 50 from decimal to hexadecimal.
Solution:
| Division | Quotient | Remainder (decimal value) |
|---|---|---|
| $50 \div 16$ | 3 | 2 |
| $3 \div 16$ | 0 | 3 |
Thus, (50)10 = (32)16
Practice Problems on Decimal to Hexadecimal
Decimal to Hexadecimal Converter: Table, Formula, Examples, FAQs
On converting $(897)_{10}$ in hexadecimal system, we get:
When 897 is divided by 16, the quotient is 56 and remainder is 1.
When 56 is divided by 16, the quotient is 3 and remainder is 8.
When 3 is divided by 16, the quotient is 0 and the remainder is 3.
Writing remainders in reverse order, we get
$(897)_{10} = (381)_{16}$
Convert $(10)_{10}$into a hexadecimal system.
The hexadecimal number system uses the letters A to F for the numbers 10 to 15 respectively.
$(10)_{10} = (A)_{16}$
On converting $(652)_{10}$ in hexadecimal system, we get:
When 652 is divided by 16, the quotient is 40 and the remainder is 12 which is $C_{16}$.
When 40 is divided by 16, the quotient is 2 and the remainder is 8.
When 2 is divided by 16, the quotient is 0 and the remainder is 2.
Writing remainders in reverse order, we get
$(652)_{10} = (28C)_{16}$
What will we get if we convert $(1147)_{10}$into a hexadecimal system?
When 1147 is divided by 16, the quotient is 71 and the remainder is 11, which is $B_{16}$.
When 71 is divided by 16, the quotient is 4 and the remainder is 7.
When 4 is divided by 16, the quotient is 0 and the remainder is 4.
Writing remainders in reverse order, we get
$(1147)_{10} = (47B)_{16}$
What is the value of $(3452)_{10}$into a hexadecimal system?
When 3452 is divided by 16, the quotient is 215 and the remainder is $12 = C_{16}$.
When 215 is divided by 16, the quotient is 13 and the remainder is 7.
When 13 is divided by 16, the quotient is 0 and the remainder is $13 = D_{16}$.
Writing remainders in reverse order, we get
$(3452)_{10} = (D7C)_{16}$
Frequently Asked Questions about Decimal to Hexadecimal Conversion
What is the base of the hexadecimal number system?
The base of a hexadecimal system is 16.
Can I convert a fraction or decimal fraction to hexadecimal?
We use the base of a hexadecimal system as 16. Each digit is 16 times more significant than the previous digit. We use the base of a binary system as 8. Each digit is 8 times more significant than the previous digit.
How do you convert from hexadecimal to decimal?
Multiply each digit with the powers of 16 starting from the ones place of the number.
Example: C216 = 2 160+C161
C216 = 2 160+12161
C216 = 2 +1216
C216 = 2 +192C216 = 19410
What is hex FFFF in decimal?
Hexadecimal notation FFFF equals 65535 in decimal value.
FFFF = 15 163+15162 + 15 161+15160
FFFF = 61440 + 3840 + 240 + 15FFFF = 6553510
What is the decimal to hexadecimal formula?
The decimal to hexadecimal conversion involves dividing the decimal number by 16 and noting the remainders, then assigning hexadecimal equivalents. Reversing the remainders gives the hexadecimal representation.




































