Division Property of Equality – Definition With Examples

The division property of equality tells us that if we divide both sides of an equation by the same number, the equation remains the same.

Suppose you have two pizzas of the same size. You cut each of them into halves and give away one-half from each pizza to your friends. If you measure the remaining portions, you will find that you are left with equal portions from both pizzas.

Here, the initial equation was that both the pizzas were equal. Then you divided them by 2 and found that they are still equal. This means the equation remained the same even when you divided both sides of the equation by a common number.

This is the basic concept of the division property of equality

Division Property of Equality Definition

The division property of equality states that if both sides of an equation are divided by a common real number that is not equal to 0, the quotients remain equal.

The formula for the same can be written as follows:

If a, b, and c are real numbers where a = b and c ≠ 0, then:

$\frac{a}{c}=\frac{b}{c}$

This property is true for all real numbers and even algebraic expressions using variables.

Here is an example of division property of equality using whole numbers.

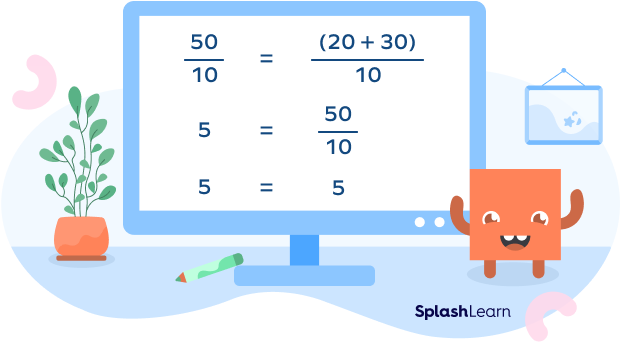
Example 1: Consider the equation 50 = 20 + 30.

Let us divide both sides by 10.

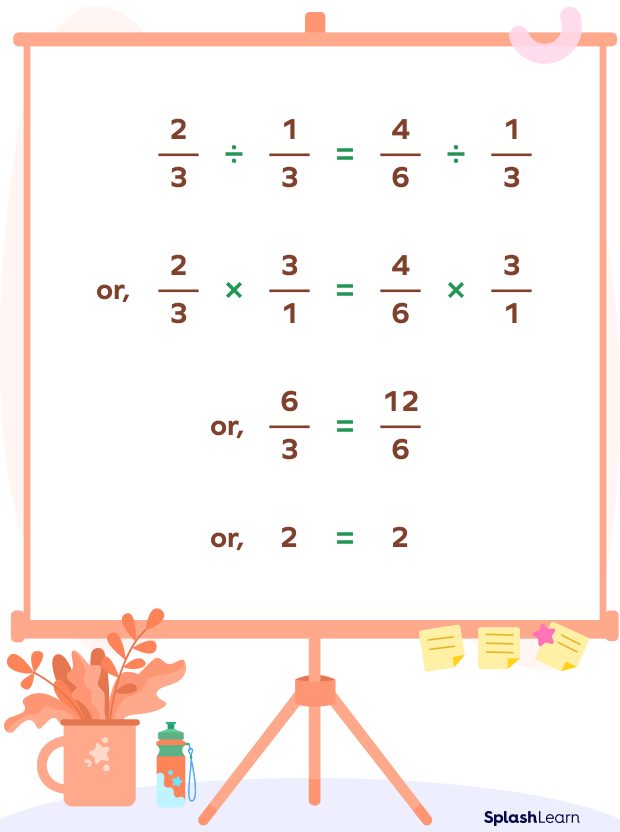
Here is an example using fractions.

Example 2: Let us take the equation 2/3 = 4/6

If we divide both sides by 1/3, we get 

The Inverse of Division Property: Multiplication Property of Equality

The inverse of division property is the multiplication property of inequality. It states that if you multiply the two sides of an equation by any number, the result remains the same. That is, if a, b, and c are any three real numbers and a = b, then this means,

How Is the Division Property of Equality Used?

This property is used in various mathematical contexts.

• This property helps identify whether or not two expressions in arithmetic are equivalent.
• It is used in algebra to solve an unknown variable.

For example:
Let’s say Mia bought 5 cupcakes for $\$$30. How can she find out the price of one cupcake?

Let’s say the price of one cupcake is z dollars.
Therefore, 5z = $\$$30.
Dividing both sides of this equation by 5, we get,

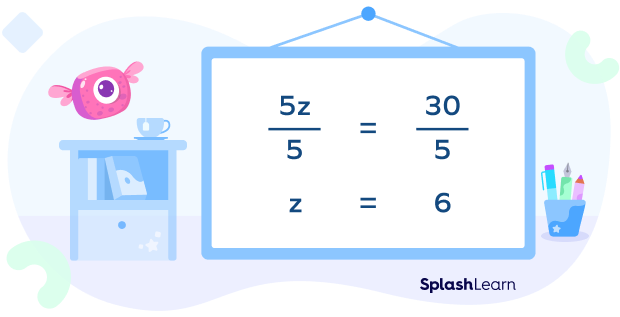
Therefore, each cupcake costs $\$$6.

• It serves as the foundation for the study of logic.

Solved Examples

Example 1: James can store 50 balls in a basket. If he has 300 balls, how many baskets will he need to store them?

Solution: The total number of balls that James needs to store is 300.

Let us say he needs “x” baskets to store the balls.

We form the equation as 50x = 300.

Dividing both sides of the equation by 5, we get,

 $\frac{50x}{5}= \frac{300}{5}$ 

Or, 10x= 60 

Dividing both sides of the equation by 10,

 $\frac{10x}{10}= \frac{60}{10}$,

Or x= 6 .

So, James needs 6 baskets to store 300 balls.

Example 2: Harry covers 56 km in 7 days on his bicycle. Use the division property of equality to find the distance covered by Harry each day.

Solution: Let us say Harry covers “x” km on his bike in one day.

We form the equation as 7x = 56.

Dividing both sides of the equation by 7, we get,

 $\frac{7x}{7}= \frac{56}{7}$

Or, x= 8 

Thus, we see that Harry rides his bike for 8 kms every day. 

Example 3: Find the value of y in the following equation:

11 – 38 = 3y

Solution: We start by simplifying the terms on each side.

11 – 38 = 3y

Or, – 27 = 3y

Dividing both sides of the equation by 3, we get

 $-\frac{27}{3}= \frac{3y}{3}$

Or, $y= –9$

Practice Problems

Frequently Asked Questions