Partial Quotient – Definition, Facts, Examples, FAQs

What Is a Partial Quotient?

A partial quotient refers to a division strategy that uses repeated subtraction to perform the division of large numbers easily.

The partial quotient method is used in long division to break down a division problem into simpler, more manageable steps. It involves finding partial quotients for each part of the dividend. These partial quotients are then added together to obtain the final quotient.

This approach is useful when dealing with large division problems since it makes division more understandable and less overwhelming for kids. The partial quotient method is also called the “chunking method” since it breaks down a large number into smaller parts.

What Is a Quotient?

The quotient is the number we obtain when dividing one number (dividend) by another (divisor). Note that the quotient is always smaller than the dividend.

Example: $8 \div 4 = 2$

Here, 8 is the dividend, and 4 is the divisor. 

The result of the division is 2.

Thus, 2 is the quotient.

Partial Quotient Definition

Partial quotient is a division method that breaks down a dividend into smaller parts, enabling easier subtraction of multiples of the divisor until the remainder is smaller than the divisor. 

Understanding Partial Quotients as a Division Strategy

The division operation is defined as the process of repeated subtraction. It is exactly the opposite of multiplication. In the standard form of division, the divisor is used to determine how many times it can be subtracted from the dividend.

Example: $20 \div 5$ 

$20 – 5 = 15$

$15 – 5 = 10$

$10 – 5 = 5$

$5 – 5 = 0$

5 is subtracted 4 times to get the remainder of 0.

$20 \div 5 = 4$

Here, we can easily identify that 

$5 \times 4 =$ Four groups of $5 = 5 + 5 + 5 + 5 = 20$

Thus, quotient $= 4$

In the partial quotient division, we break the dividend into smaller parts by subtracting multiples of the divisor until the remainder is 0 or less than the divisor. The multipliers (numbers used to multiply the divisor to find these multiples) are the partial quotients, which are then summed to find the final quotient.

Example: $285 \div 5$

Using repeated subtraction, we will have to subtract 5 multiple times to find the quotient. It would be tedious. Instead, we can use the partial quotients.  

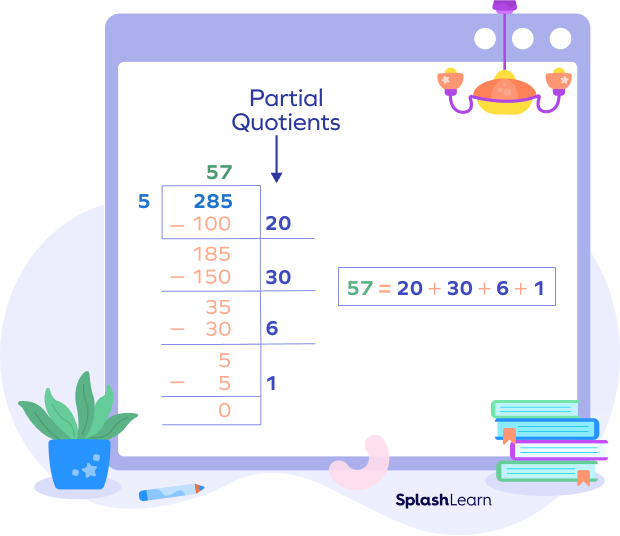
Thus, 5 can be subtracted 57 times from 285. To reach the final quotient of 57, we preferred chunking the division process into smaller steps. The outcome is the same, no matter how many steps you choose. The numbers with which the divisor is multiplied during this process are called the partial quotients.

Here’s how we can solve the same example using different partial quotients.

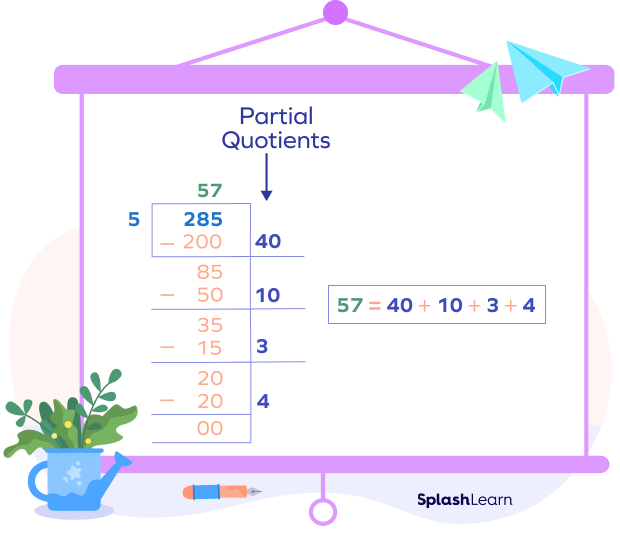
How to Divide Using the Partial Quotient Method

Let’s understand the steps to divide using the partial quotients with the help of an example.

• Identify the dividend and the divisor: Understand the division problem, which consists of a dividend (the number to be divided) and a divisor (the number you’re dividing by).

• Estimate Partial Quotients: Choose a multiple of the divisor that is as close as possible to the dividend without exceeding it. The best approach would be to write simple multiplication facts of the divisor (such as multiples of 10).

The multiplier of the divisor at every step of this division is the partial quotient. This multiple of the divisor should be as close as possible to the dividend, that is, less than or equal to the dividend.

• Subtract: Subtract the multiple from the dividend to find the remainder.

• Continue the process: If the remainder is not zero, repeat the process. Find another multiple of the divisor that can be subtracted from the remaining dividend to obtain the next partial quotient. Repeat this process until the remainder is 0 or less than the divisor.

• Combine Partial Quotients: Keep finding partial quotients and subtracting them until the remainder is zero or less than the divisor. Then, add all the partial quotients together to obtain the final quotient.

• Check your answer: Verify that your answer is correct by multiplying the divisor by the quotient and adding any remaining remainder. It should equal the original dividend.

Example 1: Divide 378 by 6 using partial quotients.

Dividend $= 378$

Divisor $= 6$

Example 2: Let’s consider an example where the remainder is not 0.

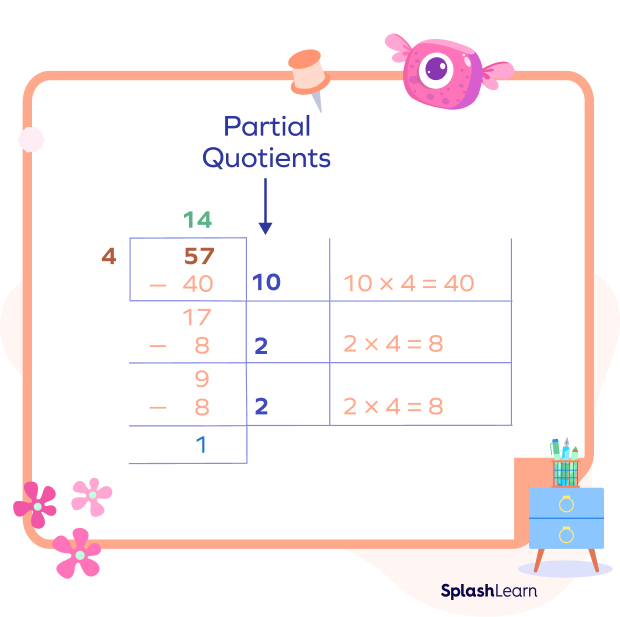
Adding the partial quotients, we get

$10 + 2 + 2 = 14$

We also have a remainder of 1. 

Thus, $57 \div 4 = 14$ R 1

We can also write this using mixed fractions as 

$57 \div 4 = 14 \frac{1}{4}$

How to Use Partial Quotients to Divide by One-Digit Numbers

The steps are the same. Let’s consider an example. Let’s divide 78 by 3.

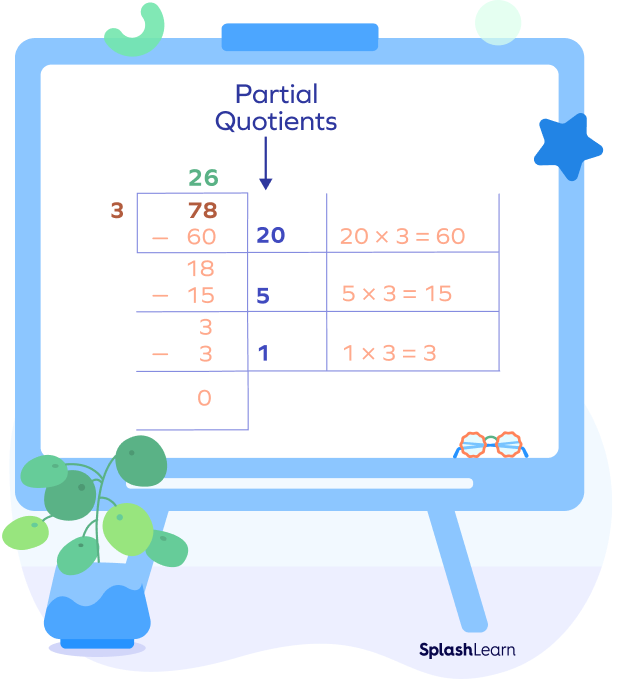
How to Use Partial Quotients to Divide by Two-Digit Numbers

The process discussed earlier stays the same regardless of the number of digits in the divisor.

Example: $1275 \div 15$

Partial Quotients Using Area Model

The area model division method visually represents division using rectangles, where the partial quotients and the divisor determine the length and width of these rectangles. Each partial quotient corresponds to the length of one rectangle. The combined area of these rectangles equals the dividend of the division equation.

Example: $275 \div 25$

Dividend $= 275$

Divisor $= 25$

We can choose as many rectangles as we choose the number of partial quotients. 

Suppose we choose two partial quotients, 10 and 1.

Division Step i) 

$25 \times 10 = 250$ 

$275 – 250 = 25$

Division Step ii) 

$25 \times 1 = 25$ 

$25 – 25 = 0$

Consider two rectangles, both having a width equal to the value of the divisor, 25.

Divisor $= 25 =$ Width of the rectangles

Length of one rectangle $= 25$ …partial quotient

Length of the other rectangle $= 1$ …partial quotient

Sum of partial quotients $= 10 + 1 = 11 =$ Length of the big rectangle

Sum of areas of two rectangles $= 250 + 25 = 275$ square units = Dividend

How to Divide Decimals Using Partial Quotients

Let’s understand how to divide decimals using partial quotients. The process is similar, but we must consider the decimal point at every step.

Example: $9.7 \div 4 = 2.425$

Facts about Partial Quotients

Conclusion

In this article, we learned about the partial quotient division method. We discussed how to divide numbers and decimals easily using partial quotients. Let’s solve a few examples for better comprehension.

Solved Examples on Partial Quotients

1. Solve 112 ÷ 4  using partial quotients. 

Solution:

Let’s use the partial quotients method.

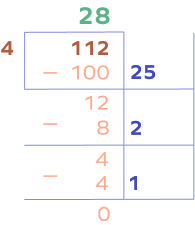
Quotient $= 25 + 2 + 1 = 28$

Thus, $112 \div 4 = 28$

2. Solve 108 ÷ 3 using partial quotients. 

Solution:

Let’s use the partial quotient method.

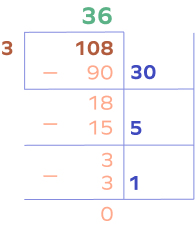
Final quotient $= 30 + 5 +  1 =  36$

Thus, $108 \div 3 = 36$

3. Find partial quotients and the final quotient.

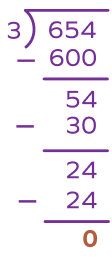
Solution:

Dividend $= 654$

Divisor $= 3$

1st partial quotient $= 200$ since $200 \times 3 = 600$

2nd partial quotient $= 10$ since $10 \times 3 = 30$

3rd partial quotient $= 8$ since $8 \times 3 = 24$

Final quotient = Sum of partial quotients $= 200 + 10 + 8 = 218$

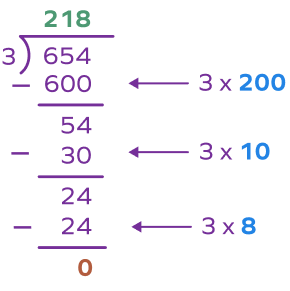
Practice Problems on Partial Quotients

Frequently Asked Questions about Partial Quotients