Factors and Multiples – Definition, Differences, Examples, FAQs

What Are Factors and Multiples?

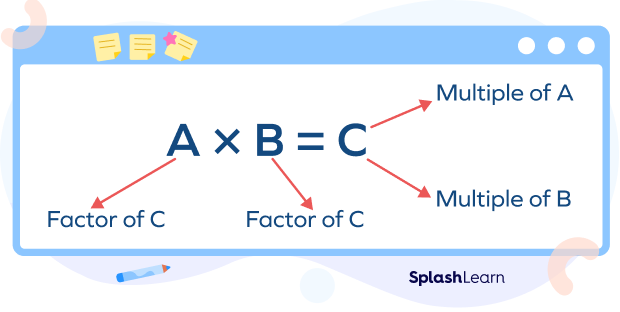
Factors and multiples are two interrelated concepts in mathematics. If $A \times B = C$, then A and B are factors of C, whereas C is a multiple of both A and B.

Consider an example to understand.

Example: $3 \times 7 = 21$

Here, 3 and 7 are factors of 21.

21 is the multiple of both 3 and 7.

What Are Factors?

A factor is a number that divides the given number exactly, without any remainder. When a number n is divisible by b, we can say that b is a factor of n.

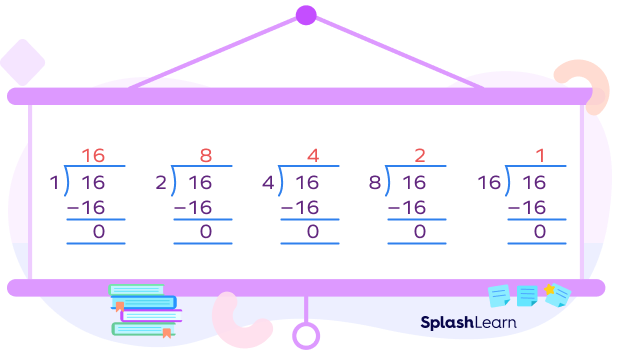
For example, the factors of 16 are 1, 2, 4, 8, and 16, because these numbers divide 16 exactly, without leaving any remainder.

Properties of Factors

• 1 is the smallest factor of any number.
• The number itself is the greatest factor of any number.
• A factor of a number is always less than or equal to the number.
• Factors of a number are finite.
• 0 cannot be a factor of any number.
• If B is a multiple of A, then A is a factor of B.

What Are Multiples?

A multiple of a number is the number obtained when the given number is multiplied with an integer. 

A multiple is a result of multiplying a number by an integer. Note that, when we study multiples of any number, we generally talk about positive multiples only (excluding 0 and negative multiples). Thus, we can say that a multiple is the number obtained by multiplying a given number by a positive integer. 

For example, the multiples of 5 are 5, 10, 15, 20,…, and so on, because these numbers can be obtained by multiplying 5 with the whole numbers 1, 2, 3, 4,…, and so on.

You can find the multiples of a number in the multiplication table (times table). Take a look!

$5 \times 1 = 5$

$5 \times 2 = 10$

$5 \times 3 = 15$

$5 \times 4 = 20$

$5 \times 5 = 25$

$5 \times 6 = 30$

$5 \times 7 = 35$

$5 \times 8 = 40$

$5 \times 9 = 45$

$5 \times 10 = 50$

Properties of Multiples

• Infinitely many multiples of any number.
• A multiple is always greater than or equal to the given number.
• Every number is a multiple of 1.
• If B is a multiple of A, then A is a factor of B.
• 0 is considered a multiple of every number.

Difference Between Factors and Multiples

Factors	Multiples
Factors are numbers that divide the given number without leaving a remainder.	Multiples are the numbers obtained as a product of a given number and integers.
A factor of a number is less than or equal to itself.	Multiples are always greater than or equal to the given number.
Factors are finite in number and include 1 and the number itself.	There are an infinite number of multiples for a given number.
1 is the smallest factor of any number.	Every number is a multiple of 1.
0 cannot be a factor of any number.	0 is a multiple of every number.
Example: Factors of 8 are 1, 2, 4, 8.	Example: Multiples of 8 are 8, 16, 24,…

How to Find Factors and Multiples

Let’s move ahead and learn the methods we can use to find factors and multiples of a number.

How can we find factors?

To find the factors of a given number, divide the number by each integer between 1 and the number itself. The integers that give us a remainder of 0 are factors of the number. 

For example, to find the factors of 6, divide 6 by numbers 1 to 6.

61	Remainder $= 0$
62	Remainder $= 0$
63	Remainder $= 0$
64	Remainder $= 0$
65	Remainder $= 1$
66	Remainder $= 0$

The factors of 6 are 1, 2, 3, and 6.

How to find multiples

To find the multiples of a given number, multiply the number by each positive integer.

For example, to find the multiples of 5, you would multiply 5 by 1, 2, 3, 4, and so on.

Multiples of $5 = 5,\; 10,\; 15,\; 20,\; 25$, …

Multiples of $9 = 9\;, 18\;, 27\;, 36\;, 45$, …

Least Common Multiple (LCM)

LCM of two numbers is the smallest positive integer that is a multiple of both the numbers. It is the smallest number among the common multiples of the given two numbers.

Let’s find the LCM of 4 and 6. 

Multiples of 4	4	8	12	16	20	24	…
Multiples of 6	6	12	18	24	30	36	…

Common multiples $= 12,\; 24,\; 36$, …

Least common multiple $= 12$

LCM (4, 6) $= 12$

Greatest Common Factor (GCF)

It is the largest positive integer that divides the given two integers without leaving any remainder. In other words, it is the largest number that is a factor of all the given integers.

Let’s find the GCD of 12 and 18.

Factors of 12	1	2	3	6	12	–
Factors of 18	1	2	3	6	9	18

The largest number that appears in both lists is 6. 

GCF of 12 and 18 is 6.

Facts about Factors and Multiples

Conclusion

In this article, we have learned about factors and multiples, the definitions, how to find factors and multiples, and also the properties of multiples and factors of a number. We have also learned some interesting facts about factors and multiples. Let’s now look at some solved examples and practice problems to understand the concept better.

Solved Examples on Factors and Multiples

1. Find the factors of 30.

Solution: 

The factors of 30 are the integers that divide 30 without leaving any remainder.

$30 \div 1 = 30 \text{and remainder} = 0$

$30 \div 2 = 15 \text{and remainder} = 0$

$30 \div 3 = 10 \text{and remainder} = 0$

$30 \div 5 = 6 \text{and remainder} = 0$

$30 \div 6 = 5 \text{and remainder} = 0$

30 \div 10 = 3 \text{and remainder} = 0$

$30 \div 15 = 2 \text{and remainder} = 0$

$30 \div 30 = 1 \text{and remainder} = 0$

Thus, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.

2. Find the multiples of 7 that are less than or equal to 56.

Solution: 

We can write the multiples of 7 as,

$7 \times 1 = 7$

$7 \times 2 = 14$

$7 \times 3 = 21$

$7 \times 4 = 28$

$7 \times 5 = 35$

$7 \times 6 = 42$

$7 \times 7 = 49$

$7 \times 8 = 56$

$7 \times 9 = 63$

Hence, the multiples of 7 that are less than or equal to 56 are 7, 14, 21, 28, 35, 42, 49, and 56.

3. Find the least common multiple (LCM) of 8 and 12.

Solution: 

Multiples of 8: 8, 16, 24, 32, 40, 48…

Multiples of 12: 12, 24, 36, 48…

Common multiples: 24, 48…

LCM of 8 and 12 is the smallest number that is a multiple of both 8 and 12, which is 24.

4. Find the greatest common factor (GCF) of 18 and 48.

Solution: 

Factors of 18 are 1, 2, 3, 6, 9, and 18. 

Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. 

Hence, the GCF of 18 and 48 is the greatest number that is a factor of both 18 and 24, which is 6.

5. If 20 and 35 are both factors of a number n, what is the smallest possible value of n?

Solution: 

The smallest possible value of n is the least common multiple (LCM) of 20 and 35.

The multiples of 20 are 20, 40, 60, 80, 100, 120, 140, 160, 180… and so on.

And 

The multiples of 35 are 20, 40, 60, 80, 100, 120, 140, 160, 180… and so on.

LCM of 20 and $35 = 140$.

Hence, the smallest possible value of n is 140.

Practice Problems on Factors and Multiples

Frequently Asked Questions about Factors and Multiples