Dividing a Fraction by a Whole Number – Examples, FAQs

Dividing Fractions with Whole Numbers: Introduction

Suppose you have to divide a half pizza among 6 friends. To find the share of each friend requires you to divide a fraction $\frac{1}{2}$ by a whole number, 6. The following image shows two half parts of a whole pizza. Each half is further divided into 6 equal parts. So, if you pick any small slice, it represents $\frac{1}{12}$ fraction of whole. 

Dividing a fraction by a whole number requires an understanding of some basic concepts like fractions, mixed fractions, reciprocals of fractions, and whole numbers. 

• Whole numbers include natural numbers and 0.

Whole numbers: 0, 1, 2, 3, 4 . . . 

• A fraction is a part of a whole. For instance, one whole circle divided into two equal parts gives us two halves. If a circle is divided into 4 equal parts, each part equals $\frac{1}{4}$ or a quarter.

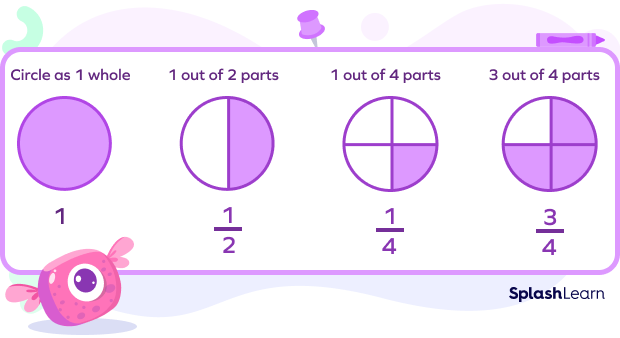
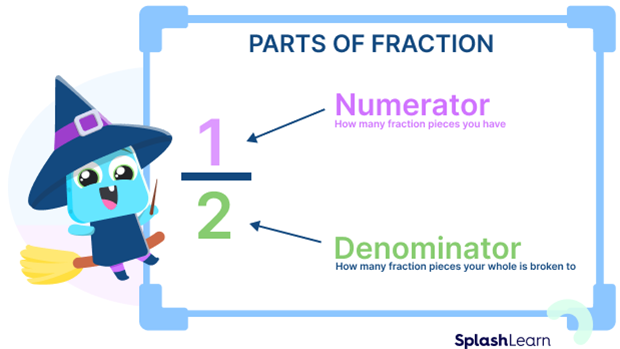
In the fraction $\frac{1}{2}$, 1 is the numerator, and 2 is the denominator.

Reciprocal of Fractions

The reciprocal of a fraction is obtained by interchanging the numerator and denominator with each other.

For example: The reciprocal of the fraction $\frac{5}{7}$ will be $\frac{7}{5}$.

We can also find the reciprocal of a whole number.

For example: The reciprocal of the whole number 2 will be $\frac{1}{2}$.

For more examples of reciprocals, look at the image below:

A fraction’s product with its reciprocal is always equal to one. 

For example, $\frac{3}{2} \times \frac{2}{3} = 1$.

How to Divide a Fraction by a Whole Number?

Let’s understand the concept of dividing a fraction by a whole number with an example.

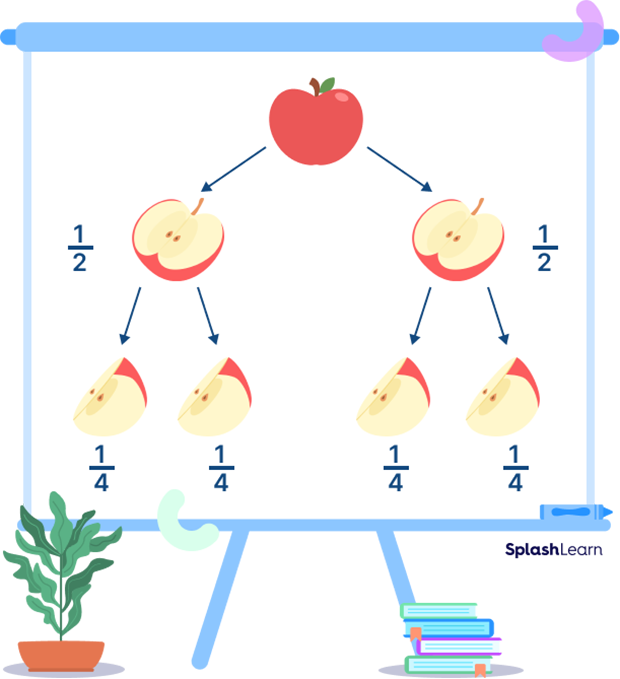
Suppose an apple is to be divided between two friends equally. It will be cut into two pieces, and each friend will get half an apple.

Now suppose two more friends join. In this case, each half will be cut into two equal parts, which is equivalent to dividing the fraction $\frac{1}{2}$ by 2. So, each friend will now get one-fourth or $\frac{1}{4}$ of the whole apple. 

$\frac{1}{2} \div 2 = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$

So, dividing the fraction by 2 is equivalent to multiplying the fraction by the reciprocal of 2, which is $\frac{1}{2}$.

Three steps are usually used in dividing a fraction by a whole number.

• Step 1: Write the problem in an equation format.
• Step 2: Change the division sign with multiplication and replace the divisor by its reciprocal.
• Step 3: Multiply the numerator with the numerator and the denominator with the denominator to reach the required answer. 

Let’s discuss two more examples.

Example 1: Divide a/b by u.

Step 1: $\frac{a}{b} \div u$  

Step 2: $\frac{a}{b} \times \frac{1}{u}$

Step 3: $\frac{a \times 1}{b \times u}= \frac{a}{bu}$

Example 2: Divide $\frac{3}{5}$ by 6.

Step 1: $\frac{3}{5} \div 6$.

Step 2: $\frac{3}{5} \times \frac{1}{6}$.

Step 3: $\frac{3 \times 1}{5 \times 6} = \frac{3}{30} = \frac{1}{10}$

How to Divide a Mixed Fraction by a Whole Number?

Before we learn how to divide a mixed fraction by a whole number, let’s do a quick revision of some important concepts.

Mixed Fractions 

A mixed fraction is a fraction consisting of a whole number and a fraction. 

For example, 7 is a whole number, and $1/3$ is a fraction, making $7\frac{1}{3}$ a mixed fraction.

It can also be written as $\frac{22}{3}$ (improper fraction).

Mixed Fractions and Improper Fractions 

A fraction where the numerator is greater than the denominator is called an improper fraction. Mixed fractions and improper fractions basically represent the same thing. We just write them in different formats. 

For example: To convert the mixed fraction 347 into an improper fraction:

                        $3\frac{4}{7} =\frac{(7 \times 3) + 4}{7}= \frac{25}{7}$

Now, let’s understand the division of a mixed fraction by a whole number with the help of an example.

Divide  $4\frac{5}{3}$ by 7.

First, we write the mixed fraction  $4\frac{5}{3}$ as an improper fraction, i.e., $\frac{17}{13}$. 

Now, we follow the same three steps as discussed above.

Write the problem as $4\frac{5}{3} \div \frac{7}{1}$.

$= \frac{17}{13} \times \frac{1}{7}$

$= \frac{17 \times 1}{13 \times 7}$

$= \frac{17}{91}$

How to Divide Whole Numbers by a Fraction?

Since you have become familiar with dividing a fraction by a whole number, let’s now understand its reverse case.

Division of a whole number by a fraction requires the following steps:

1. Write the whole number as an improper fraction.
2. Follow the three steps of dividing a fraction by the whole number.

Example: Divide 12 by $\frac{4}{5}$.

First, we convert 12 into an improper fraction, i.e., $\frac{12}{1}$.

Then, we write the problem $\frac{12}{1} \div \frac{4}{5}$.

$= \frac{12}{1} \times \frac{5}{4}$

$= \frac{12 \times 5}{1 \times 4}$

$= \frac{60}{4}$

$ = 15$

Fun Fact!

• Division of a whole number by a fraction results in either a whole number or an improper fraction.

Conclusion

Dividing a fraction by a whole number involves using concepts related to fractions and whole numbers. So, having a basic understanding of these is crucial as it helps you comprehend and follow the three steps involved in the division of fractions.

The division of a whole number by a fraction follows the same three steps with a slight variation of converting the whole number into an improper fraction. 

All in all, knowing the division of fractions is essential as it lays the foundation for understanding complex fractional problems in higher classes.

Solved Examples on Dividing Fractions with Whole Numbers

1. Change the mixed fraction $7\frac{2}{3}$ into an improper fraction.

Solution: First, we take the product of the whole number 7 with the denominator 3 and add the numerator 2 to it. The denominator 3 stays the same.

$7\frac{2}{3} = \frac{(7 \times 3) + 2}{3}$

         $= \frac{23}{3}$

Then, we will get the numerator as 23. The denominator will stay the same.

Thus, $\frac{23}{3}$ will be the resulting improper fraction.

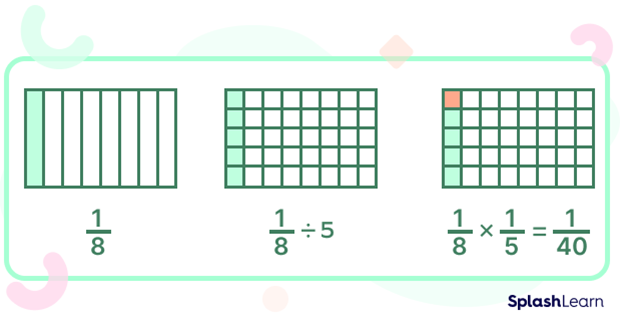
2. Divide $\frac{5}{8}$ by 12.

Solution: For dividing the fraction (58) with the whole number (12), we write:

$\frac{5}{8} \div 12$

$= \frac{5}{8} \times \frac{1}{12}$

$= \frac{5}{96}$

3. Divide $5\frac{4}{9}$ by 7.

Solution: First, we convert the mixed fraction into an improper fraction, i.e., $5\frac{4}{9} = \frac{49}{9}$

Then, we write the problem as $49/9 \div 7$

$= \frac{49}{9} \times \frac{1}{7}$

$= \frac{49 \times 1}{9 \times 7})$

$= \frac{49}{63}$

$= \frac{7}{9}$

4. Divide 24 by $\frac{3}{2}$.

Solution: First, we change the number into an improper fraction, i.e., $\frac{24}{1}$.

Then, we write the problem as $\frac{24}{1} \div \frac{3}{2}$.

$= \frac{24}{1} \times \frac{2}{3}$

$= \frac{24 \times 2}{1 \times 3}$

$= \frac{48}{3}$

$= 16$

5. Ben has to divide $\frac{5}{4}$ by 25 as a part of his assignment. Help him out by dividing the fraction by a whole number.

Solution: For dividing the fraction $\frac{5}{4}$ by the whole number 25, we need to write the problem as:

$\frac{5}{4} \div 25$

$= \frac{5}{4} \times \frac{1}{25}$

$= \frac{5 \times 1} {4 \times 25}$

$= \frac{5}{100}$

Practice Problems on Dividing Fractions with Whole Numbers

Frequently Asked Questions on Dividing Fractions with Whole Numbers