Perimeter of Rectangle
The perimeter of a two-dimensional shape is the total length of the outline. To find the perimeter of a rectangle, we add the lengths of all four sides. Since opposite sides of a rectangle are always equal, we need to find the dimensions of length and width to find the perimeter of a rectangle. We can write the perimeter of the rectangle as twice the sum of its length and width. The perimeter is a linear measure and has units as meters, centimeters, inches, feet, etc.
Recommended Games
Formula for the Perimeter of a Rectangle
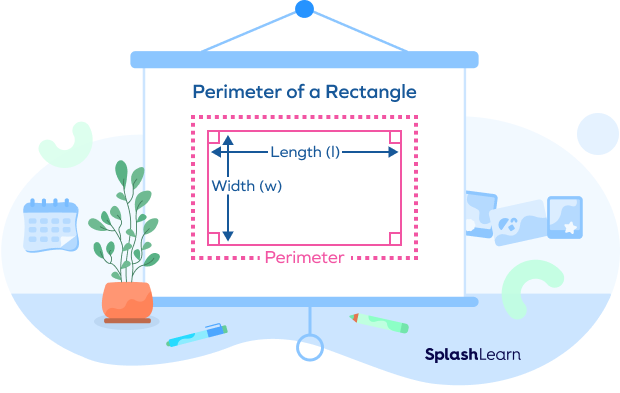
The letter ‘P’ denotes the perimeter of a rectangle. Let l denote the length and w denote the width of the rectangle. The perimeter (P) of a rectangle is the total length of all the sides of the rectangle. Since the opposite sides of a rectangle are equal, a rectangle has two equal lengths and two equal widths.
The formula for the perimeter of a rectangle is given below:
Perimeter = length + length + width + width
P = l + l + w + w
Or, P = 2 (l + w)
Hence, the formula for the perimeter of a rectangle, P = 2 × (length + width) = 2 × (sum of adjacent sides)
Recommended Worksheets
Real-World Applications
- To find out the distance covered by walking around a rectangular park.
- To measure the length of barbed wire required to create a fence around a rectangular plot of land.
- To draw a border with limestone around a rectangular ground and determine how much limestone would be required to mark the ground’s total periphery.
Solved Examples On Perimeter of Rectangle
- The length of a rectangle is 25 cm and the width is 4 cm. What is the perimeter of this rectangle?
Solution:
Length of the rectangle, l = 25 cm
Width of the rectangle, w = 4 cm
Perimeter of the rectangle, P = 2 (l + w) = 2 (25 + 4) = 58
The perimeter of the given rectangle is 58 cm.
- The length of a rectangular yard is 10 m more than the width. If the yard’s length is 25 m, find the perimeter of this rectangular yard?
Solution:
The length of the rectangular yard is 10 m more than the width. Since the length of the yard is 25 m, the width of this rectangular yard is 25 m – 10 m or 15 m.
Length of the yard, l = 25 m
Width of the yard, w = 15 m
Perimeter, P = 2 (l + w) = 2 (25 + 15) = 2 (40) = 80
The perimeter of the given rectangle is 80 m.
- The perimeter of a rectangle is 100 cm. The length of this rectangle is 35 cm. Calculate the width of the rectangle.
Solution:
Using the formula P = 2 (l + w), we can say that 2 (35 + w) = 100
Or, 35 + w = 1002 = 50
Therefore w = 50 – 35 = 15
The width of the given rectangle is 15 cm.
Practice Problems On Perimeter of Rectangle
Perimeter Of A Rectangle
The perimeter of a rectangle is 150 cm, and the width is 20 cm. What is the length of this rectangle?
150 = 2 (l + 20). Hence, l + 20 = 150 ÷ 2 = 75, or l = 75 - 20 = 55 cm.
The length and width of a rectangle are 35 cm and 25 cm, respectively. What is the perimeter of this rectangle?
P = 2(35+25) = 2(60) = 120 cm
The length of a rectangle is twice its width. If the width of a rectangle is 45 cm, calculate the perimeter of the rectangle.
Length = 2(width) = 2(45) = 90 cm. So, P = 2(90 + 45) = 2(135) = 270 cm.
The perimeter of a rectangle is 250 cm. The length of the rectangle is 1/5th of the perimeter. What is the width of the rectangle?
Length = ⅕ (250) = 50 cm. Now, P = 2 (50 + w) = 250. So, w = $\frac{250}{2}$ – 50 = 75 cm
Frequently Asked Questions On Perimeter of Rectangle
What is the difference between the perimeter and area of a rectangle?
The perimeter measures the length of the boundary of the rectangle. It is given by the sum of all sides of the rectangle and expressed in linear units. Area, on the other hand, measures the space within the rectangle. It is the product of the length and width of the rectangle and is expressed in square units.
Which unit of measurement is used to measure the perimeter of a rectangle?
Since the perimeter of a rectangle is the total distance covered by its boundaries or the sides, the unit of the perimeter (as distance) can be centimeters, meters, feet, yards, etc.
Can rectangles with the same perimeters have different sides and areas?
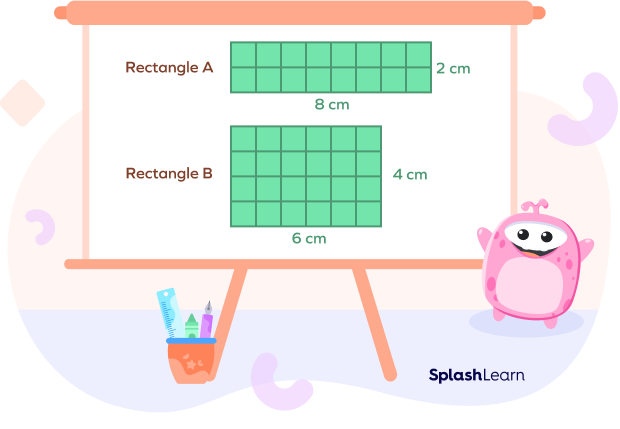
Yes. The perimeter of Rectangle A is 20 cm. The perimeter of Rectangle B is 20 cm. As the sides differ, so do their areas. The area of Rectangle A is 16 cm2, while the area of Rectangle B is 24 cm2.
How can you find the length of a rectangle with the given width and perimeter?
Perimeter of Rectangle = 2 (Length + Width). Rearranging the terms in this formula, we get, Length = $\frac{Perimeter}{2}$ – Width. So, to find the length of a rectangle, subtract the width from half of the perimeter.



























