Area of Rectangle Formula – Definition with Examples

Area of a Rectangle Formula

A rectangle is a 2-dimensional shape/polygon with four sides, four vertices, and four right angles. The two opposite sides in the rectangle are equal and parallel to each other. What is the area of a rectangle? It is the space covered by the shape or the space within the perimeter of the rectangle. Alternatively, the space within the perimeter of the rectangle is the area of a rectangle.

In geometry, the concept of area in a two-dimensional or three-dimensional figure helps us find the amount of space occupied by them. For example, for the given rectangle, the amount of color required to fill the rectangle can be found by determining its area.

Some examples of rectangular figures are agricultural fields, parks, tiles, daily life objects such as pans, glass, table, serving tray, etc.

The upcoming section discusses the methods to understand why the area of a rectangle is the product of its two sides as well as the units of measurement. 

How to Calculate the Area of a Rectangle?

To derive the area of a rectangle, we use the unit squares. How to find the area of a rectangle using unit squares?

We can find the area of any two-dimensional shape by dividing that shape into smaller unit squares. Since each unit square occupies one square unit space, the total number of unit squares in the shape gives its area. The area of a shape is measured in square units. So, the unit of area of a rectangle is ‘square units’. Let’s understand how to find the area of a rectangle using unit squares.

Example 1: Divide the rectangle ABCD into unit squares, as shown. The area of a rectangle ABCD is the total number of unit squares contained within it.

Thus, the total area of the rectangle ABCD is 48 sq. inch. 

Also, using this approach, we find that the area of a rectangle is always the product of its two sides. Here, the length of AB is 8 inches and the length of BC is 6 inches. The area of ABCD is the product of 6 and 8, which is equal to 48. 

Example 2: Consider a rectangle of length 6 in. and width 3 in. It can be filled with 3 rows and 6 columns of unit squares.

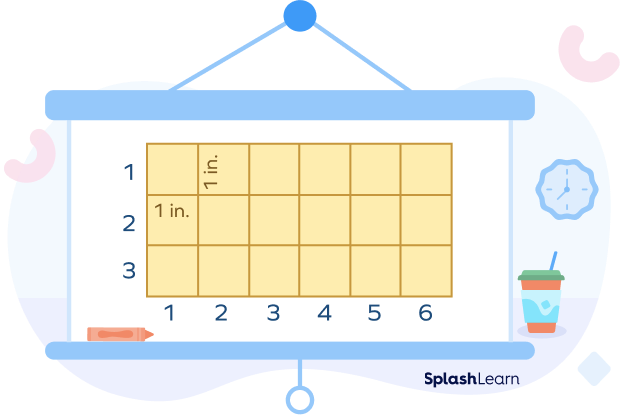
Each of these squares has an area of 1 square inch, and in the rectangle, there are 18 such squares. So, the area of the rectangle is 18 square inches. 

The unit of area of a rectangle is “square units” (square inches, square feets, etc) as the lengths are multiplied together, so are the units.

The formula for finding the area of a rectangle

Area of a rectangle $= \text{length} \text{(l)} \times \text{width} \text{(w)}$

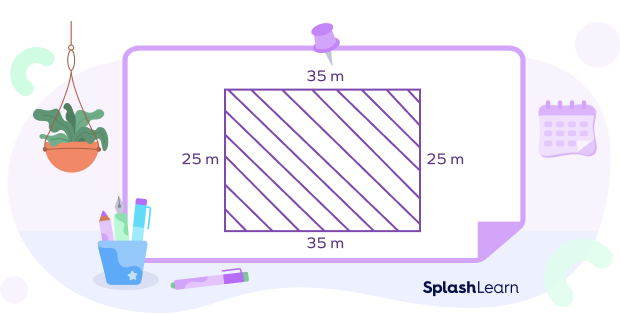
For example, if the length of a rectangle is 35 m and width is 25 m, then the area is $35 \times 25 = 875$ square meters.

Alternatively, the formula to calculate the area of a rectangle is derived by dividing the shape into two equal size right triangles. For example, in the given rectangle ABCD, a diagonal from the vertex A is drawn to C.

The diagonal AC divides the rectangle into two equal right angle triangles. 

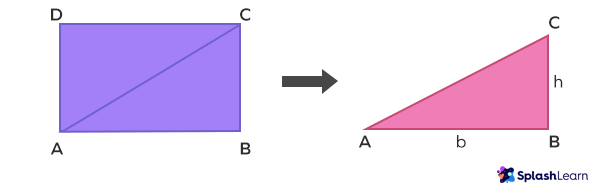
Thus, the area of ABCD will be:

      $⇒ \text{Area} (▭\text{ABCD}) = \text{Area} (\Delta \text{ABC}) + \text{Area} (\Delta \text{ADC})$

     $⇒ \text{Area} (▭\text{ABCD}) = 2 \times \text{Area} (\Delta \text{ABC})$

     Here,  Area $(\Delta \text{ABC}) = \frac{1}{2} \times \text{base} \times \text{height}$

      $⇒ \text{Area} (▭\text{ABCD}) = 2 \times (\frac{1}{2} \times \text{b} \times \text{h})$

      $⇒ \text{Area} (▭\text{ABCD}) = \text{b} \times \text{h}$

Applications

The early transcripts of Babylonian culture signify the use of geometric shapes with lengths, angles, and areas for construction and astronomy. The knowledge of stone cutting in basic shapes such as triangles, squares, and rectangles along with principles pertaining area and perimeter helped Egyptians to build giant structures like pyramids. In modern mathematics, these concepts are useful in map designing, land surveying, object modeling, and others. 

Fun Facts

1. Both the diagonals of a rectangle are of equal length.

2. A circle can contain a rectangle with all its vertex touching the circumference; it is called a cyclic rectangle.

3. The square is a special type of rectangle whose length and width are the same. Hence, the area of a square is given by multiplying the length of each side by itself.

Solved Examples

1. Calculate the area of a rectangle with a width of 5 cm and a length of 20 cm.

Solution:

Given,

Width $\text{(w)} = 5 \text{cm}, \text{Length (l)} = 20$ cm

Area $= \text{l} \times \text{w} = 20 \times 5  = 100$

Hence, area $= 100 \text{cm}^2$

2. What is the area of a rectangular table in $\text{m}^2$with a length of 130 cm and a width of 110 cm?

Solution:

Length of the table $= \text{l} = 130 \text{cm}$ $\text{or} 1.3$ m

width of the table $= \text{w} = 110 \text{cm}$ $\text{or} 1.1$ m

Area of the rectangular table $= \text{l} \times \text{w}  = 1.3 \text{m} \times 1.1 \text{m} = 1.43 \text{m}^2$

3. A rectangular window measures 25 feet in length. It has a $100 \text{feet}^2$ area. Determine the width of the window.

Solution:

Area of the window $= 100 \text{feet}^2$

Length of the window $= \text{l} = 25$ feet

Area $= \text{l} \times \text{w}$

$100 = 25 \times \text{w}$

Thus, width of the window $= \frac{100}{25}  = 4$ feet

4. A rectangular room has a length of 12 feet and a width of 14 feet. How much carpet is required to cover the entire room?

The area of the carpet is equal to the area of the room.

 We can find the area of the room by multiplying its length by width. 

Area of carpet $= \text{length} \times \text{width}$

Area of carpet $= 12 \times 14 = 168$ square feet. 

Therefore, to cover the room, 168 square feet of carpet is required.

Practice Problems