What Is a Hemisphere Shape in Geometry?
A hemisphere is formed when a plane cuts a sphere in half. When a sphere is divided into two equal halves, each half is then called a hemisphere.
A sphere is a 3D round shaped solid. Each point on its surface is equidistant from the center.
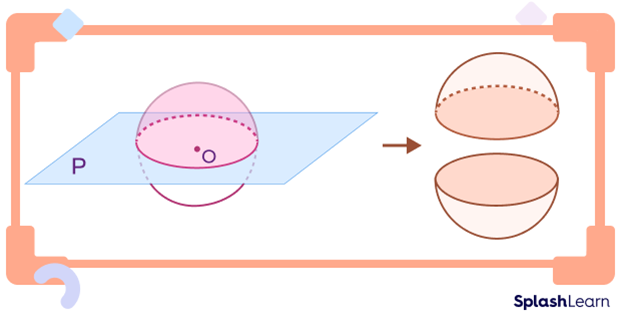
So, what does a hemisphere look like? Take a look at the image shown below!
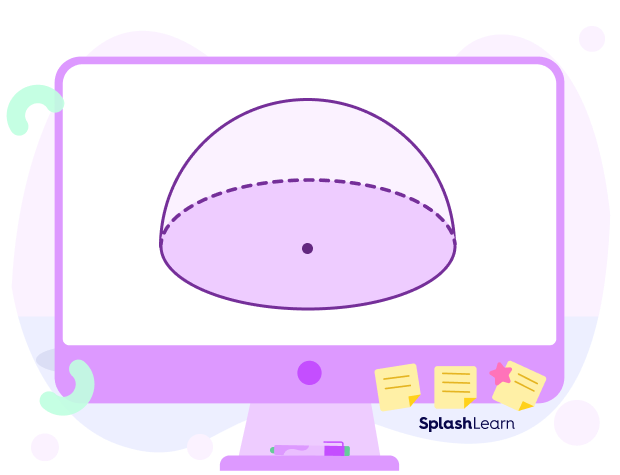
It has a flat circular base and a curved surface. Note that the radius of the hemisphere is equal to the radius of the sphere it is cut from.
In everyday life, we come across a variety of hemisphere-shaped objects. For instance, if we cut a perfectly round lemon or an orange in identical halves, we get two hemispheres.

Recommended Games
Hemisphere: Definition
A hemisphere is a geometric shape that is exactly half of a sphere. The prefix “hemi” means “half.”
Recommended Worksheets
Properties of a Hemisphere
- The radius of the hemisphere is equal to the radius of the sphere.
- A hemisphere has a flat circular base and a curved surface.
- A hemisphere has no edges and no vertices, just like a sphere.
- A hemisphere is not a polyhedron since it has a circular base and one curved surface.
- A line segment that meets the two opposite points on the base of a hemisphere and passes through its center is said to have that object’s diameter.
Volume of a Hemisphere
A hemisphere’s volume is defined as the 3D space occupied by it, it is expressed in cubic units.
The volume of sphere is calculated using the formula $V = \frac{4}{3} \pi r^{3}$
We know the hemisphere is simply half of the sphere. The volume of the hemisphere is also half the volume of the sphere.
Hemisphere Volume $= \frac{2}{3} \pi r^{3}$
where
r is the hemisphere’s radius,
$\pi = 3.142$ or $227.
Total Surface Area of the Hemisphere
A hemisphere’s total surface area is the sum of its curved surface area and area of the circular base.
Curved surface area $= 2\pi r^{2}$
Area of the circular base $ = \pi r^{2}$
Total Surface Area $= 2 \pi r^{2} + \pi r^{2} = 3 \pi r^{2}$
Where r is the hemisphere’s radius and π is a constant that is assumed to be 3.142 or $\frac{22}{7}$.
Curved Surface Area of the Hemisphere
The area of a curved surface of the hemisphere is given by
Hemisphere Curved Surface Area $= 2 \pi r^{2}$
where r is the hemisphere’s radius and π is the constant, given as 3.142 or $\frac{22}{7}$.
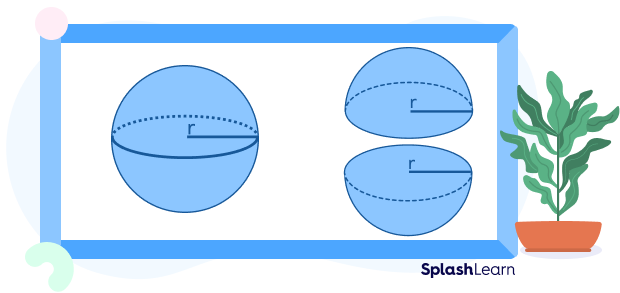
Difference between Hemisphere and Sphere
How is a hemisphere different from a sphere? Let’s make a chart and discuss!
| Hemisphere | Sphere |
|---|---|
| It is a 3D figure that is created when a plane cuts a sphere in two halves. | A sphere is a round solid shape that has no edges, or vertices. Each point on its surface is equidistant from the center. |
| It has a curved surface and a flat circular base. | Sphere is completely curved and has no flat surface. |
| Volume of a hemisphere $= \frac{2}{3}\pi r^{3}$ | Volume of a sphere $= \frac{4}{3} \pi r^{3}$ |
| Total surface area of a hemisphere $= 3 \pi r^{2}$ | Total surface area of a sphere $= 4 \pi r^{2}$ |
Hemisphere Shapes Around Us
There are many objects in daily life that have a hemispherical shape. Take a look at examples of hemispheres in real life.

Facts about Hemisphere
- A hollow hemisphere has two diameters for its circular base:
Outer radius: for outside circular base (rigid part)
Inner radius: for inside circular base (hollow part)
Therefore, the area of the hollow hemisphere is equal to the difference between the area of the external hemisphere and the area of the internal hemisphere. - Hollow Hemisphere Surface Area $= 2 \pi (r_{1}^{2} + r_{2}^{2}) + (r_{1}^{2}\;-\;r_{2}^{2})$.
where $r_{1}$ and $r_{2}$ are the hollow hemisphere’s outer and inner radii respectively and π is a constant that is assumed to be 3.142 or $\frac{22}{7}$.
Conclusion
A hemisphere is a 3D geometric object that is half of a sphere. In this article, we learned about the hemisphere shape in detail along with its properties and important formulas. Let’s solve a few examples and practice problems for better understanding!
Solved Examples on Hemisphere Shape
1. Determine the curved surface area of a hemisphere with radius 35 inches.
Solution:
We know that the curved surface area of a hemisphere is given by 2πr2.
Here, $r = 35$ in
$CSA = 2\pi r^{2}$
$CSA = 2\times \frac{22}{7} \times 35 \times 35$
$CSA = 7700\; inches^{2}$
Thus, a hemisphere with a radius of 35 inches has a curved surface area of 7700 inches2.
2. What is the volume of a hemisphere with an 11.2 inch radius?
Solution:
We know that the volume of a hemisphere $= \frac{2}{3} \pi r^{3}$.
Here, radius $= r = 11.2$ in
Volume of hemisphere $= \frac{2}{3} \pi r^{3} = \frac{2}{3} \times (3.14) (11.2)^{3} = 2940.98\; inches^{3}$.
Thus, the volume of the hemisphere with radius 11.2 inches is $2940.98\; inches^{3}$.
3. Given a hemispherical bowl with a radius of 10 cm, how much water can it hold?
Solution:
We know that the volume of a hemisphere is given by $\frac{2}{3} \pi r^{3}$.
$r = 10$ cm
Volume $= \frac{2}{3} \pi r^{3} = \frac{2}{3} \times (3.14)(10)^{3} = 2093.3$ cubic cm.
Thus, the volume of a hemisphere with a radius of 5 inches is approximately 2093 cubic cm.
4. Calculate the volume of a hemisphere with a 7 feet radius.
Solution:
Radius of the hemisphere$ = 7$ feet.
Therefore, the volume $= \frac{2}{3} \times \frac{22}{7} \times 7^{3} = \frac{2156}{3} = 718.66\; feet^{3}$
The volume of a hemisphere with a radius of 7 feet is therefore 718.66 cubic feet.
5. Calculate the TSA of the hemisphere with a radius of 10 cm.
Solution:
Total surface area of hemisphere $= 3\pi r^{2}$.
$r = 10$ cm
TSA of the given hemisphere $= 3\pi r^{2} = 3 \times \frac{22}{7} \times 10^{2} = \frac{6600}{7} = 942.85\; cm^{2}$
Practice Problems on Hemisphere Shape
Hemisphere Shape - Definition, Formula, Examples, Facts, FAQs
Hemisphere shape is the ______ of the sphere.
Hemisphere shape is half of the sphere.
Which of the following is NOT true about the hemisphere shape?
A polyhedron is a 3D shape made from polygons. A hemisphere is not a polygon since it has a curved surface and a circular base.
Calculate the radius of the hemisphere whose total surface area is 462 square units.
Total surface area of hemisphere $= 3\pi r^{2}$
$3\pi r^{2} = 462$
$\pi r^{2} = \frac{462}{3}$
$r^{2} = 49$
$r = 7$ units
Frequently Asked Questions on Hemisphere Shape
What distinguishes a hemisphere’s total surface from its curved surface area?
The curved surface area only includes the area of the curved region of the hemisphere. In contrast, the total surface area includes both the curved surface and the hemisphere’s base radius.
What number of faces does a hemisphere have?
A hemisphere has a circular flat base and one curved surface. A sphere only has one curved surface, whereas this object has several.
What is the ratio of the volumes of a sphere and a hemisphere if their radii are the same?
When the radii of a sphere and a hemisphere coincide, their volume ratio is 2:1.




































