Convert Hexadecimal To Binary – Definition, Table, Examples, FAQs

What Is the Hexadecimal to Binary Conversion?

Hexadecimal to binary conversion refers to finding the binary equivalent of a hexadecimal number. It is a conversion from base-16 number system to base-2 number system.

We know that the decimal number system with base = 10 is the most commonly used number system. Let’s get to know about the hexadecimal and binary number systems.

What is a Hexadecimal Number System?

The base of a hexadecimal system is 16. It used 16 symbols given by 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F to represent all the numbers. To represent the numbers 0-9, we simply use the same digits. To represent 10-15, we use the letters A-F.

The place values in the hexadecimal number system are expressed in terms of powers of 16.

What is a binary decimal system?

The base of a binary system is 2. The binary numbering system uses two digits, 0 and 1, to represent all the numbers. Binary digits 0 and 1 are also called bits. 

The place values in the binary number system are expressed in terms of powers of 2.

Hexadecimal to Binary Conversion Table

Here’s the hexadecimal to binary chart for quick conversions.

Decimal	Hexadecimal	Binary
0	0	00000000
1	1	00000001
2	2	00000010
3	3	00000011
4	4	00000100
5	5	00000101
6	6	00000110
7	7	00000111
8	8	00001000
9	9	00001001
10	A	00001010
11	B	00001011
12	C	00001100
13	D	00001101
14	E	00001110
15	F	00001111

How to Convert from Hexadecimal to Binary

There are different ways to convert a binary number into a hexadecimal number. Either we can convert using direct methods or indirect methods. 

Method 1: Hexadecimal to decimal followed by decimal to binary

Method 2: Hexadecimal to binary direct conversion

Method 1: Indirect Method

First, we convert a binary into the decimal system, and then we convert it to a hexadecimal number.

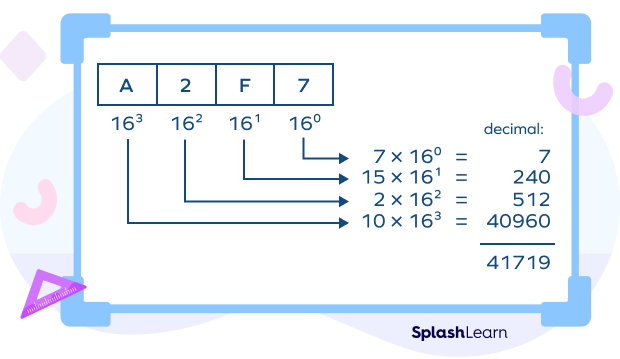
• Hexadecimal to Decimal: To convert from hexadecimal to decimal, multiply each digit by its respective place value, and finally add the products.

• Decimal to Binary: To convert from decimal to binary, divide the decimal number by 2 repeatedly, until the quotient is 0.

Example 1: (A2F7)₁₆

Example 2: Convert from hexadecimal to Binary: (6A)₁₆ 

Hex to decimal: Here, A = 10

$(6A)_{16} = 6 \times 16^{1} + 10 \times 16^{0}$

$(6A)_{16} = 96 + 10$

$(6A)_{16} = 106_{10}$

Decimal to binary:

Thus, (6A)₁₆ = 106₁₀ = (1101010)₂

Method 2: Direct Method: Hexadecimal to Binary Using Grouping and Conversion Table

There are only 16 digits from 0 to 7 and A to F in the hexadecimal number system, so we can represent any digit of the hexadecimal number system using only 4 bits as follows below.

Step 1: Divide the given hexadecimal number into individual digits.

Step 2: Assign binary equivalents to each hexadecimal digit. It’s important to keep track of leading zeros when converting hexadecimal to binary to maintain the correct number of digits.

Hexa	0	1	2	3	4	5	6	7
Binary	0000	0001	0010	0011	0100	0101	0110	0111

Hexa	8	9	A	B	C	D	E	F
Binary	1000	1001	1010	1011	1100	1101	1110	1111

Step 3: Replace each hexadecimal digit with its binary equivalent using the conversion table.

Example: Let’s convert the hexadecimal number “2A” to binary:

“2” in hexadecimal is equivalent to “0010” in binary.

“A” in hexadecimal is equivalent to “1010” in binary.

Therefore, “2A” in hexadecimal is equivalent to “00101010” in binary.

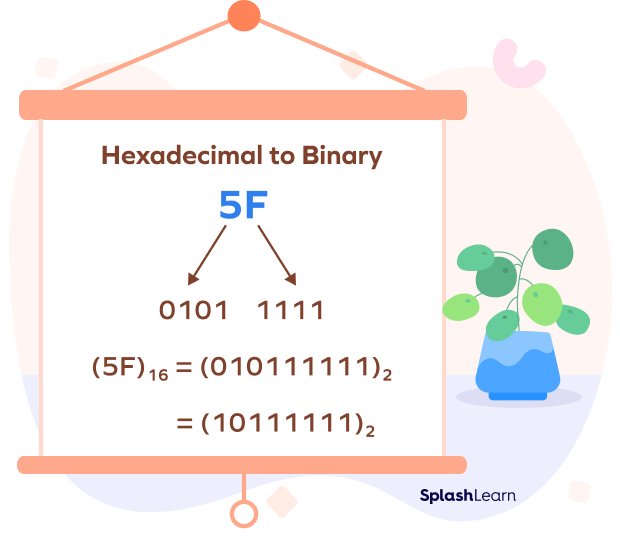
Hexadecimal to Binary Conversion Involving Hexadecimal Point

We can convert a hexadecimal number with a hexadecimal point to the binary system using the conversion table.

Example: Convert (0.A35)₁₆ to binary.

Find the binary equivalent of each digit using the conversion table.

A₁₆ = 1010₂

3₁₆ = 0011₂

5₁₆ = 0101₂

(0.A35)₁₆ = (0.101000110101)₂

Facts about Hexadecimal to Binary Conversion

Conclusion

In this article, we learned about the hexadecimal to binary conversion and two methods to convert a hexadecimal number into binary. Let’s solve a few examples and practice problems to check your understanding.

Solved Examples on Hexadecimal to Binary Conversion

1. Convert (0B)₁₆ into a hexadecimal number system by direct method.

Solution: 

“0” in hexadecimal is equivalent to “0000” in binary.

“A” in hexadecimal is equivalent to “1010” in binary.

So, (0B)₁₆ = (00001011)₂

2. What is the value of (F2)₁₆ into a hexadecimal number system using the indirect method?

Solution:

Hexadecimal to binary:

Here, F = 15

$(F2)_{16} = (15 \times 16^{1}) + (2 \times 16^{0})$

$(F2)^{16} = (15 \times 16) + (2 \times 1)$

$(F2)_{16} = 240 + 2$

$(F2)_{16} = 242_{10}$

Decimal to binary:

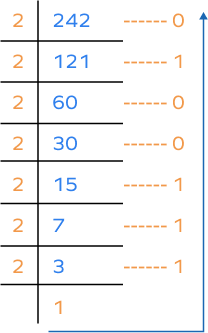
Thus, (F2)₁₆ = 242₁₀ = (11110010)₂

3. Convert (DE)₁₆ into the binary number system.

Solution: 

D₁₆ = 1101₂

E₁₆ = 1110₂ 

So, (11011110)₂ = (DE)₁₆

Practice Problems on Hexadecimal to Binary Conversion

Frequently Asked Questions about Hexadecimal to Binary Conversion