What Is Lattice Multiplication?
We are familiar with the long multiplication method used to multiply large numbers easily. The lattice method is an alternative multiplication method, which is comparatively easy and also interesting.
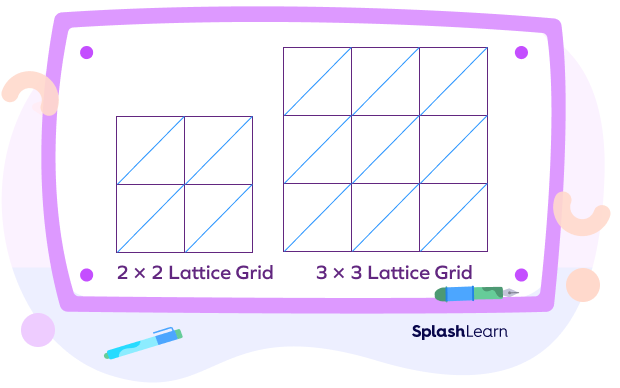
It is called the lattice method because it works by breaking down the numbers being multiplied with the help of a lattice structure. The word “lattice” means a framework or a structure of crossed wood or metal strips as shown below.

Thus, instead of performing a vertical or column multiplication, we use a lattice-like framework as shown below to multiply given numbers. To multiply an m-digit number by an n-digit number, we draw a lattice of order $m \times n$. The smallest grid used is a $2 \times 2$ grid.
Recommended Games
Lattice Multiplication Definition
Lattice multiplication is a method of multiplication in which we use a lattice grid to multiply two or more large numbers. This method is simple and more visual.
Recommended Worksheets
Steps For Lattice Multiplication Method
Let’s see steps for lattice multiplication with the help of an example!
Example: Find $23 \times 36$ using lattice multiplication.
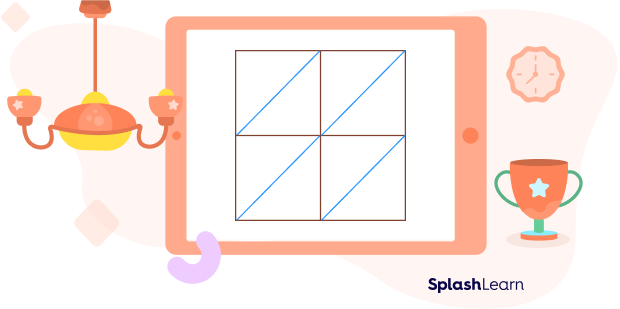
Step 1: Draw the lattice.
The first thing we need to do is to build a grid according to the number of digits we have in each number to be multiplied. As mentioned earlier, to multiply an m-digit number by an n-digit number, we draw a lattice of order m×n.
Here, we are multiplying two two-digit numbers. Thus, we need to draw a 22 grid.
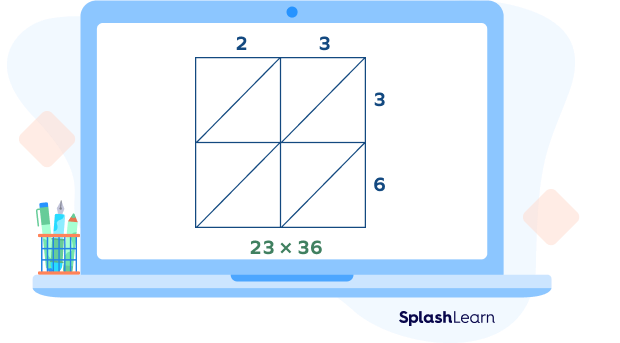
Step 2: Label the lattice.
Now that we have the grid, we need to label it.
Here, we want to multiply 23 and 36 using the lattice method. We assign each digit of the first number to an individual column. Similarly, we name each row using each digit of the second number.
Step 3: Multiply the numbers.
Here, we must understand two things:
- Which numbers to multiply
- How to write the products in the grid
We multiply numbers in the following pattern.
First row $\times$ First Column: $2 \times 3$
First row $\times$ Second Column: $3 \times 3$
Second row $\times$ First Column: $2 \times 6$
Second row $\times$ Second Column: $3 \times 6$
We write these products in the corresponding cells (where the row and column meets) in the following format.Alt tag: Placement of products in lattice grid
The final grid after writing the products looks like this:
Alt tag: Products in lattice multiplication
Step 4: Add the numbers.
Add numbers in each diagonal within the grid and write the sum below. Start at the bottom right corner and write the sum just below it. Extend the diagonals to make some space for writing the sums.
Note: A very important point is if the sum turns out to be two digits, regroup to the next diagonal. In simple words, write the ones digit of the sum and carry over the tens digit to the next diagonal space. Continue this till you reach the top left triangle.
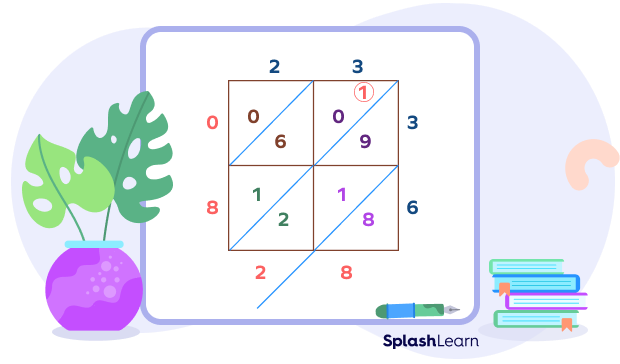
Step 5: Write the final product.
The final product is obtained by reading the numbers from the top left corner to the bottom right.
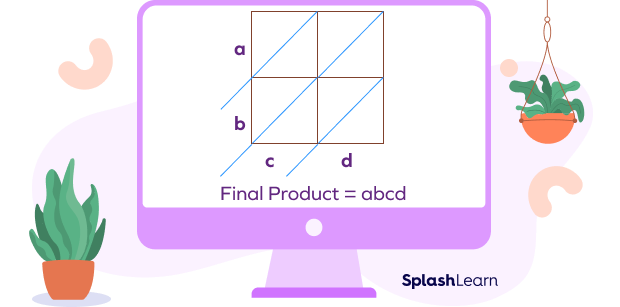
Thus, in the above example, we get
$23 \times 36 = 828$
How to Do Lattice Multiplication
Let’s use the steps we discussed to perform lattice multiplication. We will consider different cases.
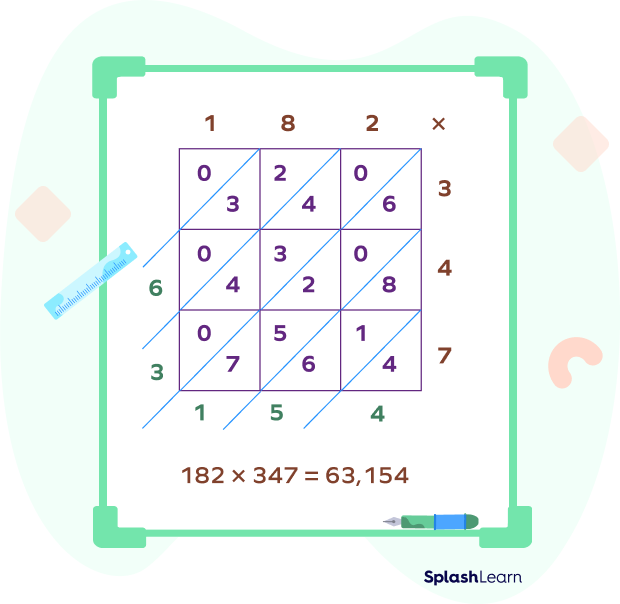
Three-digit Number by a Three-digit Number
Example: $182 \times 347$
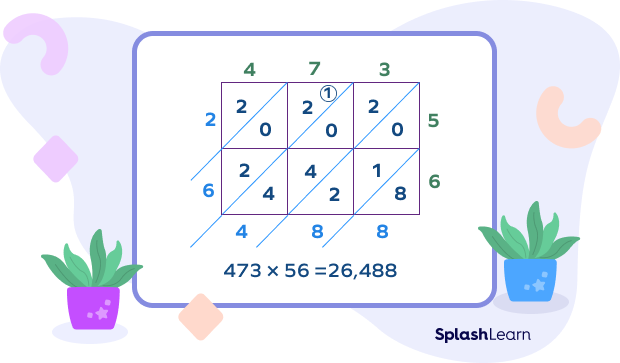
Three-digit Number by a Two-digit Number
Example: $473 \times 56$
How to Multiply Decimals Using Lattice Multiplication
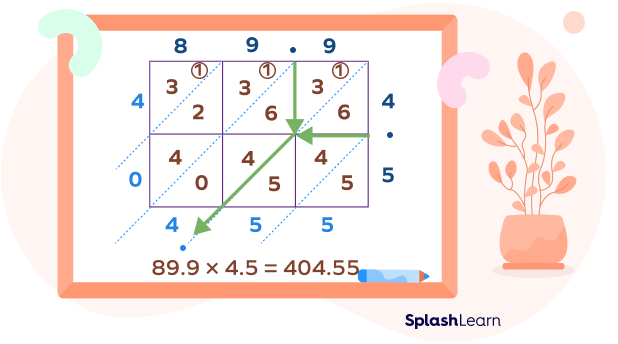
The lattice multiplication of two decimals follows the same steps that we use for multiplying two whole numbers. We just need to understand where to put the decimal point in the final product. We can determine this position using the lattice grid.
Consider an example. Multiply 89.9 and 4.5.
Here, we draw a $3 \times 2$ grid. To determine the position of the decimal point in the answer, draw lines from the decimal points in the given decimals. The diagonal that meets the point of intersection of these lines tells us where to put the decimal point.
Facts about Lattice Multiplication
- Lattice multiplication is believed to have originated in ancient India.
- Lattice multiplication provides a visual representation of the multiplication process.
Conclusion
In this article, we learned about lattice multiplication method step by step with a variety of examples. Let’s revise what we learned with the help of a few examples and practice problems.
Solved Examples on Lattice Multiplication
1. Complete the following lattice grid to find the product of 34 and 17.
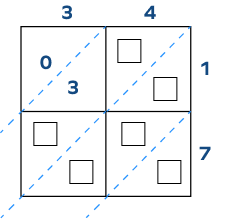
Solution:
We multiply the numbers with the help of rows and columns.
$3 \times 1 = 03$
$4 \times 1 = 04$
$3 \times 7 = 21$
$4 \times 7 = 28$
Write tens digit above the diagonal line and the ones digit below the diagonal line. Next, find the sum of the numbers within diagonals starting from the bottom right.
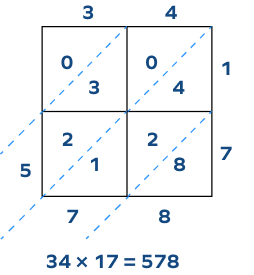
Writing the sums from the top-left to bottom-right, we get 0578, which is 578.
Hence, $34 \times 17 = 578$
2. Find the product of 49 and 19.
Solution:
Draw a $2 \times 2$ grid and label it. Multiply the numbers to fill the grid.
$4 \times 1 = 04;\; 9 \times 1= 09;\; 4 \times 9=36;\; 9 \times 9 = 81$
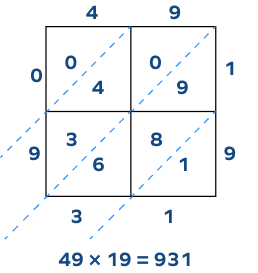
Now, write the numbers from the top-left to bottom-right, we get 0931, which is 931.
Hence, the product of 49 and 19 is 931.
3. Find the product of 97 and 9 using lattice multiplication.

Solution:
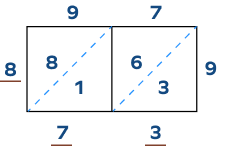
Write the sums from top-left to bottom-right to find the answer.
Hence, the product of 97 and 9 is 873.
4. Find the product of 273 and 49.
Solution:

Read the numbers starting from the top left corner, we get 13377.
Hence, the product of 273 and 49 is 13377.
5. Find the product of 32.5 and 6.
Solution:
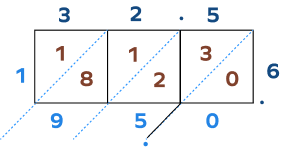
Thus, $32.5 \times 6 = 195$
Practice Problems on Lattice Multiplication
Lattice Multiplication - Definition, Method, Examples, Facts, FAQs
What type of lattice grid will be required to multiply 456 and 9876?
There are 3 digits in the first number and 4 digits in the second.
Thus, a $3 \times 4$ lattice grid will be required.
Where is the tens digit of a product placed in the box inside a lattice grid?
The tens digit of the product is placed above the diagonal line.
The given lattice multiplication shows that $81 \times 47 =$
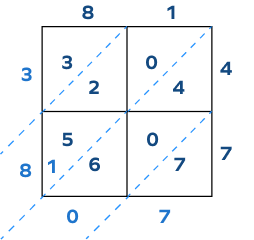
To find the final answer, we write the sums starting from the top-left corner to the bottom-right corner.
$81 \times 47 = 3807$
Lattice method of multiplication is also known as
Lattice method of multiplication is also known as Chinese multiplication.
Which of the following problems can be solved using the lattice method of multiplication?
We can multiply only two numbers using the lattice multiplication method.
Frequently Asked Questions about Lattice Multiplication
What advantages does the lattice multiplication offer?
It breaks down the multiplication problem into smaller and easier steps. Also, it gives a great insight into concepts like place values of numbers, regrouping, etc. It can be used to find the square of large numbers easily.
Why should we use the lattice method of finding the product?
It saves time. It minimizes errors. Also, it is very easy to check for errors. It keeps all the numbers organized in the grid.
What is the Box method of multiplication?
The box method of multiplication appears very similar to the lattice multiplication method. However, in the box method, we break down the numbers using place values or the expanded form. Also, the box method uses a tabular structure to write partial products.
Example: $15 \times 21$
| $\times$ | 20 | 1 |
| 10 | 200 | 10 |
| 5 | 100 | 5 |
$15 \times 21 = 200 + 100 + 10 + 5$
$15 \times 21 = 315$




































