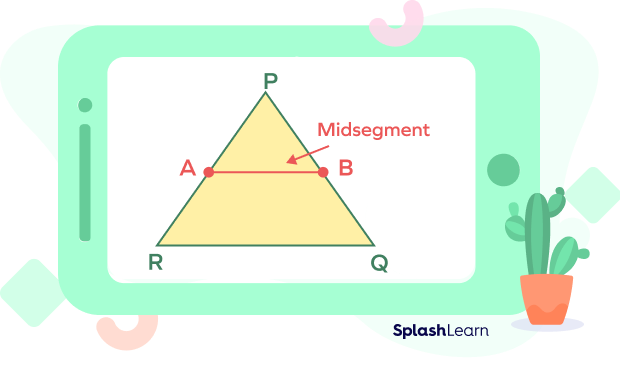
What Is the Midsegment of a Triangle?
The midsegment of a triangle is a line segment joining the midpoints of two sides of the triangle. A triangle has three midsegments.
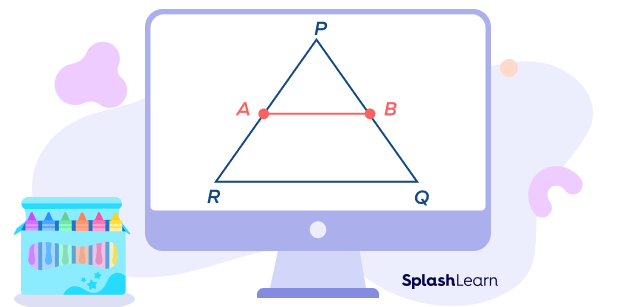
Consider the triangle PQR in the given diagram. The points P, Q, and R are the three vertices of the triangle. PQ, QR, and PR are the three sides. Point A is the midpoint of side PR. Point B is the midpoint of side PQ.
The line segment AB that joins the midpoints A and B. It is the midsegment of the triangle PQR.
Notice that AB is parallel to the side QR.
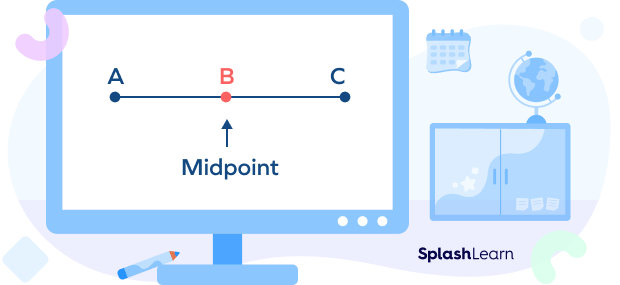
Midpoint is the middle or center point of a line segment that divides it into two equal parts. It is equidistant from both endpoints of a line segment. A triangle is a polygon with 3 sides, 3 angles, and 3 vertices.
Recommended Games
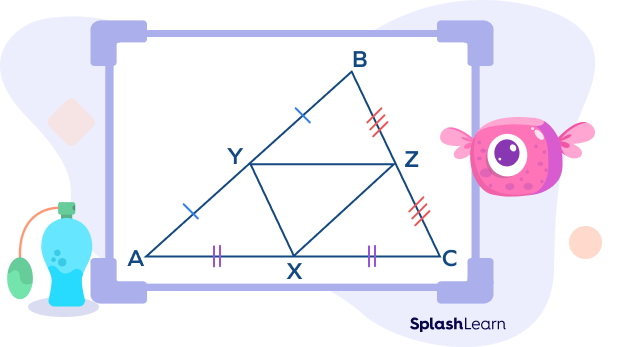
Midsegment of a Triangle: Definition
The midsegment is a line segment that joins the midpoints of any two sides of a triangle.
So, how many midsegments does a triangle have? The answer is 3.
In the triangle ABC shown below, the three midsegments are XY, YZ, and XZ.
Here,
AB || XY
AC || YZ
BC || XZ
Recommended Worksheets
Properties of the Midsegment
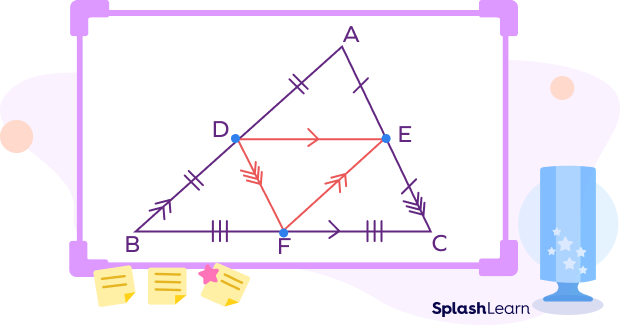
- A triangle has three midsegments.
DE, EF, DF are three midsegments of the triangle ABC.
- A midsegment joins the midpoints of two sides.
D is the midpoint of the side AB.
E is the midpoint of the side AC.
F is the midpoint of the side BC.
- The midsegment of a triangle is always parallel to the third side of the triangle.
DE || BC
EF || AB
DF || AC
- The length of the midsegment is half the length of the third side.
DE $= \frac{1}{2}$ BC
EF $= \frac{1}{2}$ AB
DF $= \frac{1}{2}$ AC
- The three midsegments of a triangle form a triangle similar to the original triangle.
DEF ABC
- The smaller triangle formed by the midsegments is $\frac{1}{4}$th area of the original triangle and half the perimeter of the original triangle.
Area of $\Delta \text{BDF} = \text{Area of} \Delta \text{CEF} = \text{Area of} \Delta ADE = \frac{1}{4} \times \Delta \text{ABC}$
Perimeter of $\Delta \text{BDF} = \text{Perimeter of} \Delta \text{CEF} = \text{Perimeter of} \Delta \text{ADE} = \frac{1}{2} \times \text{Perimeter of} \Delta \text{ABC}$
Midsegment Theorem of a Triangle
Triangle Midsegment Theorem Statement: The line segment joining the midpoints or centers of any two sides of a triangle is parallel to the third side and half of it in length.
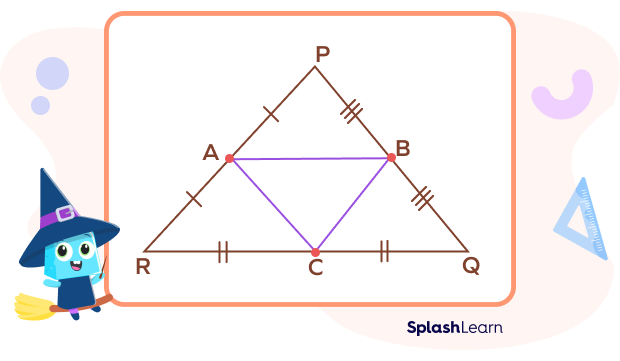
According to the midsegment theorem:
- AB || RQ, AB $= \frac{1}{2}$ RQ
- AC || PQ, AC$= \frac{1}{2}$ PQ
- BC || PR, BC$= \frac{1}{2}$ PR
Proof of Midsegment Theorem of a Triangle
To prove:
In the triangle PQR,
- AB || RQ
- AB $= \frac{1}{2}$ RQ
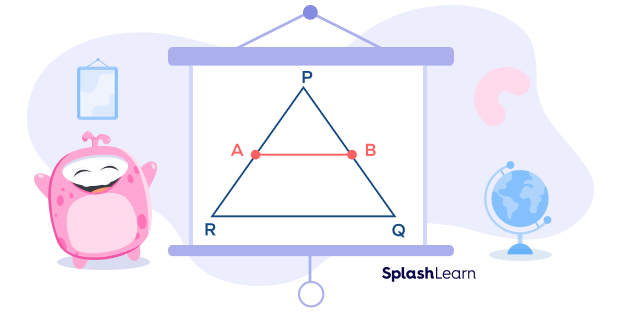
Construction: Extend the line AB from the point B. Construct a line QC parallel to AR, such that it meets the extended line AB at point C.
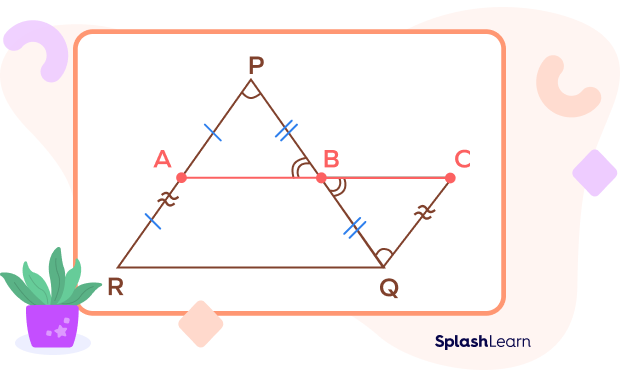
A is the midpoint of PR. B is the midpoint of PQ.
In $\Delta PAB$ and $\Delta QCB$
$PB = BQ$ $\therefore$ B is the midpoint of PQ
$\angle APB = \angle CQB$ $\therefore$ Alternate angles
$\angle ABP = \angle CBQ$ $\therefore$ Vertically Opposite angles
Therefore, by AAS congruence criteria of a triangle, we have
$\Delta ADE \cong \Delta CFE$.
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent),
$PA = QC$ and $AB = BC$ …(1)
Now, we have
$PA = AR$ A is the midpoint of PR. …(2)
$PA = QC$ from (1) …(3)
We can say that
$PA = AR = CQ$ …from (1),(2),(3)
As AC || RQ, AR || CQ, and AR = CQ, we can say that ACQR is a parallelogram.
Therefore, AC = RQ.
Here, $AB = \frac{1}{2}$ AC and AC = RQ
Hence, $AB = \frac{1}{2}$ RQ
Also, as ACRQ, we have ABRQ
Hence proved.
Converse of Midsegment Theorem of a Triangle
Converse of the midsegment theorem: If a line segment joining any two sides of a triangle is parallel to the third side and is half the length of the third side, then it is the midsegment of the triangle.
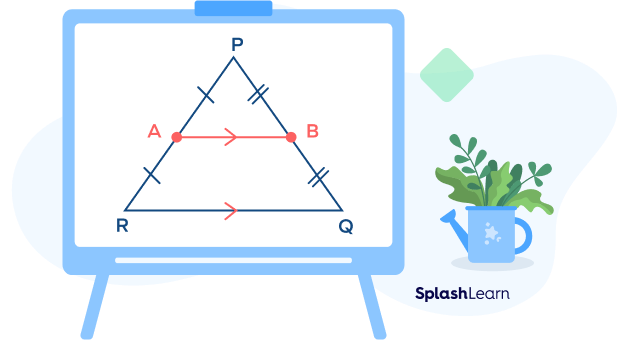
In $\Delta PQR$, if A is the midpoint of sides PR, AB || RQ and $AB = \frac{1}{2}\; RQ$, then AB is the midsegment of the $\Delta PQR$.
Proof of Converse of Midsegment Theorem
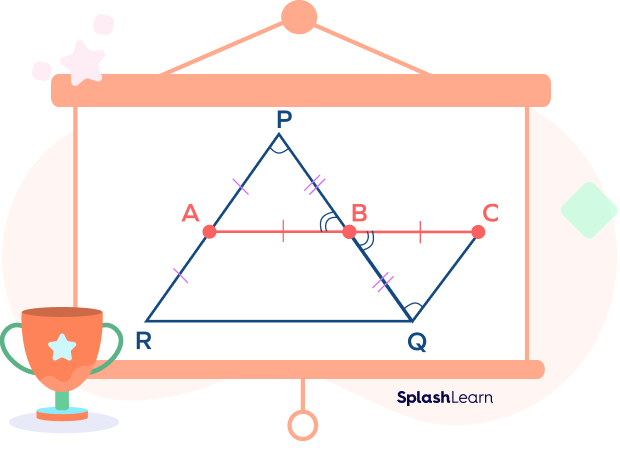
Given: In triangle PQR, AB joins two sides PR and PQ of a triangle PQR.
AB || QR
$AB = \frac{1}{2} \times QR$
To prove: AB is the midsegment of $\Delta PQR$.
OR
B is the midpoint of PQ and A is the midpoint of PR.
Construction: Extend the line AB from the point B to the point C, such that $AB = BC$.
Construct a line QC parallel to AR, such that both lines meet at point C.
It is given that A is the midpoint of PR, AB || RQ and AB $= \frac{1}{2}$ RQ.
$AB = BC$ …construction
$AB = \frac{1}{2} RQ$ …Given
Thus, $AC = QR$
Also, AR || CQ …Given
AB || RQ …Construction
Therefore, DBCF is a parallelogram.
We know that opposite sides of a parallelogram are parallel and equal.
Therefore, $AR = CQ$ and PA || CQ …(1)
In $\Delta PAB$ and $\Delta QBC$,
$\angle APB = \angle CQB$ (Alternate angles)
$AB = BC$
$\angle PBA = \angle QBC$ (Vertically opposite angle)
So, by AAS congruence criterion, $\Delta PAB \cong \Delta QBC$
Using CPCTC, we write
$PB = BQ$
$CQ = AP$
But $AR = CQ$ …from (1)
Thus, $AP = AR$
Therefore, AB is the midsegment of $\Delta PQR$.
How to Find the Midsegment of a Triangle
To construct the midsegment of a triangle, we find midpoints of any two sides of the triangle.
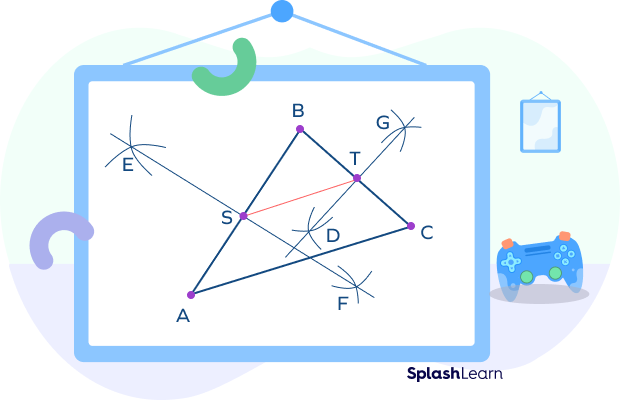
Step 1: Put the compass on the vertex B. Keep the compass distance more than half the length of BC. Draw arcs on both sides of BC. Draw similar arcs keeping the compass on the vertex C to intersect the previous arcs at points D and G respectively. Draw a line joining the points D and G. Let the line DG intersect the side BC at the point T. T is the midpoint of the side BC.
Step 2: Similarly, find the midpoint of the side AB. Let S be the midpoint of side AB.
Step 3: Join S and T. The segment joining S and T is the midsegment of the triangle ABC.
Midsegment Formula
The formula to find the length of the midsegment is
Length of the midsegment $= \frac{1}{2} \times$ Length of the base of triangle
Facts about the Midsegment of a Triangle
- The triangle formed by joining the midsegments of an equilateral triangle is an equilateral triangle.
- The midsegment of a triangle theorem is also known as the mid-point theorem.
Conclusion
In this article, we learned about the midsegment of a triangle. It is the line that joins the midpoints or center of any two sides of a triangle. Let’s solve a few examples of the midsegment of a triangle for a better understanding!
Solved Examples on Midsegment of a Triangle
1. Find the value of x if MN is the midsegment of the triangle XYZ.
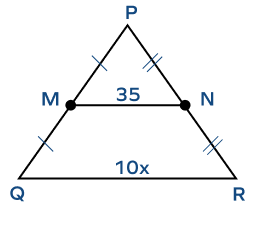
Solution: According to the midsegment theorem, the length of the midsegment is half the length of the third side.
$MN = \frac{1}{2} \times QR$
QR $= 2$ MN
$10x = 2 \times 35$
$10x = 70$
$x = 7$ units
2. In the triangle below it is given that BC $= 36$cm, and M, N are the midpoints of AB and AC. Find XY.
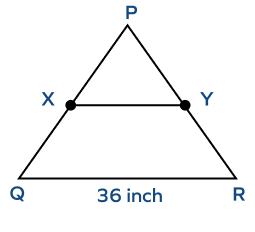
Solution: According to the midsegment theorem, the length of the midsegment is half the length of the third side.
$XY = \frac{1}{2}\; BC$
$XY = \frac{1}{2} \times 36$
$XY = 18$ in
3. AB is the midsegment of the triangle ABC. Find the value of x.
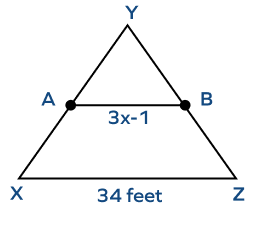
Solution:
According to the midsegment theorem, the length of the midsegment is half the length of the third side.
$AB = \frac{1}{2} \times XZ$
$3x \;-\; 1 = \frac{1}{2} \times 34$
$3x \;-\; 1 = 17$
$3x = 18$
$x = 6$ feet
4. If ABC is an equilateral triangle with a midsegment of length 12 units then find the perimeter of the triangle ABC.
Solution:
According to the midsegment theorem,
Length of the midsegment $= \frac{1}{2} \times$ length of the base of triangle
Let the side of the equilateral triangle be x.
$12 = \frac{1}{2} \times x$
$x = 2 \times 12$
$x = 24$ units
Perimeter of an equilateral triangle $= 4x = 4 \times 24 = 96$ units
5. Find the perimeter of $\Delta DEF$, if the perimeter of $\Delta ABC$ is 72 units.
DE, EF, and DF are midsegments.
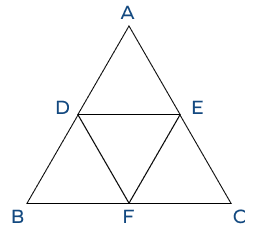
Solution:
By the midsegment theorem, we have
DE || BC and DE $= \frac{1}{2}\times$ BC —————— (i)
Similarly,
DF || AC and DF $= \frac{1}{2}\times$ AC —————— (ii)
and
EF || AB and EF $= \frac{1}{2} \times$ AB —————— (iii)
Now, the perimeter of $\Delta DEF = DE + EF + FD$
$\Rightarrow$ Perimeter of $\Delta DEF = \frac{1}{2} BC + \frac{1}{2} AC + \frac{1}{2} AB$ (from equation i, ii and iii)
$\Rightarrow$ Perimeter of $\Delta DEF = \frac{1}{2} (BC + AC + AB)$
$\Rightarrow$ Perimeter of $\Delta DEF = \frac{1}{2}$ $(\text{Perimeter of} \Delta ABC) = \frac{1}{2} \times 72 = 36$ cm.
Practice Problems on Midsegment of a Triangle
Midsegment of a Triangle: Definition, Theorem, Formula, Examples
In the triangle LMN, if OP is the midsegment, which of the following statements is true?
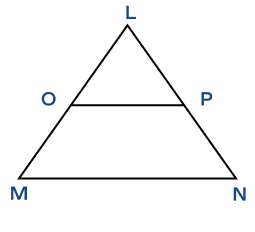
According to the midsegment theorem, the length of the midsegment is half the length of the third side.
$2OP = MN$.
The triangle formed by joining the midsegments of an equilateral triangle is _____.
The triangle formed by joining the midsegments of an equilateral triangle is an equilateral triangle.
If ABC is an equilateral triangle with a perimeter of 45 units. Find the length of its midsegment.
Perimeter of an equilateral triangle $= 3\times$ side
$45 = 3 \times$ side
Thus, side $= 15$
Length of the midsegment $= \frac{1}{2}\times$ length of the base of triangle
Midsegmen $= \frac{1}{2} \times 15 = 7.5$ units
A triangle has ______ midsegments.
A triangle has 3 midsegments.
Frequently Asked Questions about Midsegment of a Triangle
How many midsegments does a triangle have?
A triangle has three midsegments.
How many midsegments does a triangle have?
The formula to find the length of the midsegment is
Length of the midsegment $= \frac{1}{2} \times$ Length of the base of triangle
Are all the midsegments of a triangle equal in length?
All the midsegments of a triangle are equal in length only in the case of an equilateral triangle. In an isosceles triangle, two midsegments are equal in length whereas, in a scalene triangle, no midsegments are equal.
What are some applications of the midsegment theorem of a triangle and its converse?
The midsegment in geometry is a concept that can be used to find missing side lengths in triangles, to determine if a triangle is isosceles, and to find the center of a triangle. It can also be used in engineering and architecture to design structures with specific properties.
How long is the midsegment of a triangle?
The midsegment of a triangle is half the length of the third side.



























