Tenths – Definition with Examples

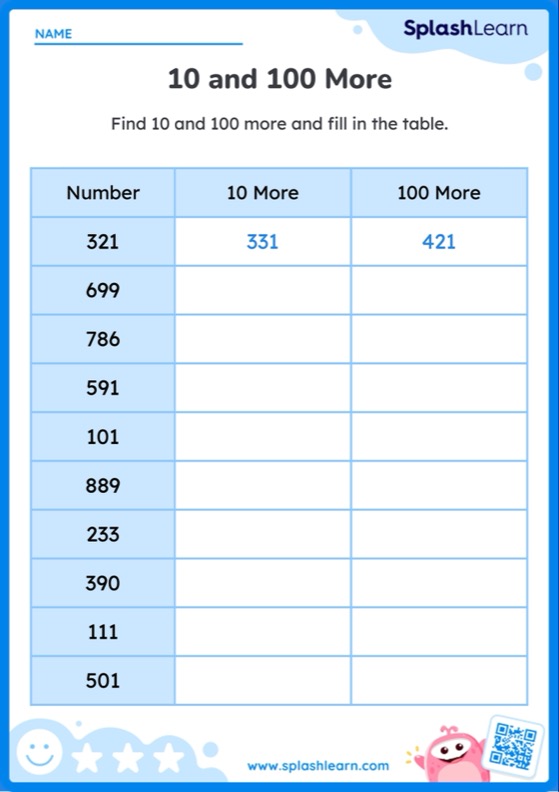
What Is the Tenths Place in a Decimal?

The first place immediately to the right of the decimal point is the tenths place. The term “tenths” in math is also used for describing decimal fractions with a denominator of 10. Tenths are decimals with only one decimal digit. 

One-tenth is a decimal that represents one part out of 10 equal parts.

One-tenth as a fraction $= \frac{1}{10}$

One-tenth as a decimal $= 0.1$

One-tenth as a percentage $= 10\%$

Examples: 

In the decimal 0.7, the digit “7” is in the tenths place, indicating seven-tenths. 

Tenths: Definition

The tenths place in decimals is the first place after the decimal point. Tenths are decimals with only a single decimal digit.

Examples:

Three-tenths: 0.3

2.1: Two and one tenth

7.9: Seven and nine tenths

Tenths: Place Value in Decimals

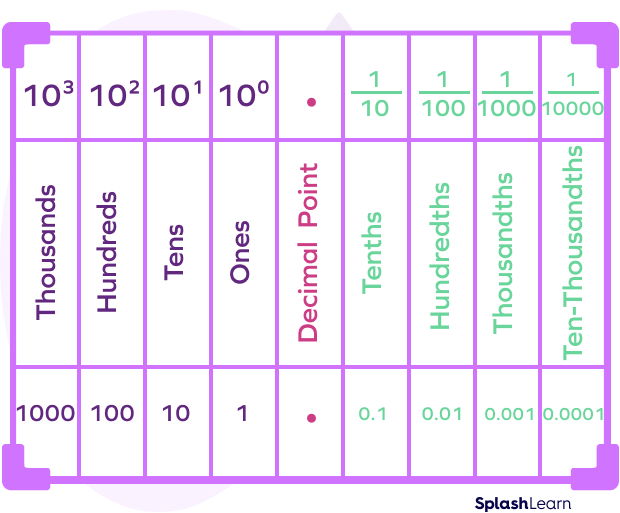
In the decimal number system, each digit’s place value is represented in terms of powers of 10. It is one of the ten equal parts into which a whole number or one whole unit can be divided in the decimal system.

In decimal place values, the tenths place refers to the first place to the right of the decimal point, right before the hundredth place.

Example: In the decimal number 2.3, the digit “3” is in the tenths place, indicating that there are three-tenths or $\frac{3}{10}$. 

$2.3 = 2 + \frac{3}{10} = 2 + 0.3$

Ones	Decimal Point	Tenths
2	.	3

One-tenth: Place Value Chart

One-tenth means one part in ten equal parts. The decimal form is 0.1. The fraction form is 110.

Take a look at the tenths place chart given below:

Ones	Decimal Point	Tenths
0	.	1

Visual Representation of One Tenth

To represent one-tenth visually, divide the given shape (circle, bar) into 10 equal parts and shade only one part.

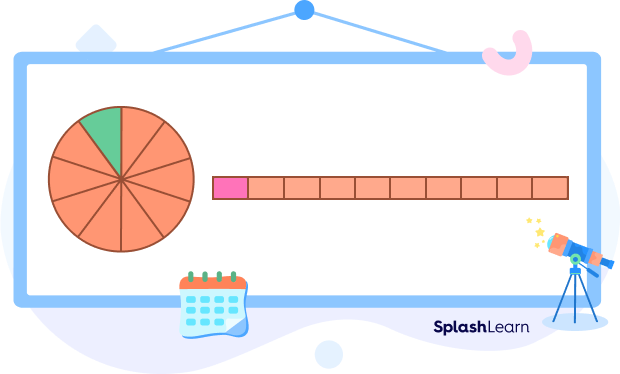
Similarly, to represent 0.1 or one-tenth on a number line, we divide the segment joining 0 and 1 into 10 equal parts. The first marking represents 0.1.

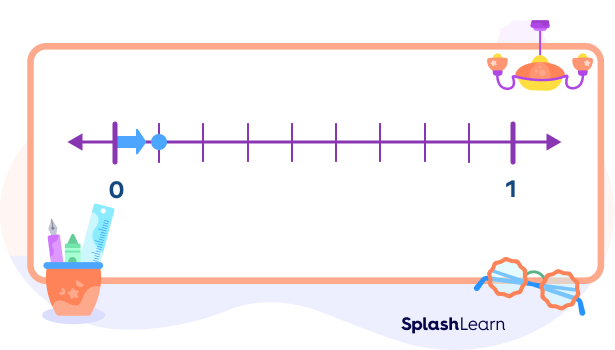
Place Value Blocks for Representing Tenths

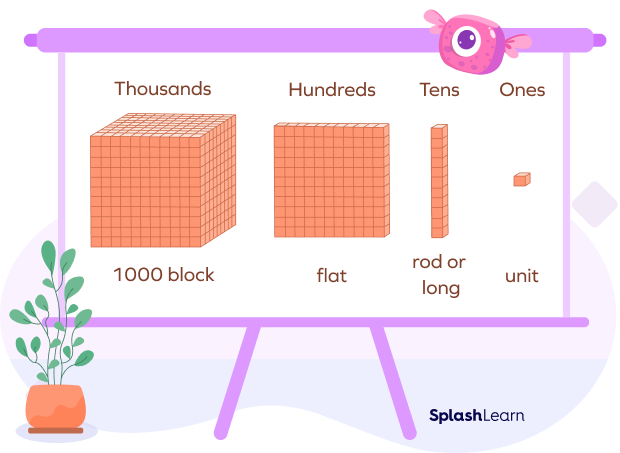
Place value blocks for representing tenths are valuable tools for teaching place values.

These blocks come in four sizes: unit (cube), rod, flat, and cube, each ten times larger than the previous. 

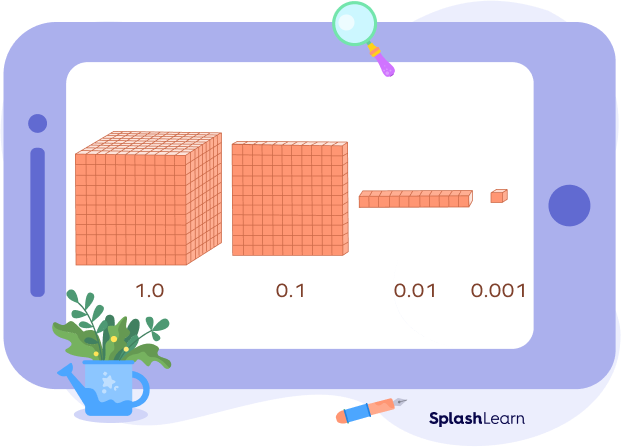
When learning place values in decimals, the values of the pieces may be renamed. If the cube is given a value of 1, then the flat would represent one-tenth or 0.1, and the rod would represent one-hundredth or 0.01.

Tenth as an Ordinal Number

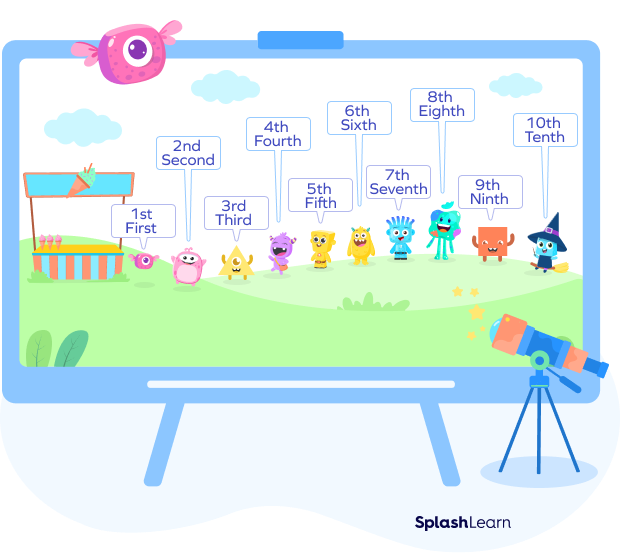
So far, we discussed the term “tenths” with respect to decimal place values. In daily life, when we have to indicate the position of an object, we use terms like first, second, third, etc. Similarly, to indicate the 10^th rank, we use the term “tenth.”

Numbers that are used to represent the rank or position of an object or a person are called ordinal numbers.

“Tenth” can be used as both a cardinal number (to denote quantity) and an ordinal number (to denote position or order). As an ordinal number, “tenth” indicates the position of an item in a sequence, where it is the 10^th item in that sequence. 

Example 1: The tomato soup recipe is on the book’s tenth page.

Example 2: Representing positions of people standing in a queue.

Rounding Decimals to the Nearest Tenth

When working with decimals, we sometimes use rounding for convenience. Rounding to the nearest tenth means keeping one digit after the decimal point.  In other words, we are approximating the decimal to the closest tenth value. Let’s see how to round the decimals to their nearest tenths.

• Step 1: Identify the digit in the tenths place.

The tenths place is the first digit to the right of the decimal point. 

• Step 2: Identify the digit in the hundredths place.

Examine the digit immediately to the right of the tenth place. 

If this digit is 5 or greater, we round up. 

If it is less than 5, we round down.

• Step 3: Rounding up or round down.

i) If the digit to the right is 5 or greater, round up (add 1 to the tenths-place digit and change the hundredths place to 0.) 

ii) If the digit to the right is less than 5, round down (keep the tenths-place digit the same and change the hundredths place to 0.)

Example: Round 3.24 to the nearest tenth. 

The digit at the tenths place = 2

The digit at the hundredths place = 4 < 5

Thus, we round down.

3.24 rounded to the nearest tenth is 3.2.

Example 2: 3.76 rounded to the nearest tenth is 3.8 because 6 > 5.

Example 3: 3.55 rounded to the nearest tenth is 3.6 since the digit at the hundredths place = 5.

Example 4: 3.24 rounded to the nearest tenth is 3.2 because 2 < 5.

Facts about Tenths Place

Solved Examples on Tenths Place

Example 1: Express​ $\frac{7}{10}$  as a decimal and word form.

Solution:

The decimal form of $\frac{7}{10}$ is 0.7.

The word form of $\frac{7}{10}$ is seven-tenths.

$\frac{7}{10} = 0.7 =$ Seven-tenths

Example 2: How many hundredths are there in a one-tenth? 

Solution:

One-tenth $= \frac{1}{10} = 0.1$

One-hundredth $= \frac{1}{100} = 0.01$

To find how many 0.01 make a 0.1, divide 0.1 by 0.01.

$\frac{0.1}{0.01} = \frac{1}{10} \times \frac{100}{1} = \frac{1}{10}$

Thus, 10 one-hundredths make a one-tenth.

Example 3: Write the following fractions as a decimal number: $\frac{3}{10} + \frac{6}{10} + \frac{9}{10}$

Solution: 

The fractions have the same denominator. We will add the numerators, keeping the same denominator.

$\frac{3}{10} + \frac{6}{10} + \frac{9}{10} = \frac{18}{10} = 1.8$ 

So, $\frac{3}{10} + \frac{6}{10} + \frac{9}{10}$  as a decimal number is 1.8 or one and eight tenths.

Practice Problems on Tenths Place

Frequently Asked Questions about Tenths