Perimeter of a Semicircle – Definition, Formula, Examples, Facts

What Is the Perimeter of a Semicircle?

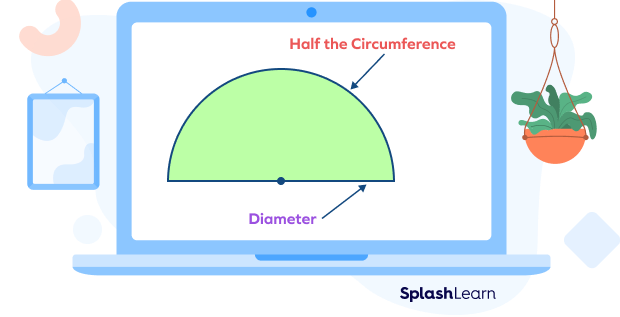
Perimeter of a semicircle is the total length of its boundary, which is composed of half of the circumference of the circle and the length of the diameter.

Perimeter of a semicircle $= \pi r + 2r$

What is a semicircle?

When a circle is divided into two equal halves by the diameter, each half is called a semicircle. A semicircle is simply a half circle.

What is the perimeter?

The perimeter describes the total length of the boundary of a 2D figure. The perimeter of a circle is known as its circumference.

Perimeter of a Semicircle Formula

Perimeter of a semicircle $=$ half of the circumference of the circle $+$ diameter 

Perimeter of a semicircle $= \pi r + d$

Perimeter of a semicircle $= \pi r + 2r$

where “r” is the radius of the circle.

How to Find the Perimeter of a Semicircle

Let’s understand how to find the perimeter of a half circle.

Step 1: Find the half the perimeter (circumference of the circle).

Step 2: Find the length of the diameter.

Step 3: Add the values obtained in step 1 and step 2.

Step 4: Give the appropriate unit based on the unit of the radius.

Perimeter of a Semicircle Is Not Half the Perimeter of the Circle

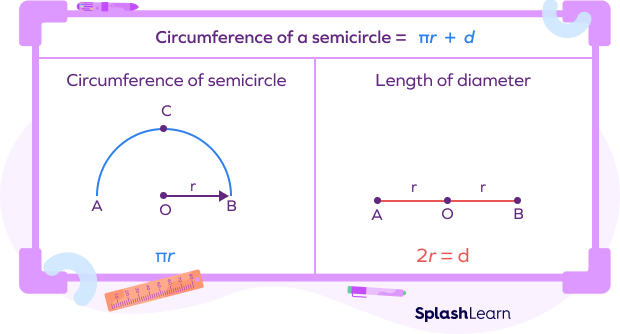
Semicircle is half of a circle, but the perimeter of a semicircle is not half of the perimeter of the circle. 

Half the perimeter of a circle only represents the curved part of the semicircle. 

Perimeter of a circle $= 2\pi r$. 

Half the perimeter of the circle $= \frac{1}{2} \times 2\pi r = \pi r$

The semicircle also has diameter as part of its boundary. We need to add the length of the diameter to get the total perimeter of the semicircle.

Length of the diameter $= d = 2r$              d is the diameter, r is the radius

Let’s visualize this to get a better idea!

Finding the Perimeter of a Semicircle When Area Is Given

Area of a circle $= \pi r^{2}$

Semicircle is half the circle.

So, area of semicircle $= \frac{1}{2} \times \pi r^{2}$ ….(1)

Suppose the area of the semicircle is 77 square inches. 

We will find the radius using the formula (1).

So, $= \frac{1}{2} \times \pi r^{2} = 77$

$\pi r^{2} = 154$

$\frac{22}{7} \times r \times r = 154$

$r = 7$ inches

Substitute $r = 7$ in the formula of perimeter of a semicircle. 

In this case, we get 

Perimeter of semicircle $= \pi r + 2r$

Perimeter of semicircle $= \frac{22}{7} \times 7 + 2 \times 7$

Perimeter of semicircle $= 22 + 14$

Perimeter of semicircle $= 36$ inches

Facts about Perimeter of a Semicircle

Solved Examples on Perimeter of a Semicircle

1. Find the perimeter of the given semicircle.  

Solution: 

Radius $(r) = 0.7$ inches

Perimeter $= \pi r + 2r$

Perimeter $= \frac{22}{7} \times 0.7 + 2 \times 0.7$

Perimeter $= 2.2 + 1.4$

Perimeter $= 3.6$ inches

2. What is the perimeter of a semicircle with diameter 21 inches?

Solution: 

Diameter $= 21$ inches 

Radius $(r) = \frac{Diameter}{2} = 10.5$ inches

Perimeter $= \pi r + d$

Perimeter $= \frac{22}{7} \times 10.5 + 21$

Perimeter $= 33 + 21$

Perimeter $= 43$ inches

3. If the perimeter of the semicircle is 7.2 feet, then find the radius of the circle. 

Solution: 

Perimeter of the semicircle $= 7.2$ feet

Let the radius of the semicircle be r feet.

$r(\pi + 2) = 7.2$

$r(\frac{22}{7} + 2) = 7.2$

$r(\frac{22 + 14}{7}) = 7.2$

$r \times \frac{36}{7} = 7.2$

$r = \frac{7.2 \times 7}{36}$ 

$r = 1.4$ feet

4. If the perimeter of the semicircle is 28.8 inches, find the diameter of the circle.

Solution: 

Perimeter of the semicircle $= 28.8$ inches

Let the radius of the semicircle be r inches and diameter be d inches.

$r (\pi + 2) = 28.8$

$r (\frac{22}{7} + 2) = 28.8$

$r (\frac{22 + 14}{7}) = 28.8$

$r\times \frac{36}{7} = 28.8$

$r = \frac{28.8 \times 7}{36} = 5.6$ inches

We know that

$d = 2r$

$\Rightarrow d = 2 \times 5.6 = 11.2$ inches

5. If the area of the circle is 7546 square units, what is the perimeter of the semicircle?

Solution: 

Area of the circle $= \pi r^{2}$

$7546 = \pi r^{2}$

$7546 = \frac{22}{7} \times r \times r$

$\frac{7546 \times 7}{22} = r \times r$

$2401 = r^{2}$

$r = 49$ units

Practice Problems on Perimeter of a Semicircle

Frequently Asked Questions about the Perimeter of a Semicircle