Perimeter of Isosceles Triangle – Definition, Examples, Facts, FAQs

What Is the Perimeter of an Isosceles Triangle?

The perimeter of an isosceles triangle is the sum of all its sides. It is given by $2x + y$, where x is the length of two equal sides and y is the length of the remaining side.

The perimeter is defined as the total length of the boundary of a shape. It is the sum of all the sides of the shape. A triangle is a polygon with three sides. So, what is the formula for perimeter of a triangle? It is simply the sum of all three sides of the triangle. 

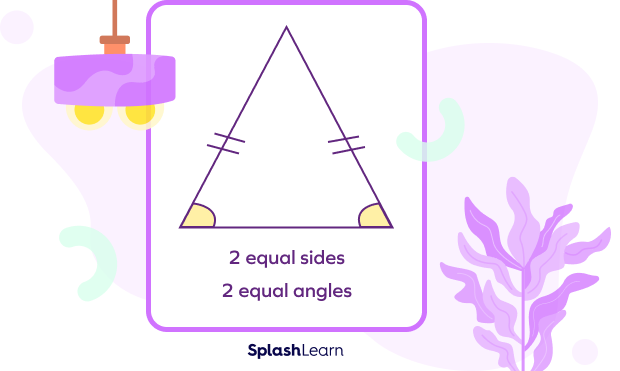
An isosceles triangle is a type of triangle that has two sides of the same length. Also, the angles opposite to the equal sides (known as the base angles) are congruent.

In the given $\Delta ABC$, AB and AC are two equal sides. Angles B and C are congruent.

Perimeter of an Isosceles Triangle Formula

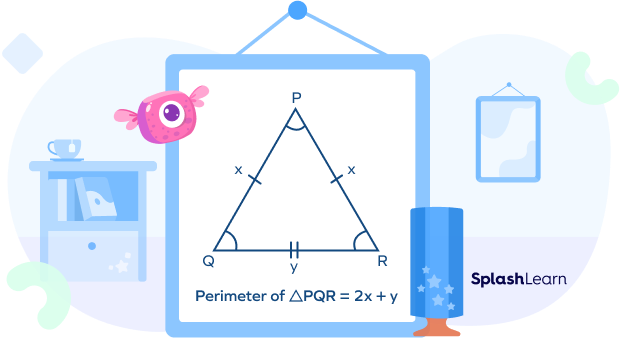
The formula for the perimeter of an isosceles triangle is given by 

Perimeter $= 2x + y$

where, x is the length of the equal sides and y is the unequal side of the isosceles triangle. 

Perimeter is measured in linear units such as inches, yards, etc., same as the length of the sides of the triangle.

Derivation of the Formula for Perimeter of an Isosceles Triangle

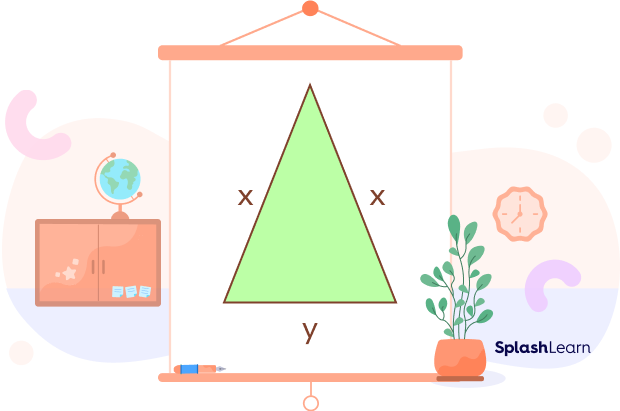
We know that the perimeter of a triangle is the sum of all its sides. Thus, if the side-lengths of a triangle are given by x, y, and z, then we can find the perimeter as

Perimeter of a triangle $= (x + y + z)$ units

Now, take a look at the isosceles triangle shown below where two sides are equal.

Thus, substitute $x = z$

Perimeter of an isosceles triangle $= x + y + x =  (2x + y)$ units

How to Find the Perimeter of an Isosceles Triangle

Step 1: Note down the lengths of sides. Let the “x” be the length of equal sides, and “y” be the length of the unequal side. Make sure that all the sides have the same unit. 

Step 2: Substitute the values in the formula. 

Perimeter of an isosceles triangle $= (2x + y)$ units.

Step 3: Assign the appropriate unit, which will be the same as the length of the sides.

Perimeter of Isosceles Right Triangle

Isosceles right triangle, as the name itself suggests, is a triangle with one right angle and two equal sides.

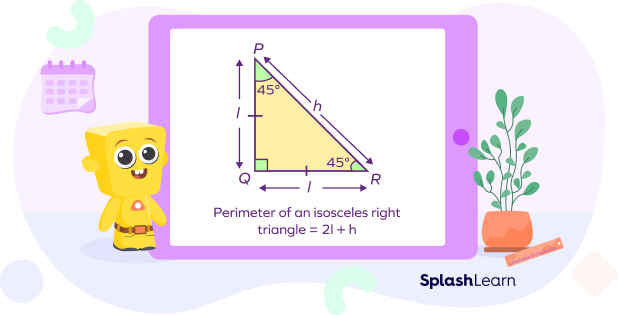
In the given isosceles right triangle PQR, the sides PQ and QR are equal. These sides represent the legs (base and altitude) of the right triangle. The angle Q is a right angle.

Perimeter of an isosceles right triangle $= 2l + h$

If we don’t know the length of the hypotenuse, we can find it using Pythagoras’ theorem.

By Pythagoras’ theorem, 

$Hypotenuse^{2} = Base^{2} + Perpendicular^{2}$

Thus, $h^{2} = l^{2} + l^{2}$

$h^{2} = 2l^{2}$

$h = \sqrt{2\;l}$

Calculating the Perimeter of an Isosceles Right Triangle if Hypotenuse Is Given

We have $h = \sqrt{2\; l}

Thus, $l = \frac{h}{\sqrt{2}}$

Perimeter $= h + 2 \frac{h}{\sqrt{2}} = h (1 + \frac{2}{\sqrt{2}})$

Perimeter of isosceles right triangle $= h (1 + \sqrt{2})$

Calculating the Perimeter of an Isosceles Right Triangle if Length Is Given

We have h = 2 l 

We can rewrite the formula  $(2l + h)$ as

Perimeter $= 2l + \sqrt{2\; l}$

Perimeter of an isosceles right triangle $= (2 + \sqrt{2})\;l$

Finding the Perimeter of an Isosceles Triangle with Base and Height

If we know the base and height, all we need to find here is the length of the equal sides.

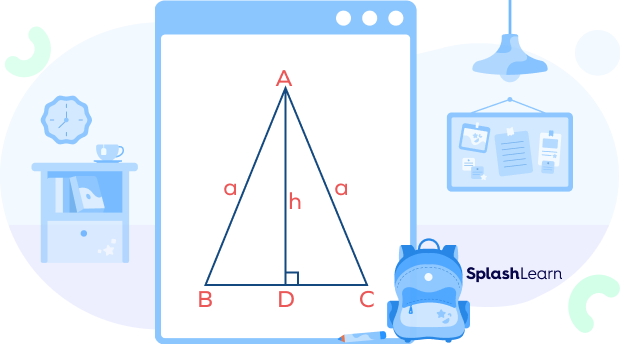
In the isosceles triangle $\Delta ABC,\; AB = AC = a$

$BC = b$ is the base.

Consider the right triangle $\Delta ADC$.

$AD^{2} + CD^{2} = AC^{2}$ …Pythagoras theorem

$h^{2} + (\frac{b}{2})^{2} = a^{2}$

$a^{2} = h^{2} + \frac{b^{2}}{4} = \frac{4h^{2} + b^{2}}{4}$

Thus, $a = \sqrt{\frac{4h^{2} + b^{2}}{2}}$ …length of equal side

Perimeter $= 2 \times \sqrt{\frac{4h^{2} + b^{2}}{2}} + b = \sqrt{4h^{2} + b^{2} + b}$, where b is the base of the triangle and h represents altitude or height of the isosceles triangle. 

Facts about Perimeter of an Isosceles Triangle

Conclusion

In this article, we learned about the perimeter of an isosceles triangle, its formula and steps for calculation. An isosceles triangle has two equal sides. The perimeter of the isosceles triangle is the sum of lengths of all sides. Let’s solve a few examples and practice problems.

Solved Examples on Perimeter of an Isosceles Triangle

1. What is the perimeter of an isosceles triangle if the base is 10 feet and equal sides are 5 feet long?

Solution: Perimeter of isosceles triangle $= (2 \times measure of equal side) + (measure of unequal side)$

Perimeter of isosceles triangle $= (2 \times 5) + 10$

Perimeter of isosceles triangle $= 10 + 10$

Perimeter of isosceles triangle $= 20$ feet

2. What is the perimeter of the right angle isosceles triangle if the hypotenuse is 3 feet. 

Solution: The formula of the perimeter of the right angle isosceles triangle if hypotenuse is given

$= h (1 + \sqrt{2})$.

Perimeter $= 3 (1 + \sqrt{2})$

We know $\sqrt{2} \simeq 1.4$

Perimeter $= 3 (1 + 1.4)$

Perimeter $= 3 \times 2.4$

Perimeter $= 7.2$ feet 

3. What is the measurement of two sides of an isosceles triangle if the perimeter is 60 feet and the base is 25 feet?

Solution: We will put the values in the formula to know the measurement of the sides of an isosceles triangle. 

$60 = 2x + 25$

$2x = 60 \;-\; 25$

$2x = 35$

$x = \frac{35}{2}$

$x = 17.5$ feet   

Thus, the two sides of the isosceles triangle are 17.5 feet each. 

4. Calculate the perimeter of a triangle with two equal sides of 4 inches and a base of 3 inches.

Solution: It is an isosceles triangle. The perimeter is:

Perimeter $= (2 \times 4) + 3$

Perimeter $= 8 + 3$

Perimeter $= 11$ inches

Thus, the perimeter of an isosceles triangle is 11 inches. 

Practice Problems on Perimeter of an Isosceles Triangle

Frequently Asked Questions on Perimeter of an Isosceles Triangle