What Is a Rectangular Pyramid?
A pyramid whose base is in the shape of a rectangle and sides in the shape of a triangle is called a rectangular pyramid.
When we think of pyramids, we think of the Great Pyramids of Egypt, don’t we? Every time we view different pyramids, we can observe how each of its sides are triangular, but the base is different.
So, what does a rectangular pyramid look like? Take a look at the image given below. If the base of a pyramid is a rectangle, it is a rectangular pyramid.

Recommended Games
Rectangular Pyramid: Definition
A rectangular pyramid is a three dimensional solid with its base in the shape of a rectangle and sides in the shape of a triangle.
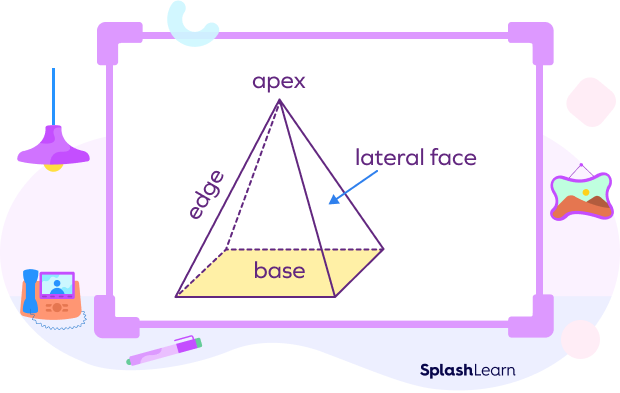
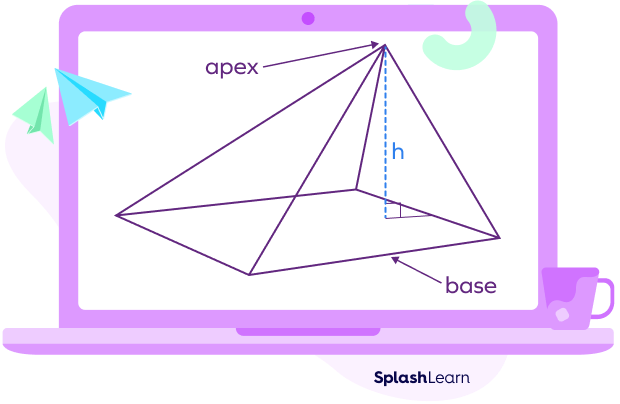
The lateral faces are triangular in shape. A rectangular pyramid is crowned at the top at a point known as the apex. Except for the base, all the faces connect at a vertex at the top called the apex.
Recommended Worksheets
Properties of a Rectangular Pyramid: Faces, Edges, Vertices
Let’s briefly discuss the following three features of a rectangular pyramid.
Faces
The flat surfaces that are created at the edges of a rectangular pyramid are its faces.
The lateral faces of a rectangular pyramid are triangular.
The base is rectangular.
So, how many faces does a rectangular pyramid have? Let’s find out.
Number of lateral triangular faces $= 4$
Number of bases $= 1$
Total number of faces $= 5$
Note that not every triangular face is of the same shape because the base is a rectangle. The opposite faces do, however, have the same shape since the opposite sides of a rectangle are equal in length.
Vertices
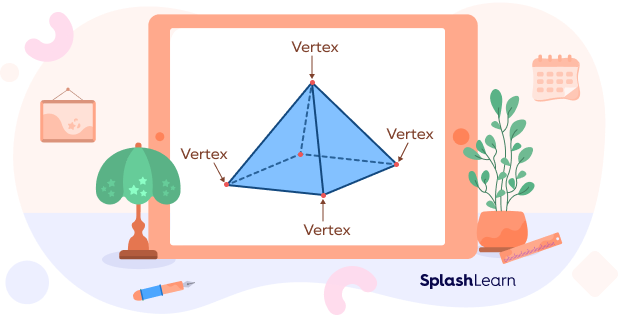
A vertex is a point where two or more edges meet. A rectangular pyramid has 5 vertices. 4 vertices are located at the corner of base and the top vertex is formed by the intersection of the four edges.
Edges
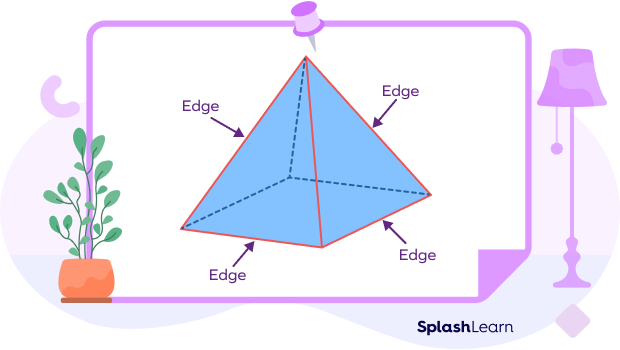
The line segments created by connecting two vertices are referred to as edges. A rectangular pyramid has 8 edges. Of these, 4 edges are the sides of the rectangle located at the base while the other 4 form the sides of the triangles.
Net of a Rectangular Pyramid
The net of a 3D shape is 2D shape formed when it is opened out flat. A net can be folded up to make a 3D shape. The net of a rectangular pyramid has four triangles and one rectangle. The image given below shows the net of the rectangular pyramid.
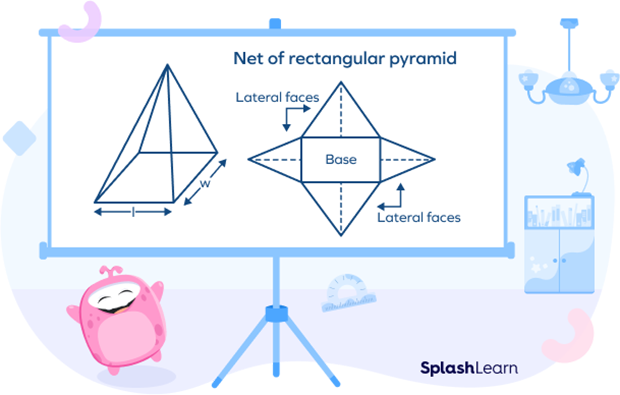
Rectangular Pyramid Types
Depending on the shape of the rectangular pyramid, it is classified into two types. They are as follows:
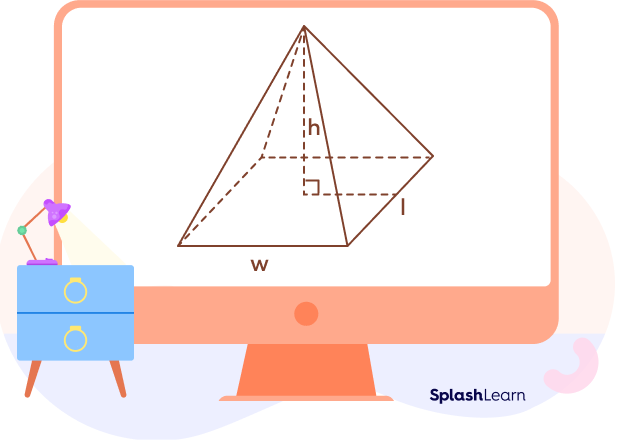
Right Rectangular Pyramid
In the right rectangular pyramid, the apex is directly above the center of the base. It forms a perpendicular to the base, indicating the height of the pyramid.
Oblique Rectangular Pyramid
When the peak or the apex of a rectangular pyramid is not directly above the center of the base, the pyramid is said to be oblique.
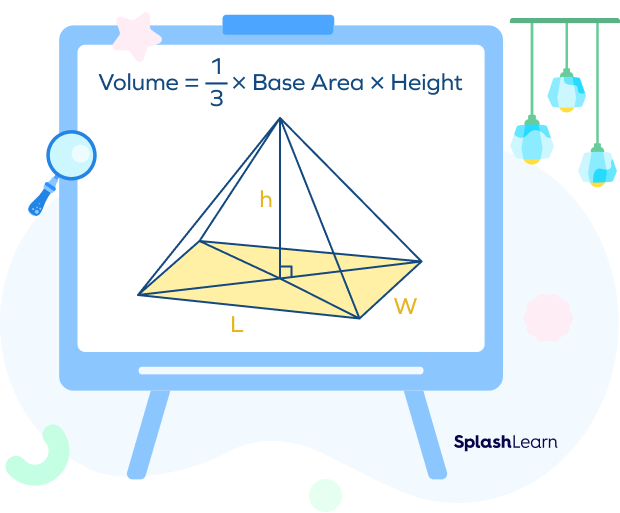
Volume of Rectangular Pyramid
The volume of a 3D figure refers to the space occupied by it. It is measured in cubic units. The formula for the volume of the rectangular pyramid is as follows:
Volume $= \frac{1}{3}\times$ Base Area $\times$ Height
Here,
Base area of the rectangular pyramid $=$ Length$\times$Width
Height is the perpendicular height of the pyramid.
Volume $= \frac{1}{3}\times$ length$\times$width$\times$height
Surface Area of a Rectangular Pyramid
A rectangular pyramid has two types of surface areas: the lateral surface area and the total surface area.
Lateral Surface Area
The lateral surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces. In a rectangular pyramid, the areas of the opposite triangular faces are the same.
Area of front and back triangles
Area of a triangle $= \frac{1}{2} \;base \times height = \frac{1}{2} b \times h$
Area of front triangle $= \frac{1}{2} l \sqrt{(\frac{w}{2})^{2} + h^{2}}$
Area of front triangle $+$ Area of back triangle $= l \sqrt{(\frac{w}{2})^{2} + h^{2}}$
Area of side triangles
The side triangles’ area can be found in a way very similar to that of the front and back triangles, except for that their slant height is $\sqrt{(\frac{l}{2})^{2} + h^{2}}$.
Area of one of the triangles $= \frac{1}{2}w \sqrt{(\frac{l}{2})^{2} + h^{2}}$
Area of two side triangles $= w \sqrt{(\frac{l}{2})^{2} + h^{2}}$
Thus, the lateral surface area of the rectangular pyramid is
LSA $= l \sqrt{(\frac{w}{2})^{2} + h^{2}} + w\sqrt{(\frac{l}{2})^{2} + h^{2}}$
Total Surface Area
To find the total surface area of a rectangular pyramid, we add the area of all the faces (the base and the four lateral faces.
Formula for the Total Surface Area of a Rectangular Pyramid:
TSA $=$ (Area of base) $+$ (Lateral Surface Area)
Area of base $= length \times width = l \times w$
Total Surface Area $=$ (Area of base) $+$ (Lateral Surface Area)
TSA $= (l\times w) + l \sqrt{(\frac{w}{2})^{2} + h^{2}} + w\sqrt{(\frac{l}{2})^{2} + h2}$
TSA $= lw + l \sqrt{(\frac{w}{2})^{2} + h^{2}} + w \sqrt{(\frac{l}{2})^{2} + h^{2}}$ square units.
Facts about Rectangular Pyramid
- The pyramid shape or design is used in different forms of architecture and is observed in industrial scenarios.
- A rectangular pyramid has 5 faces, 5 vertices, and 8 edges.
Conclusion
In this article, we learned in detail about the rectangular pyramid, properties, and different formulas for the rectangular pyramid. Let’s solve some examples and practice problems to understand the concept better.
Solved Examples on Rectangular Pyramid
1. Find the volume of the given pyramid.
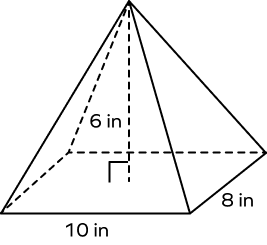
Solution:
Base length $(l ) = 10$ inches
Base width $(w) = 8$ inches
The height of the pyramid $(h) = 6$ inches
The volume of the rectangular pyramid $(V)= (\frac{1}{3}) \times( l \times w \times h)$
$V = (\frac{1}{3}) \times 10 \times 8 \times 6$
$V = (\frac{1}{3}) \times 480$
$V = 160\; in^{3}$
Hence, the volume of the given rectangular pyramid is $160\; in^{3}$.
2. Find the total surface area of a rectangular pyramid if the base length is 12 inches, the base width is 10 inches, and the height of the pyramid is 15 inches.
Solution:
Base length $(l) = 12$ in
Base width $(w) = 10$ in
The height of the pyramid $(h) = 15$ in
Total surface area of a rectangular pyramid TSA $= w\sqrt{h^{2} + (\frac{l}{2})^{2}} + l\;\sqrt{h^{2} + (\frac{w}{2})^{2}} + (l \times w)$
TSA $= (10 \times \sqrt{15^{2} +(\frac{12}{2})^{2}} + 12 \times \sqrt{(15)^{2} +(\frac{10}{2})^{2}} + (12 \times 10)$
TSA $= 10 \times \sqrt{(225 + 36)} + 12 \times \sqrt{(225 + 25)} + 120$
TSA $= 10 \times \sqrt{261} +12 \times \sqrt{250} + 120$
TSA $= 10 \times 16.155 + 12 \times 15.811 + 120$
TSA $= 161.554 + 189.732 + 120$
TSA $= 471.28$ sq. in
Hence, the surface area of the given rectangular pyramid is 471.28 sq. in
3. A rectangular pyramid has a base area of $180\; ft^{2}$ and height of 40 ft. Find the volume.
Solution:
Base Area $= 180\; ft^{2}$
Height $= 40$ ft
We know that,
The volume of the rectangular pyramid $(V)= \frac{1}{3} \times base \; area \times h$
$V = (\frac{1}{3}) \times 180 \times 40$
$V = (\frac{1}{3}) \times 7200$
$V = 2400$ cubic ft.
Hence, the volume of the given rectangular pyramid is 2400 cubic ft.
4. Determine the lateral surface area of a rectangular pyramid if $l = 12$ inches and $w = 8$ inches, and $h= 16$ inches.
Solution:
Base length $(l ) = 12$ inches
Base width $(w) = 8$ inches
The height of the pyramid $(h) = 16$ inches
Lateral surface area of a rectangular pyramid $= l \sqrt{h^{2} + (\frac{w}{2})^{2}} + w\sqrt{h^{2} +(\frac{l}{2})^{2}}$
$= 12 \times \sqrt{16^{2} + (\frac{8}{2})^{2}} + 8 \times \sqrt{16^{2} + (\frac{12}{2})^{2}}$
$= 12 \times \sqrt{256 + 16} + 8 \times \sqrt{256 + 36}$
$= 12 \times \sqrt{272} + 8 \times \sqrt{292}$
$= 12 \times 16.49 + 8 \times 17.08$
$= 197.88 + 136.64$
$= 334.52$ square inches
Hence, the lateral surface area of the given rectangular pyramid is 334.52 sq.in
5. What is the length of the base of a rectangular pyramid if volume $= 144\; yard^{3}$, width $= 6\; yards$, and height $= 9\; yards$?
Solution:
Volume (V) $= 144\; yard^{3}$
Width (w) $= 6\; yards$
Height (h) $= 9\; yards$
We know that,
The volume of the rectangular pyramid $(V) = (\frac{1}{3}) \times (l \times w \times h)$ cubic units
$144 = (\frac{1}{3}) \times (l \times 6 \times 9)$
$432 = (l \times 6 \times 9)$
$432 =(l \times 54)$
$l = \frac{432}{54}$
$l = 8$ yards.
Thus, the length of the base of a rectangular pyramid shaped game room is 8 yards.
Practice Problems on Rectangular Pyramid
Rectangular Pyramid: Definition, Formula, Properties, Examples, FAQs
How many edges does a rectangular pyramid have ?
Rectangular pyramids have 8 edges.
When the peak or the apex of a rectangular pyramid is not directly above the center of the base, the pyramid is said to be _______ .
In the right rectangular pyramid, the apex is directly above the center of the base and in the oblique pyramid the apex is not directly above the center.
A rectangular pyramid has _____ vertices.
Rectangular pyramids have 5 vertices. Of these, 4 vertices are located at the corner of the rectangular base and the top vertex is formed by the intersection of the four edges.
Frequently Asked Questions about Rectangular Pyramids
What is the difference between a pyramid and a prism?
a) Prisms have two congruent or identical bases. Pyramids have only one base.
b) Prisms have rectangular lateral faces. Pyramids have triangular lateral faces.
c) Pyramids have one central vertex, often referred to as an apex or a point where the lateral faces meet, while prisms don’t have a vertex because there are multiple meeting points where the faces connect.
How does the volume of the pyramid change if the type of pyramid changes?
The volume of the pyramid depends on the base area of the pyramid. As the type of pyramid changes, the base of the pyramid changes, thereby changing the base area of the pyramid. This change in the base area of the pyramid changes the volume of the pyramid.
How can we find the surface area of rectangular pyramid with slant height “s”?
Total Surface Area (TSA) $= B + \frac{1}{2}$ Ps
$= (l \times w ) + \frac{1}{2} \times Ps$
Where, $B =$ Base area of the rectangle
$P =$ Base Perimeter
$s =$ Slant height
$l =$ length of the rectangular base
$w =$ width of the rectangular base
How can we find the height of a rectangular pyramid?
We know that the volume of a rectangular pyramid (v) $= \frac{1}{3} \times (l \times w \times h)$
Thus, we can extract the formula for the height of a rectangular-based pyramid using our knowledge of algebra.
Thus, $3V = l \times w \times h$
and $h = \frac{3v}{l \times w}$
How many vertices does a rectangular pyramid have?
A rectangular pyramid has 5 vertices.




















