What Is a Rhomboid in Math?
A rhomboid is a 2D shape. It is a special type of parallelogram in which opposite sides are parallel and equal; and there are no right angles.
A rhomboid is often confused with a rhombus. The key difference is that all sides of a rhombus are equal and opposite sides are parallel, whereas only opposite sides of a rhomboid are equal and parallel.
What does a rhombus look like? What does a rhomboid look like? Have a look!
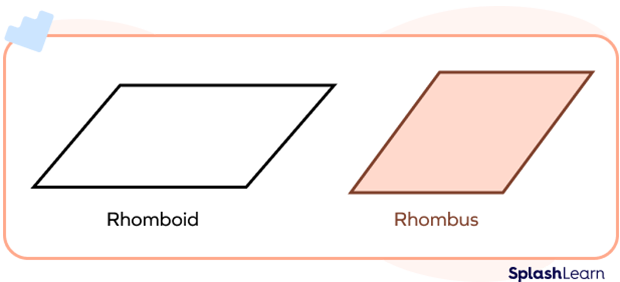
RHOMBOID RHOMBUS
We will discuss the similarities and the differences between the two shapes later in this article.
Rhomboid: Definition
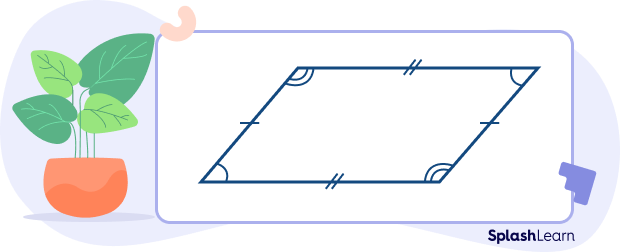
A rhomboid is a type of a parallelogram with no right angles such that the opposite sides are equal and parallel, opposite angles are congruent, and the adjacent sides are not equal.
Properties of Rhomboid
- The opposite sides of a rhomboid are equal and parallel.
- Opposite angles of a rhomboid are congruent.
- A diagonal of a rhomboid divides it into two congruent triangles.
- The sum of the interior angles of a rhomboid is 360 degrees.
- Adjacent angles are not equal and they do not make a right angle.
Note that a rhomboid shape is a special type of a parallelogram, and thus, it inherits all the properties of parallelogram.
Formulas for Rhomboid
Let us now look at some important formulas for rhomboids.
Area of Rhomboid
Simply put, the area of a rhomboid is the space covered by the rhomboid shape. When you cut a rhomboid along its diagonal, you get two congruent triangles with a base and a height. Hence, the area of a rhomboid is twice the area of one triangle.
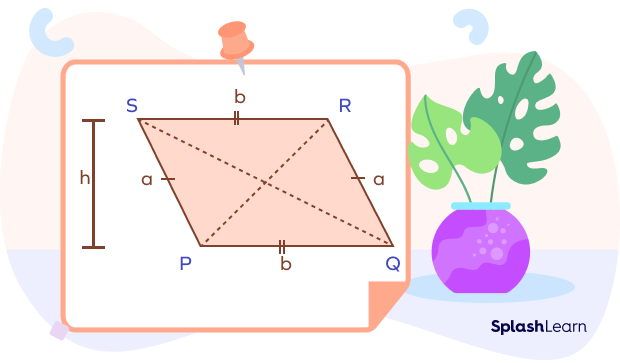
Let’s see how to find the area of a rhomboid. The rhomboid area formula is:
Area of rhomboid $= 2 \times \left(\frac{1}{2} \times base \times height\right) = base \times height = b \times h$
Perimeter of Rhomboid
The perimeter of a rhomboid means the sum of the length of all its four sides, the total length of the outer boundary. The formula for this is as easy as it sounds.
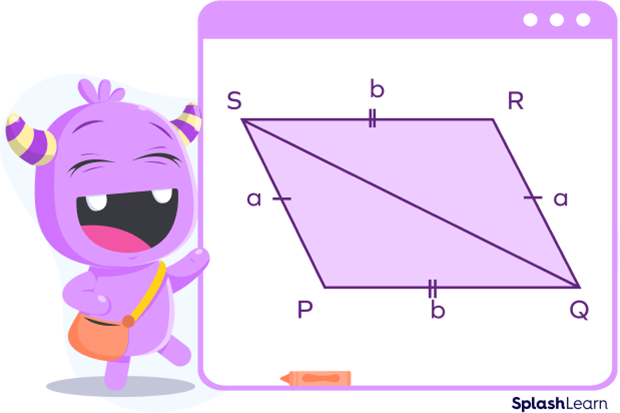
We have already established that the opposite sides of a rhomboid are equal. This means that $PQ = RS = b$ and $RQ = SP = a$
Hence, the perimeter of rhomboid formula is:
Perimeter of rhomboid $= a + a + b + b = 2 (a + b)$
The reason for doubling the sum is that there are two sides of length “a” and two sides of length “b.” Since the perimeter is the sum of all the sides, we get
$a + a + b + b = 2(a + b)$.
Lines of Symmetry in a Rhomboid
Another factor that distinguishes a rhomboid from a rhombus is the lines of symmetry. There are no lines of symmetry in a rhomboid. If you cut out a rhomboid shape from a piece of paper and fold it in half either from any of the sides or along the diagonal, the two parts will not superimpose. Try it out!
However, the rhomboid shape has rotational symmetry of order 2.
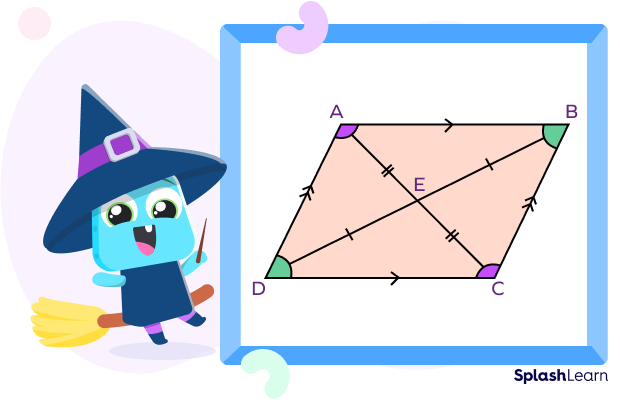
Rhomboid vs. Rhombus
Rhombus and rhomboid are special types of parallelograms.
A rhomboid is a parallelogram in which adjacent sides are not equal and interior angles are not right angles. A parallelogram with all sides of the same length is called a rhombus. Thus, the three shapes are very similar in appearance.
| Rhombus | Rhomboid |
|---|---|
| It is a special case of a parallelogram where all sides are equal and diagonals intersect each other at 90 degrees. | A rhomboid is a parallelogram in which adjacent sides are NOT equal and there are NO right angles. |
| All sides are equal. | Opposite sides are equal. |
| Opposite sides are parallel. | Opposite sides are parallel. |
| Opposite angles are equal. | Opposite angles are equal. |
| Diagonals bisect each other at right angles. | Diagonals do not bisect each other at right angles. |
| Every rhombus is always a rhomboid. | If a rhomboid has all sides equal, it becomes a rhombus. |
Facts about Rhomboid Shape
- A rhomboid is a parallelogram wherein the adjacent sides are not equal and there are no right angles.
- A rhomboid term is also used in biology as humans have two muscles in the upper back, which are known as rhomboid muscles.
Conclusion
In this article, we learned about the rhomboid shape, its properties, formulas, and lines of symmetry. Let’s try our hands at some examples and practice problems.
Solved Examples on Rhomboid Shape
1. What is the area of a rhomboid PQRS when the base is 9 in and the perpendicular height is 7 in?
Solution:
It is given that base, $b = 9$ in and height, $h = 7$ in.
Area of Rhomboid $= base \times height$
Hence, $A = b \times h = 9 \times 7 = 63\; in^2$
2. If the area of a rhomboid is 250 sq. units and the base is 12 units then find its height.
Solution: It is given that area, $A = 250$ sq. units and the base, $b = 12$ units,
We know that the area of a rhomboid, $A = b \times h$
Substituting the values in the equation,
$250 = 12 \times h$
$ h = \frac{250}{12} = 20.84$ units
The perpendicular height of the given rhomboid is 20.84 units.
3. Find the perimeter of a rhomboid whose adjacent sides are 6 units and 9 units long.
Solution:
Side of the rhomboid: $a = 6$ units, and $b = 9$ units.
The perimeter of the rhomboid $= 2(a + b)$
Substituting the values we get,
$P = 2(6 + 9 ) = 30$ units.
Therefore, the perimeter of the rhomboid is 30 units.
4. What is the length of the other side of the rhomboid if its one side is 13.7 inches and the perimeter is 62 inches?
Solution:
It is given that the side of the rhomboid, a = 6 inches and perimeter = 62 inches.
The perimeter of the rhomboid $= 2(a + b)$
Substituting the values we get,
$62 = 2(13.7 + b )$
$13.7 + b = 31$
$b = 31 – 13.7$
$b = 17.3$ inches
5. What is the formula for the area of a rhomboid? Use it to find the area of the given rhomboid shape.
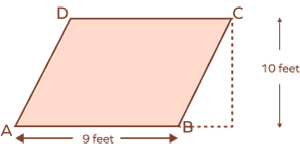
Solution: The area of a rhomboid is given by the formula:
$Area = base \times height = b \times h$
Here, $b = 9$ feet
$h = 10$ feet
$Area = base \times height = 9 \times 10 = 90$ square feet
Practice Problems on Rhomboid Shape
Rhomboid Shape: Definition, Formulas, Properties Examples, Facts
All rhombuses are _______ but not all _________ are rhombuses.
All rhombuses are rhomboids but not all rhomboids are rhombuses.
What is the sum of the interior angles of a rhomboid?
The sum of the interior angles of a rhomboid is 360 degrees.
In a rhomboid ABCD, if $\angle A = 80^\circ$, then $\angle D =$ _____.
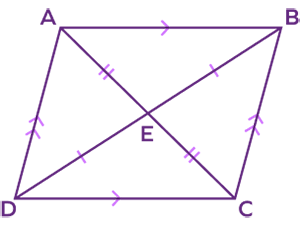
Opposite angles of a rhomboid are equal. So $\angle A = \angle C = 80^\circ$ and also $\angle B = \angle D$
Also, $\angle A + \angle B + \angle C + \angle D = 360^\circ$
$80^\circ + \angle B + 80^\circ + \angle D = 360^\circ$
$160^\circ + \angle B + \angle D = 360^\circ$
$\angle B + \angle D = 200^\circ$ and $\angle B = \angle D$
Therefore, $\angle D = 100^\circ$
The area of a rhomboid ABCD with base is 12.5 cm and perpendicular height 8 cm is
It is given that base, $b = 12.5$ cm and height, $h = 8 cm$.
Area of Rhomboid $= base \times height$.
Hence, $A = b \times h = 12.5 \times 8.= 100\; cm^2$
The adjacent sides of a rhomboid are ________.
The adjacent sides of a rhomboid are not equal.
Frequently Asked Questions on Rhomboid Shape
Is a rhomboid a polygon?
Yes, a rhomboid is a polygon, i.e., a 2D flat shape.
Can we consider every rhomboid a rhombus?
No, every rhomboid is not a rhombus. A rhomboid is a parallelogram where adjacent sides are unequal in length and the angles are not at 90 degrees. Contrary to this, the rhombus has equal sides and the angles are right angles.
What is a parallelogram with right angles called?
A parallelogram with right angles is called a rectangle.
What is the sum of the angles of a rhomboid?
The total of all angles of a rhomboid is $360^\circ$. This is because a rhomboid is a quadrilateral and according to the angle sum property of a quadrilateral, all sides will sum up to $360^\circ$.
How many sides does a rhomboid have?
A rhomboid is a quadrilateral. It has 4 sides.
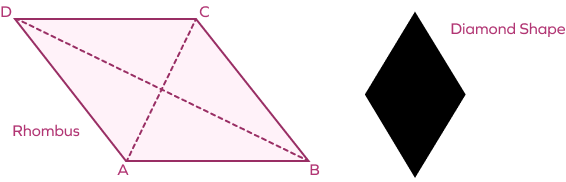
Is a rhombus the same as a diamond shape?
Rhombus resembles a diamond shape, the one in playing cards. A rhombus is more of a geometrical term.