What Are Simple Equations?
Simple equations are mathematical statements that consist of an equal sign (=) and usually contain one variable. These equations are easy to solve and find the value of the variable that makes the equation true.
Example: x + 3 = 7 is a simple equation, where “x” is the variable, and solving it would give “x = 4” as the answer.
Here are some more examples of simple math equations:
3x + 2 = 23
x = 7
2x + 6 = – 4
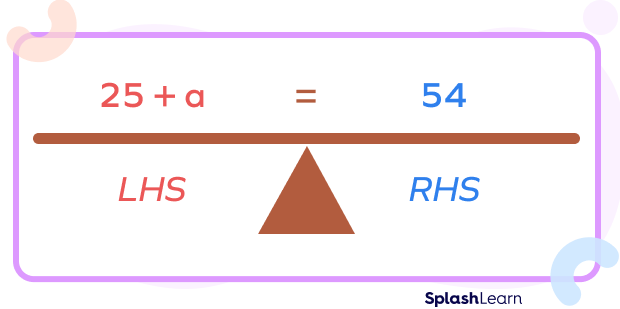
When solving simple math equations, think of the equation as a balance, with the “equal to sign (=)” being the fulcrum or center. Thus, if you do something to one side of the equation, you must do the same thing to the other side. Doing the same thing on both sides of the equation (say, adding, subtracting, multiplying or dividing by any number on each side) keeps the equation balanced.
A simple equation is considered a linear equation in one variable. That means it involves a polynomial of degree one and with one variable only. Solving a simple equation means we find out the value of the unknown variable.
An equation can be compared with a weighing balance with equal weights on both sides. A weighing balance needs to have equal weights on both sides to be perfectly balanced. The same principle will hold in an equality.

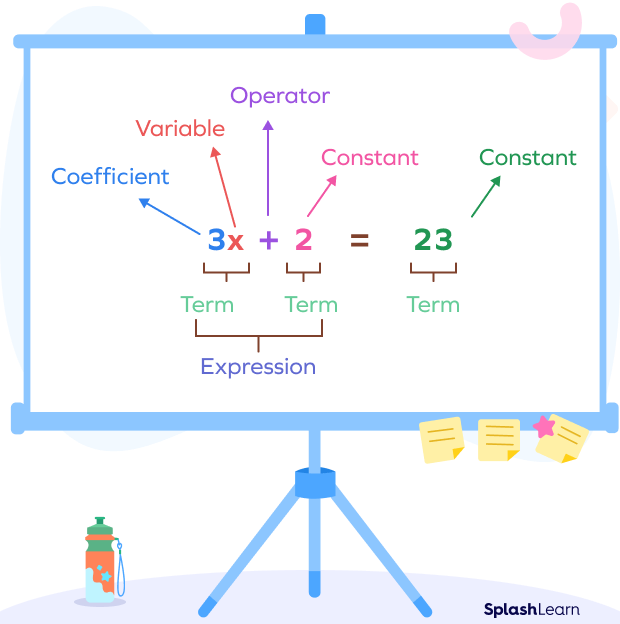
A simple math equation comprises variables and constants. For example, in 3x + 2 = 23, x is a variable. The numbers 2 and 23 are constants, as they do not change. “+” is an operator, the operator may be + or –.
Recommended Games
Methods to Solve Simple Equations
Solving simple equations means to determine the value of x that satisfies the equation. The equation 3x + 2 must equal to 23 once the value has been determined. The equation will hold true even if the Left Hand Side (LHS) is switched out for the Right Hand Side (RHS). The same number can be added, subtracted, multiplied, and divided into each side of a straightforward equation without changing the result.
There are three methods to solve simple equations. They are:
1. Trial and error method
2. Systematic method
3. Transposition Method
Trial and Error method
In a trial and error method, we guess a solution to the equation. We find the values of LHS and RHS of the given equation for different values of the variable. The value of the variable for which
LHS = RHS is the solution of the equation.
Example: x + 6 = 10
LHS = x + 6
RHS = 10
| x | LHS | RHS | Is LHS = RHS ? |
|---|---|---|---|
| 1 | 1 + 6 | 7 | No |
| 2 | 2 + 6 | 8 | No |
| 3 | 3 + 6 | 9 | No |
| 4 | 4 + 6 | 10 | Yes |
Therefore, LHS = RHS for x = 4.
Systematic method/ Balance Method
Keep both sides of the equation balanced by performing the same operations on each side. This maintains the equality between the two sides.
In the systematic method, an equation is compared to a weighing balance. The two sides of an equation are two pans, and the equality sign tells us that two pans are balanced. If equal weights are put in two pans, then two pans will be balanced. If we remove or add equal weights to both the pans, then we can still see the pans are in balance.
Example: x – 5 = 10
Adding 5 on both sides, we get
x – 5 + 5 = 10 + 5
Thus, x = 15
Transposition
The shifting of a number from one side of an equation to another is called “Transposition.”
The transposition method is a technique used to shift numbers from one side of an equation to the other. This involves adding or subtracting the number from both sides while changing its sign. This method uses inverse operations.
For example, if a term has a plus sign on the left-hand side, it becomes a minus sign on the right-hand side and vice versa. Transposition helps in isolating the variable and solving simple equations efficiently.
Let’s see an example to understand this method better.
| Adding or subtracting on both sides(systematic method ) | Transposing |
|---|---|
3x – 10 = 5 Add 10 to both sides. 3x – 10 + 10 = 5 + 10 3x = 5 + 10 3x = 15 | 3x – 10 = 5 Transpose – 10 from LHS to RHS. (On transposing – 10 becomes + 10 ) 3x = 5 + 10 3x = 15 |
Therefore, by using this transposition rule we can find the solution for simple equations.
Recommended Worksheets
Linear Equations
Linear equations are the most common simple equations. A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation.
A linear equation may have more than one variable. A linear equation will make a straight line graph and have a general form of ax + by + c = 0.
Example: 2x + 3y = 4
Applications of Simple Equations
Simple equations can be applied to various situations involving unknowns, making them a valuable tool in real-life problem-solving. Some of the applications of simple equations around us are as follows:
- Scientific and Statistical Fields: Professionals in various scientific and statistical fields use simple equations to calculate totals, percentages, and ratios. This applies to studies in physics, biology, chemistry, astronomy, and other scientific research.
- Financial Applications: Financial professionals, such as accountants and analysts, use simple equations to calculate important financial information like revenue, profits, losses, tax obligations, and return on investments.
- Academic Settings: Simple equations are a part of the math curriculum at different levels. Elementary-level equations involve basic operations and numerical values, while more advanced math, like algebra and trigonometry, deals with complex terms and variables.
- Medical Applications: Medical professionals utilize simple equations to measure and administer medicines and medical components. They rely on equations to assess vital signs and determine medication doses.
- Construction and Engineering: Professionals in the construction industry use geometric formulas and linear equations to design, plan, and implement structural blueprints for buildings and structures.
Simple equations find wide-ranging applications in real-world scenarios, offering valuable tools to professionals across various fields of study.
Facts on Applications of Simple Equations
- For balancing an equation we can (i) add the same number on both the sides, or (ii) subtract the same number from both the sides, or (iii) multiply both sides with the same number, or (iv) divide both the sides by the same number. We make sure that equality remains undisturbed.
- An equation remains the same if the LHS and the RHS are interchanged.
- The value of the variable for which the equation is satisfied is called the solution of the equation.
- Transposing means moving to the other side. Transposition of a number has the same effect as adding the same number to (or subtracting the same number from) both sides of the equation.
Conclusion
In this article, we have learned about simple equations and its applications. You might be surprised to learn that applications of equations turn up in many places besides math classrooms. Knowing how to solve simple equations is a basic math skill used in nearly every academic discipline. Now, let’s solve some easy equation examples and practice problems to understand the concept better.
Solved Examples on Applications of Simple Equations
Example 1: Write the equations for the following statements:
a. Two added to the product of a number and 13 equals 15.
b. Dividing a number by 5 equals 25.
c. The sum of 5 and a number is 11.
Solution:
a. Let the number be x.
The equation is (13 $\times$ x) + 2 = 15
Thus, 13x + 2 = 15
b. Let the number be a.
The equation is $\frac{a}{5}$ = 25
c. Let the number be x.
Sum of 5 and a number = 5 + x
So, the equation is 5 + x = 11
Example 2: Solve equation x + 4 = 10 using the systematic method.
Solution:
In the systematic method we treat LHS and RHS as two pans of a weighing balance.
So, for solving equation x + 4 = 10, we subtract 4 from each side.
x + 4 – 4 = 10 – 4
x = 6
Thus, x = 6
Example 3: If 5 is added to twice a number, the result is 29. Find the number.
Solution:
Let the required number be x.
Converting it into equation, we get
2x + 5 = 29
Solving the equation, we get
2x + 5 = 29
2x = 29 – 5 (Transposing 5 to RHS)
2x = 24
x = 12 (Dividing both sides by 2)
x = 12
Thus, the required number is 12.
Example 4: Total number of the boys and girls in a class is 52. If the number of girls is 10 more than that of boys, find the number of boys?
Solution :
Let us assume the number of boys to be x.
The number of girls will be x + 10.
The total number of boys and girls = x + (x + 10) = x + x + 10 = 2x + 10
It is given that the total number of boys and girls in the class is 52.
Therefore, 2x + 10 = 52
Solving this equation, we get
2x = 52 – 10 (transposing 10 from LHS to RHS)
2x = 42
2x = $\frac{42}{2}$ (transposing 2 from LHS to RHS)
Therefore, x = 21
The number of boys in the class is 21.
Practice Problems on Applications of Simple Equations
Simple equations and Application - Methods, Examples, Facts, FAQs
The solution of the equation x + 3 = 0 is ________.
x + 3 = 0.
Thus, x = - 3
If the LHS and RHS of an equation are interchanged, then ______________.
Changing the position of the LHS and the RHS of an equation does not change the equation
Choose the correct value of the variable which satisfies the following equation. 4n + 17 = 25
Put n = 1, 4 $\times$ 1 + 17 = 25 does not satisfy the equation.
Put n = 2, 4 $\times$ 2 + 17 = 25 satisfies the equation.
The shifting of a number from one side of an equation to another is called __________.
The shifting of a number from one side of an equation to another is called transposition.
In the equation 3x – 3 = 9, transposing – 3 to RHS, we get _________.
In the equation 3x – 3 = 9, transposing that is shifting – 3 to RHS, “- 3” becomes “+ 3”
Thus, 3x = 9 + 3
Frequently Asked Questions about Applications of Simple Equations
How are linear equations used in daily life?
Linear equations are used to find the wages based on hourly pay rate, speed, and medicine dosage based on the patient’s weight.
What is the difference between a simple equation and linear equation ?
A mathematical equation which has mathematical expression on both sides along with at-least one variable and an equal sign ‘=’ is known as a simple equation. For example: 5x + 3x = 8x Whereas a mathematical equation which has mathematical expression on both sides along with two variables and an equal sign ‘=’ is known as linear equation. example: x = 3y + 6.
What is the simplest type of equation?
Linear equations are the most common simple equation and typically consist of one or several terms on either side of an equal sign.
What are constants ?
Constants are a part of the algebraic expression that involve only numbers. They are called constants because the value is always the same. For example: In the expression, 2xy – 4 = 2y; the second term 4 is the constant. 2xy cannot be a constant because the values x and y can be varied, and hence will vary the entire term 2xy.
What is a variable ?
In Math, a variable is an alphabet or term that represents an unknown number or unknown value. They are not constant; the value of these terms can be changed from time to time. For example, in the expression 4y + 3x = 0, the values x and y represent variables. x and y can be any number that satisfies the equation.
What is the main thing to remember when solving simple equations?
The most important thing to remember when solving simple equations is that whatever you do to one side of the equation, you must do to the other side. Using this rule, it is easy to move variables around so that you can isolate them and use basic operations to find their value.




































