Subtracting Polynomials: Definition, Methods, Examples, Steps, FAQs

What Is Subtracting Polynomials?

Subtracting polynomials follows a similar procedure as adding polynomials. We just have to deal with the minus sign $(\;-\;)$ in between.

Consider the expression p$(x)\;-\;q(x)$ representing the subtraction of polynomials. Here, we are subtracting q(x) from p(x). Due to the minus sign before q(x), the signs of all the terms in the polynomial q(x) are changed (“$+$ changes to $-$” and “$-$ changes to $+$”). Next, we simplify by combining the like terms and find the answer.

In simple words, when subtracting polynomials, we reverse the signs of each term in the second polynomial and then add the polynomials as usual.

Let us see how to subtract polynomials.

Methods of Subtracting Polynomials

There are two ways to subtract polynomials:

• Subtracting polynomials horizontally
• Subtracting polynomials vertically

Regardless of which method of subtracting polynomials we use, the idea and the procedure is the same. The only difference is the arrangement or placement of polynomials during the subtraction operation. 

Horizontal Method of Subtracting Polynomials

Take a look at the steps required for the horizontal method of subtracting polynomials with an example.

Example: Subtract $P = 2x^{3} \;-\; 3y^{2} + 3z$ from $Q = 7y^{2} + 5x^{3} \;–\; 2z$.

Here,  $P = 2x^{3} \;-\; 3y^{2} + 3z$ and $Q = 7y^{2} + 5x^{3} \;–\; 2z$

We have to find Q – P.

Step 1: Arrange the two polynomials in the standard forms.

$Q = 7y^{2} + 5x^{3} \;–\; 2z = 5x^{3} + 7y^{2} \;-\; 2z$

$P = 2x^{3} \;-\; 3y^{2} + 3z$ is already in the standard form.

Step 2: Place them horizontally separated by minus sign (–) such that the second polynomial is in the parentheses.

$Q \;-\; P = (5x^{3} + 7y^{2} \;-\; 2z) \;–\; (2x^{3} \;-\; 3y^{2} + 3z)$

Step 3: Remove the parentheses. For the second polynomial, change the sign of each term after removing the parentheses. 

$Q \;-\; P = 5x^{3} + 7y^{2} \;-\; 2z \;–\; (2x^{3} \;-\; 3y^{2} + 3z)$

$Q \;-\; P = 7y^{2} + 5x^{3} \;–\; 2z \;–\; 2x^{3} + 3y^{2} \;-\; 3z$

Step 4: Arrange all like terms together and solve.

$Q \;-\; P = 5x^{3} \;-\; 2x^{3} + 7y^{2} + 3y^{2} \;-\; 2z \;-\;3z$

$Q \;-\; P = 3x^{3} + 10y^{2} \;-\; 5z$ 

Vertical Method of Subtracting Polynomials

In the vertical method, all the equations are arranged in columns according to the like terms. The signs are changed and the operation takes place. 

Take a look at the example of a vertical method of subtracting polynomials given below:

Find: $(7x \;–\; 3y + 6z) \;-\; x \;–\; 4y \;–\; 2z$ using the vertical method.

Step 1: Arrange the two polynomials in the standard form.

Here, both polynomials are already in the standard form.

Step 2: Arrange the expressions one below the other such that the polynomial being subtracted is at the bottom. Align the like terms. There will be two rows, in which the lower row is subtracted from the upper row.

Step 3: Change the signs of all the terms of the second row; positive changes to negative and negative sign changes to positive. Finally, add the like terms.

Facts on Subtracting Polynomials

Conclusion

In this article, we learned to subtract polynomial expressions, different methods to subtract polynomials, facts and examples. Now, let us practice solving problems by subtracting polynomials. 

Solved Examples of Subtracting Polynomials

1. Subtract $2x \;-\; 5y + 3z$ from $5x + 9y \;-\; 2z$  using the horizontal method.

Solution: 

We have to find $(5x + 9y \;–\; 2z) \;-\; (2x \;-\; 5y + 3z)$.

Remove the parentheses by multiply the negative sign with the terms

$= 5x + 9y \;-\; 2z \;–\; 2x + 5y \;-\; 3z$

 Arrange the like terms together.

$= 5x \;–\; 2x + 9y + 5y \;-\; 2z \;-\; 3z$

$= 3x + 14y \;-\; 5z$

2. Subtract $4x \;-\; 10y +15z$ from $5x + 8y \;-\; 20z$ using the horizontal method.

Solution: 

$(4x \;-\; 10y + 15z) \;-\; (5x + 8y \;-\; 20z)$

Sign change of the second polynomial by removing the parentheses and multiplying

$= 4x \;-\; 10y + 15z \;-\; 5x \;-\; 8y + 20z$

 Combine the like terms.

$= 4x \;-\; 5x \;-\; 10y \;-\; 8y + 15z + 20z$

$= \;-\; x \;-\; 18y + 35z$

3.  Subtract $5x \;–\; 3y \;–\; 4z$ from $7x \;–\; 6y + 6z$ using the vertical method.

Solution: 

We have to find $7x \;-\; 6y + 6z \;-\; (5x \;–\; 3y \;–\; 4z)$.

Arrange the expression in two rows with like terms in the same column. Change the sign of each term of the second row and proceed with the operation.

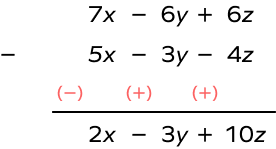
4. Subtract $3a^{3} + 5a^{2} \;–\; 7a + 10$ from $6a^{3} \;-\; 8a^{2} + a + 10$.

Solution: 

$6a^{3} \;-\; 8a^{2} + a + 10 \;-\;(3a^{3} + 5a^{2} \;–\; 7a + 10)$

Arrange the expression in two rows with like terms in the same column. Change the sign of each term of the second row and proceed with the operation.

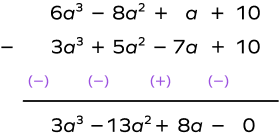
Thus, 

$6a^{3} \;-\; 8a^{2} + a + 10 \;-\; (3a^{3} + 5a^{2} \;–\; 7a + 10)$

$= 3a^{3} \;-\; 13a^{2} + 8a \;-\; 0$

5. Subtract the polynomials horizontally $15x^{3} + 12y^{2} \;-\; 8z \;-\; 7$ from $20x^{3} \;-\; 6y^{2} + 31z + 9$.

Solution:

We have to find $20x^{3} \;-\; 6y^{2} + 31z + 9 \;-\; (15x^{3} + 12y^{2} \;-\; 8z \;-\; 7)$.

 Sign change of the second polynomial through the parentheses

$= 20x^{3} \;-\; 6y^{2} + 31z + 9 \;-\; 15x^{3} \;-\; 12y^{2} + 8z + 7$

 Combine the like terms.

$= 20x^{3} \;-\; 15x^{3} \;-\; 6y^{2} \;-\; 12y^{2} + 31z + 8z + 9 + 7$

$= 5x^{3} \;-\; 18y^{2} + 39z +16$

Practice Problems on Subtracting Polynomials

Frequently Asked Questions about Subtracting Polynomials