What Are Vertical Angles?
Whenever two lines cross or intersect each other, four angles are formed. Out of these, the angles opposite to each other are called vertical angles or vertically opposite angles. Vertical angles are always congruent.
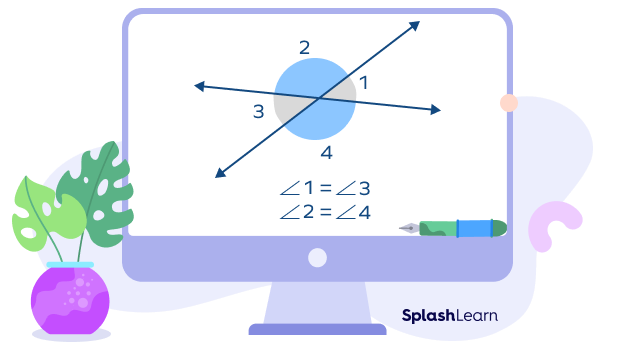
Here, the pairs of vertical angles are
- ∠1 & ∠3
- ∠2 & ∠4
Observe that the two angles opposite to each other are equal.
Recommended Games
Vertical Angles: Definition
Vertical angles can be defined as the angles that lie opposite to each other when two lines intersect.
Two vertical angles always share a common vertex. However, they never share a common side (arm).
For example, ∠AOD and ∠BOC are vertical angles.
They share a common vertex O. However, they do not share a common arm.
Recommended Worksheets
Vertical Angles Theorem
Statement: The vertical angles formed when two lines intersect each other are always equal to each other.
Vertical Angles Theorem: Proof
To prove: Vertical angles formed when two lines intersect each other are congruent.
Here, we have to prove that
∠1 = ∠3
∠2 = ∠4
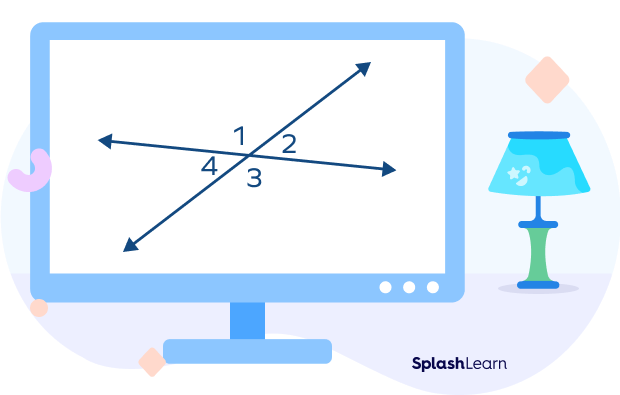
We know that the sum of angles forming a linear pair is 180°.
∠1 +∠2 = 180° (linear pair of angles) ——— (1)
∠1 +∠4 = 180° (linear pair of angles) ——— (2)
From equations (1) and (2), we can see that the RHS is equal.
Equating (1) and (2), we get
∠1 + ∠2 =∠1 +∠4
Thus, ∠2 = ∠4
Similarly, we can prove that ∠1 =∠3
Are Vertical Angles Adjacent?
Vertical angles can never be adjacent. Two adjacent angles share a common vertex and a common arm (or side). Adjacent angles lie next to each other.
On the other hand, the vertical angles lie opposite to each other. They only share a common vertex.
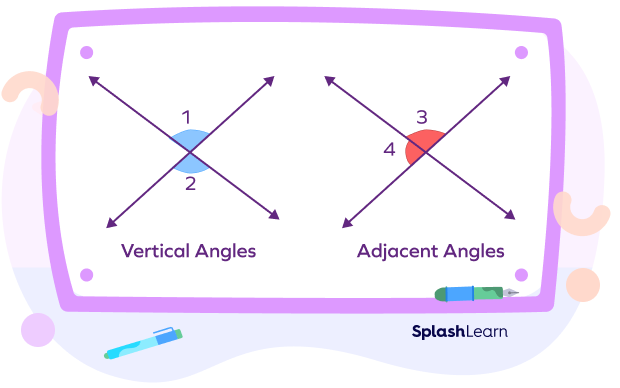
In the above image, we observe that the angles ∠1 and ∠2 are vertical angles and the angles ∠3 and ∠4 are adjacent angles.
Are Vertical Angles Supplementary?
Supplementary angles are the angles which add up to 180°. Vertical angles are supplementary if and only if the lines intersect each other at a 90° angle. In simple words, if the two lines are perpendicular, the vertical angles formed are supplementary.
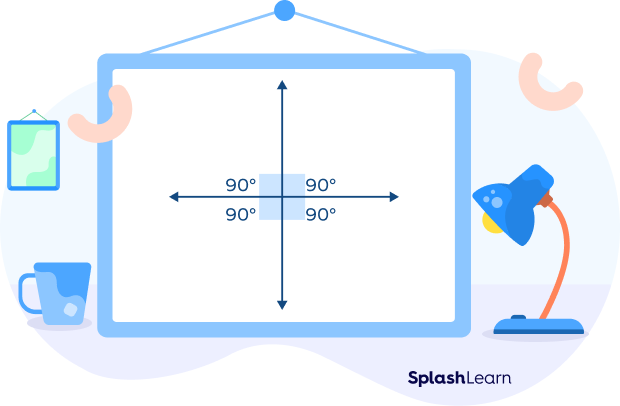
We observe in the above case that all the angles are right angles (equal to 90°).
Thus, the sum of vertical angles will be 90° + 90° = 180°.
Are Vertical Angles Complementary?
We know that vertical angles are always congruent. Complementary angles are the angles that add up to 90°.
Thus, for two vertical angles to be complementary, each of the angles should measure 45°.

When we add both the vertical angle pair, we get
45°+ 45° = 90°.
Using Vertical Angles to Find the Measurement of a Missing Angle
Vertical angles can be very useful when we are given two intersecting lines and we have to find all the missing angles, provided we are given only one angle. Here, we use two important theorems.
- A pair of vertical angles are congruent.
- Angles in a linear pair are supplementary.
Let’s understand this with an example.
Example: Find the angles x, y, and z.
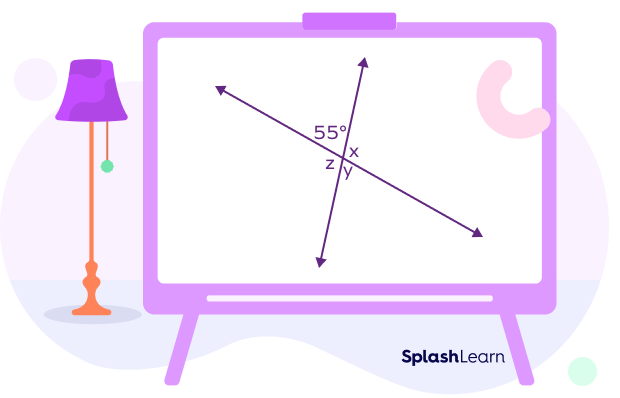
The angle y and the angle measuring 55° are vertical angles. Thus, they are congruent.
We can write
y = 55°
Next, the angle x and y are angles in a linear pair.
Thus, x + y = 180°
x + 55° = 180°
x = 125°
Finally, the angles x and z are vertical angles. Thus, x = z = 125°
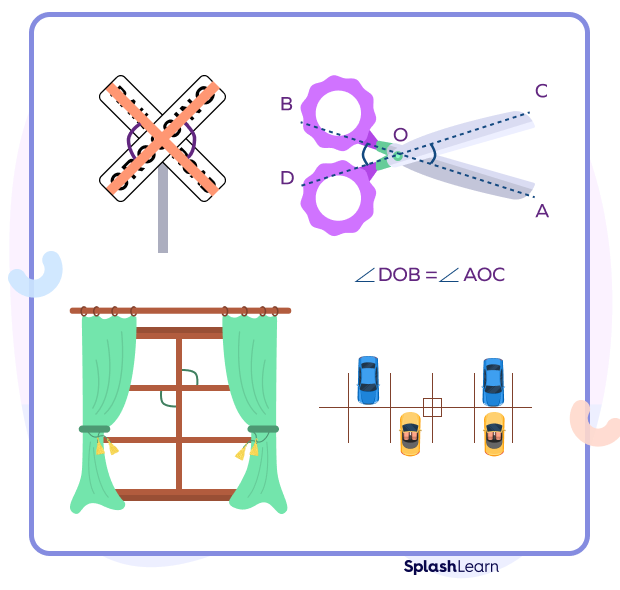
Vertical Angles Around You
You can observe vertical angles in everyday objects around you. Take a look!
Facts about Vertical Angles
Vertical angles can never be adjacent; adjacent angles can never be vertical.
Vertical angles are always congruent.
Conclusion
In this article, we learned about vertical angles and their significance in geometry. Vertical angles are formed by intersecting lines and have equal measures, providing valuable insights into various geometric relationships. Now that we have grasped the concept of vertical angles, let’s take our learning to the next level by putting it into practice. Let’s solve a few examples and tackle some MCQs to solidify our comprehension.
Solved Examples on Vertical Angles
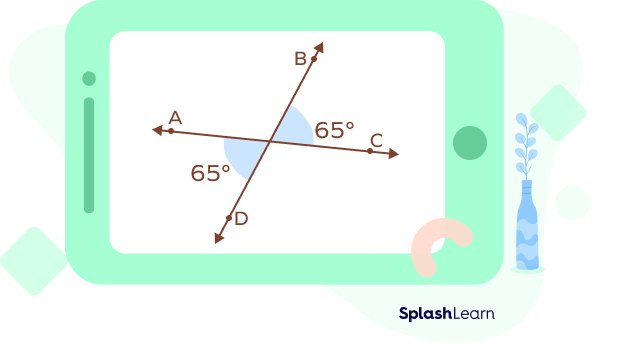
1. Find the measure of ∠DCE. Also, find the other missing angles.
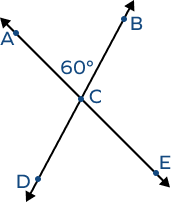
Solution:
∠DCE and ∠ACB are vertical angles.
Vertically opposite angles are always equal.
Thus, ∠DCE = ∠ACB = 65°
Here, ∠ACB and ∠BCE are angles in a linear pair.
∠ACB + ∠BCE = 180°
60° + ∠BCE = 180°
∠BCE = 120°
Also, ∠BCE and ∠ACD are vertical angles.
Thus, ∠BCE = ∠ACD = 120°
2. Identify the vertical angles.
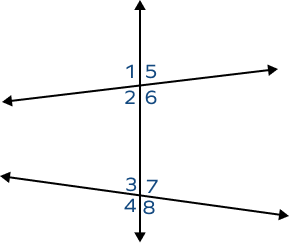
Solution:
Vertical angles can be defined as the angles that lie opposite to each other when two lines intersect.
Pairs of vertical angles in the above diagram are:
- ∠1, ∠6
- ∠2, ∠5
- ∠3, ∠8
- ∠4, ∠7
3. If ∠p = 35°, find m∠q.
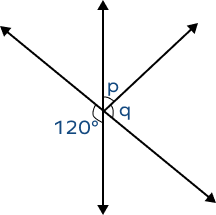
Solution:
From the figure, we can observe that the angle 120° and the angle formed by combining p and q are vertically opposite.
Thus, ∠p + ∠q = 120°.
35°+∠q = 120°
∠q = 120° – 35°
∠q = 85°
4. Are the angles ∠AOB and ∠COD vertical angles? Can we say that∠AOB=28°?
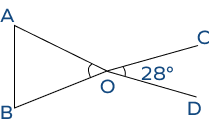
Solution:
Vertical angles are formed when two straight lines intersect each other.
In the diagram, you can see that line BO and line OC are two different lines.
The angles ∠AOB and ∠COD are not formed by the intersection of two straight lines. Thus, the angles are not vertical.
Hence, ∠AOB ≠ 28°.
Practice Problems on Vertical Angles
Vertical Angles - Definition, Theorem, Facts, Examples
Observe the diagram and choose the correct statement.
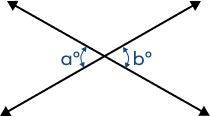
Angles a and b are vertical angles. Vertically opposite angles are always equal.
So, a = b
Vertical angles are always ________.
Vertical angles are always congruent.
What is the value of x?
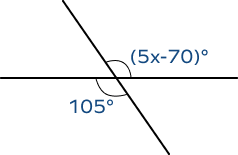
(5x – 70)° = 105° …(vertically opposite angles)
5x = 175°
x = 35°
Vertical angles formed are supplementary when the two lines are ____.
If the two lines are perpendicular, the vertical angles formed are supplementary.
If two vertical angles are complementary, then each angle measures
If two vertical angles are complementary, then each angle measures 45°.
45° + 45° = 90°
Frequently Asked Questions on Vertical Angles
What does it mean when vertical angles measure 90°?
If vertical angles measure 90°, it means that the lines forming them are perpendicular.
Are vertical angles always congruent?
Yes, vertical angles are always congruent.
What is meant by interior and exterior angles?
The angles that are formed inside of a shape by the sides are known as the interior angles, whereas the angles formed on the outside of the shape are known as the exterior angles.
Why are vertical angles always congruent?
Vertical angles are always congruent due to their position; they are formed by the intersection of two lines, creating opposite angles with equal measures. This geometric property is a result of the angles sharing a common vertex and being on opposite sides of the intersecting lines, leading to their equal measures.




































