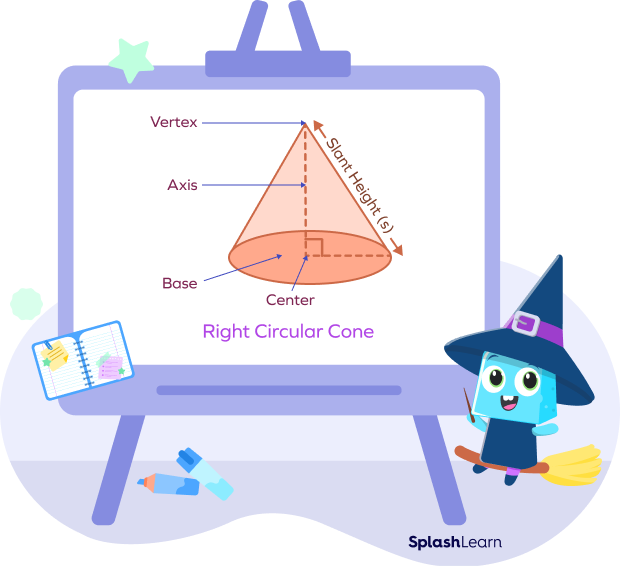
What Is the Volume of a Right Circular Cone?
The volume of a right circular cone is the total space occupied by the right circular cone. It is equal to one-third the product of the base area and height.
The formula to find the volume of a right circular cone is $V = \frac{1}{3} \pi r^{2}h$, where r is the radius of the base circle and h is the height of the cone.
A right circular cone is a type of cone in which the axis of the cone is the line joining the vertex (apex) and the midpoint of the circular base. A right circular cone is generated by a revolving right triangle about one of its legs.
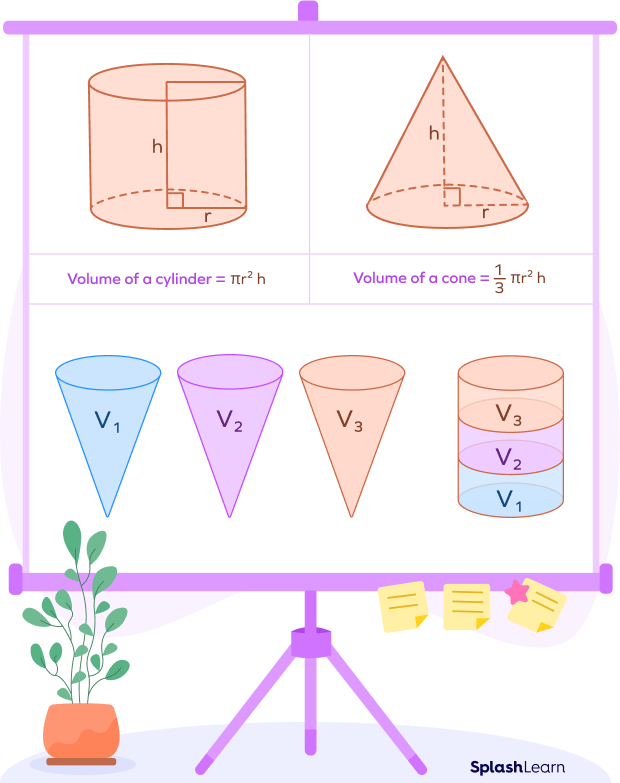
We know that the volume of a cylinder is given by $\pi r^{2}h$, where r is the radius and h is the height. Thus, we can say that the volume of a cylinder is three times that of a cone having the same radius and height. Three such cones can fill up the cylinder.
Recommended Games
Volume of Right Circular Cone Formula
Volume of a right circular cone $= \frac{1}{3} \pi r^{2}h$
where
r = radius of the circular base
h = height of the cone
Recommended Worksheets
How to Find the Volume of a Right Circular Cone
Let’s understand how to calculate the volume of a right circular cone based on the provided information.
Finding Volume Using Radius and Slant Height of a Cone
If we know the radius and slant height of the cone, we will first find the height using the
formula: $h = \sqrt{l^{2}\;-\;r^{2}}$
Once we know the height, we can calculate the volume as
Volume of the cone $= \frac{1}{3} r^{2} h = \frac{1}{3} \pi r^{2}\sqrt{l^{2}\;-\;r^{2}}$.
This is the formula for the volume of a right circular cone with slant height.
Finding Volume Using Height and Slant Height of a Cone
If we know the height and slant height of the cone, we will first find the radius using the formula:
$r = \sqrt{l^{2}\;-\;h^{2}}$
Once we know the radius, we can calculate the volume as
Volume of the cone $= \frac{1}{3} \pi r^{2}h$
Facts about Volume of a Right Circular Cone
- The volume of a right circular cone is exactly one-third of the volume of a cylinder with the same base radius and height.
- If we keep the height constant, a cone with a larger base area will have a larger volume, while a cone with a smaller base area will have a smaller volume.
Conclusion
In this article, we learned how to find the volume of a right circular cone, its formula, and different ways of calculating it. Let’s use the formula to solve a few problems and objective questions based on the concept of volume of a right circular cone.
Solved Examples on Volume of a Right Circular Cone
1. A cylinder and a cone have the same radius and same height. If the volume of a cylinder is 1037 cubic inches, what is the volume of the cone?
Solution:
Volume of cone $= \frac{1}{3}\times$ Volume of cylinder
Volume of cone $= \frac{1}{3} \times 1038$
Volume of cone = 346 cubic inches.
2. Find the volume of the right circular cone if the radius is 7 units and height is 9 units.
Solution:
Radius of the cone (r) = 7 units
Height of the cone (h) = 9 units
Volume $= \frac{1}{3} \pi r^{2} h$
Volume $= \frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 9$
Volume = 462 cubic units.
3. What is the volume of a conical tent whose radius is 14 feet and height is 12 feet?
Solution:
Radius of the conical tent (r) = 14 feet
Height of the conical tent (h) = 12 feet
Volume of the cone $= \frac{1}{3} \pi r^{2}h$
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times 14 \times 12$
$V = 2464$ cubic feet.
4. If the volume of the right circular cone is 24.5π cubic inches and height is 6 inches, then what will be the radius of the cone?
Solution:
Volume of the cone = 24.5π cubic inches
Height of the cone (h) = 6 inches
$\frac{1}{3} \pi r^{2} h = 24.5$
$\frac{1}{3} r^{2} \times 6 = 24.5$
$2r^{2} = 24.5$
$r^{2} = \frac{24.5}{2} = 12.25$
r = 3.5 inches
5. The volume of the right circular cone is 980 cubic inches. What is the height of the cone if the base radius is 7 inches?
Solution:
Volume of the cone = 980 cubic inches
Radius of the cone (r)=7 inches
$\frac{1}{3} \pi r^{2} h = 980$
$\frac{1}{3} \times 7 \times 7 \times h = 980$
$\frac{49h}{3} = 980$
$h = \frac{980 \times 3}{49} = 60$ inches
Practice Problems on Volume of a Right Circular Cone
Volume of a Right Circular Cone – Definition, Formula, Examples
The slant height of the right circular cone is 13 inches and radius is 5 inches. What is the height of the cone?
Radius (r) = 5 inches
Slant height (l) = 13 inches
$h = \sqrt{l^{2}\;-\;r^{2}}$
$h = \sqrt{13^{2}\;-\;5^{2}} = \sqrt{169\;-\;25} = \sqrt{144} = 12$ inches
Find the volume of a right circular cone in terms of radius if radius is equal to the height.
Let radius of the cone be r units and height of the cone be h units.
Given: r = h
Volume of the cone $= \frac{1}{3} \pi r^{2} r = \frac{1}{3} \pi r^{3}$
If the height of the cone is 18 inches and base diameter is 14 inches, then what will be the volume of the cone?
Base diameter of the cone (d)=14 inches
Base radius of the cone (r)=7 inches
Height of the cone (h)=18 inches
Volume of the cone $= \frac{1}{3} \pi r^{2} h$
$= \frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 18 = 924$ cubic inches.
If the volume of the cone is 100 cubic units, and height is 12 units, then what will be the lateral height?
Volume of the cone $= 100\pi$ cubic units
Height of the cone (h) = 12 units
$\frac{1}{3} r^{2} h = 100\pi$
$\frac{1}{3} \times r^{2} \times 12 =100$
$4r^{2} = 100$
$r^{2} = \frac{100}{4} = 25$
$r = 5$ units
$l = \sqrt{r^{2} + h^{2}}$
$l = \sqrt{5^{2} + 12^{2}} = \sqrt{25 + 144}$
$l = \sqrt{169} = 13$units
What is the volume of the right cone for the given radius 6 inches and height 14 inches? $( \pi = 3.14)$
Base radius of the cone (r) = 6 inches
Height of the cone (h) = 14 inches
Volume of the cone $= \frac{1}{3} \pi r^{2} h$
$V =\frac{1}{3} \times 3.14 \times 6 \times 6 \times 14 = 527.52$ cubic inches.
Frequently Asked Questions about Volume of a Right Circular Cone
What is the formula for curved surface area of a right circular cone?
The formula for curved surface area of a right circular cone is $\pi r l$, where r is the radius of the base and l is the slant height.
What is the total surface area of a right circular cone?
The formula for total surface area of a right circular cone is $\pi r l + r^{2} = r(l + r)$ where r is the radius of the base and l is the slant height.
What is an oblique circular cone?
If the axis is not perpendicular to the base, the cone is called an oblique circular cone. In the oblique cone, the apex is not aligned with the center of the circular base
If the radius and height of a right circular cone gets doubled, will the volume get doubled?
Original volume $= \frac{1}{3} \pi r^{2} h$
New Volume $= \frac{1}{3} \times (2r)^{2} \times (2h) = 8 \times \frac{1}{3} \pi r^{2}h = 8$ times original volume
The volume gets 8 times the original volume.
How to find the volume of a layer of a right circular cone?
To find the volume of a layer within a right circular cone, use the formula for the volume of a cone $(V = \frac{1}{3} \pi r^{2} h)$, where h and r represent the height and radius of the layer.



























