What are Inverse Operations?
Inverse means the opposite. So in math, an inverse operation can be defined as the operation that undoes what was done by the previous operation. The set of two opposite operations is called inverse operations.
For example: If we add 5 and 2 pens, we get 7 pens. Now subtract 7 pens and 2 pens and we get 5 back. Here, addition and subtraction are inverse operations.

Recommended Games
What Are Operations?
A mathematical “operation” refers to calculating a value using operands and a math operator. The numbers used for an operation are called operands. Based on the type of operation, different terms are assigned to the operands. Operators are the symbols indicating a math operation, for example:
- + for addition
- − for subtraction
- × for multiplication
- ÷ for division
- = for equal to, indicates the equality, that is, the left hand side value is equal to the right hand side value.
Examples of inverse operations are given below:
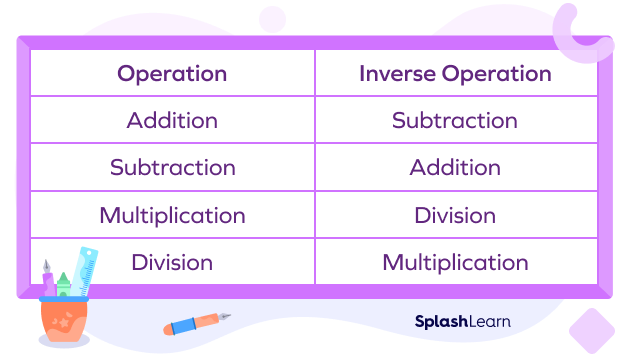
Recommended Worksheets
Addition and Subtraction
Addition and subtraction are inverse operations, which means addition undoes subtraction and subtraction undoes addition. We can rearrange the numbers given in the addition equation and then we can use the addition equation to get two different subtraction equations.
For example: $15 + 6 = 21$
The two subtraction equations formed are: $21$ $–$ $6 = 15$ and $21$ $–$ $15 = 6$
We can even show after this that when you take a number for example 15, add and subtract the same number to 15, we get 15 again.
i.e., $15 + 6 \;–\; 6 = 15$
Similarly, we can rearrange the numbers that are given in the subtraction equation and then we can make two addition equations.
For example: $30$ $–$ $14 = 16$
The addition equations formed are: $14 + 16 = 30$ and $16 + 14 = 30$
When we add a number and subtract the same number later on, the effect is reversed.
$16 \;–\; 4 + 4 = 16$
Multiplication and Division
Multiplication and division are the inverse operations, which means multiplication undoes division and division undoes multiplication. We can rearrange the numbers given in the multiplication equation and then we can do two different division equations.
For example: $7 \times 4 = 28$
The two division equations formed are: $28\div4=7$ and $28\div7=4$
Also, when we multiply a number and then divide the same number later on, the effect is reversed.
$12\times4=48; 48\div4=12$
Similarly, we can rearrange the numbers that are given in the division equation and then we can make two multiplication equations.
For example: $45\div9=5$
The multiplication equations formed are: $9 \times 5 = 45$ and $5 \times 9 = 45$
Also, when we divide a number and then multiply the same number later on, the effect is reversed.
$12 \div 4 = 3; 3 \times 4 = 12$
Properties of Inverse Operations
- Inverse Additive Property
The value, which, when added to the original number gives 0, is known as the additive inverse.
Suppose, x is the original number, then its additive inverse will be minus of x, i.e., $-$$\text{x}$, such that:
$\text{x + ( – x ) = x – x} = 0$
For example, $6+( $ $-$ $ 6)=0$. Hence, $–6$ is the additive inverse of 6 and vice versa.
Suppose, $-$$\text{x}$ is the original number, then its additive inverse will be the positive value of x, i.e., x.
- Inverse Multiplication Property
The value, which, when multiplied to the original number gives 1, is known as the multiplicative inverse.
Suppose, x is the original number, then its multiplicative inverse will be the reciprocal of $\text{x}$, i.e.,$\frac{1}{\text{x}}$, such that:
$\text{x}\times\frac{1}{\text{x}}=1$
For example, $6\times\frac{1}{6}=1$. Hence, $\frac{1}{6}$ is the multiplicative inverse of 6 and vice versa.
Suppose, $\frac{1}{x}$ is the original number, then its multiplicative inverse will be reciprocal of $\frac{1}{x}$, i.e., $x$.
For example: multiplicative inverse of $\frac{3}{4}$ is $\frac{4}{3}$.
Solved Examples on Inverse Operations
Example 1: Form the subtraction equations from $24 + 13 = 37$.
Solution: $37$ $–$ $24 = 13$ and $37$ $-$ $13 = 24$
2. What is the additive inverse of –10?
Solution: Since –10 is a negative number, its additive inverse will be a positive number. So, the additive inverse of –10 will be 10.
3. What is the multiplicative inverse of $(3-\frac{1}{4})$?
Answer: $(3-\frac{1}{4})=\frac{12-1}{4}=\frac{11}{4}$
Multiplicative inverse of $\frac{11}{4}$ is $\frac{4}{11}$.
Practice Problems on Inverse Operations
Inverse Operations - Definition with Examples
If $15$ $-$ $12=3$, what will be the addition equation?
The addition equation for $15$ $-$ $12 = 3$ is $12 + 3 = 15$.
If $34=12$, what will be the division equation?
The division equations will be $12\div3=4$ and $12\div4=3$.
What will be the additive inverse of $3\times6$?
$3\times6=18$. Additive inverse of 18 is $-$ $18$.
Frequently Asked Questions on Inverse Operations
What is the inverse operation for the square of the number?
The inverse operation for the square of a number is the square root. If $8^2=64$, then $\sqrt{64}=8$.
What is the purpose of inverse operation?
Inverse operations are used to reverse the effect of one operation on the other. The purpose of inverse operations is to understand the relation between the basic math operators $+$, $−$, $\times$, $\div$ so that solving an equation becomes easier and time saving.
How is inverse operation used in solving the equations?
The inverse operations are used in solving the equations for isolating the variables by applying inverse operations on both the sides.




































