Additive Inverse: Definition, Formula, Properties, Facts, Examples

What Is the Additive Inverse of a Number?

Additive inverse of a number is a number that, when added to the original number, gives the sum of 0. In simple words, the sum of a number and its additive inverse is always 0.

Mathematically, the additive inverse of a real number n is denoted as – n. 

Similarly, the additive inverse of – n is n.

n + ( – n) = 0 for every real number n.

In simple words, the additive inverse of a number is the opposite or negative of that number. In general, we can study the concept of additive inverse for integers, rational numbers, real numbers, etc. Note that the number 0 is known as the additive identity.

Additive inverse examples:

• The additive inverse of 7 is – 7, since 7 + (– 7) = 0.
• ​​The additive inverse of –10 is 10.
• The additive inverse of – 99 is 99, since (– 99) +99 = 0.
• The additive inverse of 0 is 0 itself, because 0 + 0 = 0.

Additive Inverse Definition

The additive inverse of a number is the number that, when added to the given number, results in the sum of 0.

The additive inverse of a number is also called the opposite or the negation (or negative) of that number.

Additive Inverse Property

If the sum of two real numbers is zero, then each real number is said to be the additive inverse of the other.

In simple words, if a + b = 0, where a and b are real numbers, then we can say that

• a is the additive inverse of b, and
• b is the additive inverse of a.

Additive Inverse on a Number Line

On a number line, we can easily find the additive inverse of a number. Note down the distance of the given number from the origin. Now, mark the point to the opposite direction of 0, which lies at the same distance. 

In other words, 0 is the midpoint of the line segment joining the given number and its additive inverse on a number line.

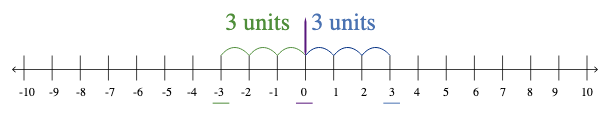
Additive Inverse Formula

Additive inverse of x  = 0 – x

Additive inverse of x  = ( – 1) $×$ x

How to Find the Additive Inverse of a Number

We can find the additive inverse of a number using different methods.

Formula 1: Subtraction method

Let x be any real number. To find the additive inverse of x, simply subtract x from 0.

Additive inverse of x  = 0 – x

Examples: 

Additive inverse of 6 = 0 – 6 = – 6

Additive inverse of – 9 = 0 – ( – 9) = 9

Formula 2: Multiplication method

Let x be any real number. To find the additive inverse of x, simply multiply x with –1.

Additive inverse of x  = (– 1) $×$ x

Examples:

Additive inverse of 1 = ( –1 ) $×$ 1 = – 1

Additive inverse of – 78 = (– 1) × (– 78) = 78

Additive Inverse: Properties

• – ( – x) = x
• – (x + y) = – x – y
• –(x – y) = y – x
• – ($\frac{x}{y}$)= $\frac{x}{– y}$
• $– (\frac{– x}{y})= \frac{x}{y}$
• – (x + y)] = (– x) + (– y)
• – (x – y) = ( – x) + y
• (– x) $\times$(– y)= x y
• x $\times$ (– y) = (– x) y =– (x $\times$ y)

Additive Inverse of Different Numbers

Additive inverse of natural numbers and whole numbers

Natural numbers are counting numbers, defined by the set {1, 2, 3, 4, 5, 6, … }. 

Whole numbers are the set of natural numbers with 0 or {0, 1, 2, 3, 4, 5, …).

Natural numbers are positive. Whole numbers (except 0) are also positive. Thus, the additive inverse of any natural numbers or a whole number (except 0) is always negative.

Examples: 

• Additive inverse of 0 is 0.
• Additive inverse of 1 is -1.
• Additive inverse of 5783 is -5783.
• Additive inverse of 49 is -49.

Additive inverse of integers

The set of integers consists of positive integers, negative integers, and 0.

Integers = {…,-3,-2,-1, 0, 1, 2, 3, …}

The additive inverse of negative integers is always positive.

The additive inverse of positive integers is always negative.

Additive inverse of 0 is 0.

Examples: 

• The additive inverse of -10 is -(-10) = 10.
• The additive inverse of 42 is -(42) = -42.
• The additive inverse of -42 is 42.

Additive Inverse of Fractions

A fraction is a number represented as $\frac{x}{y}$, where x and y are whole numbers, and y is not equal to 0.

The additive inverse of a fraction $\frac{x}{y}$ is $\frac{-x}{y}$.

Examples: 

• Additive inverse of $\frac{7}{8}$ is $\frac{-7}{8}$.
• Additive inverse of $\frac{6}{7}$ is $\frac{-6}{7}$.

Additive Inverse of Rational Numbers

Rational numbers are of the form $\frac{p}{q}$, where p and q are integers, and q is not equal to 0.

The additive inverse of a rational number $\frac{p}{q}$ is $\frac{-p}{q}$.

Examples: 

• Additive inverse of $\frac{5}{9}$ is $\frac{-5}{9}$.
• Additive inverse of $\frac{-1}{7}$ is $\frac{1}{7}$.

Additive inverse of Decimals

For any decimal x, its additive inverse is -x. 

For instance, the additive inverse of 0.25 is -0.25, as 0.25 + (- 0.25) = 0.

Additive Inverse and Multiplicative Inverse

Additive Inverse	Multiplicative Inverse
Additive inverse is a number that, when added to the original number, the sum is 0.	Multiplicative inverse is a number that, when multiplied with the original number, the product is 1.
The additive inverse of a number is the negative or opposite of that number.	The multiplicative inverse of a number is the reciprocal of that number.
The sum of a number and its additive inverse is always 0.	The product of a number and its multiplicative inverse is always 1.
Additive inverse of 0 is 0.	0 does not have a multiplicative inverse.
For any real number n, its additive inverse is -n.	For any non-zero real number n, its additive multiplicative inverse is $\frac{1}{n}$.

Facts about Additive Inverse

Conclusion

In this article, we learned about the concept of additive inverses and how they play a crucial role in mathematics. Understanding the additive inverse allows us to work with negative numbers more effectively and solve a variety of mathematical problems. Let’s solidify our understanding by practicing a few examples and attempting MCQs for better comprehension.

Solved Examples on Additive Inverse

1. What is the additive inverse of 12345?

Solution: 

Given number = 12345 

Additive inverse of 12345 = 0 – 12345 = -12345

2. What is the additive inverse of $\frac{-10}{13}$?

Solution: 

The additive inverse of $\frac{x}{y}$ is $\frac{-x}{y}$.

Additive inverse of $\frac{-10}{13} = \;-\; (\frac{-10}{13}) = \frac{10}{13}$

Thus, the additive inverse of $\frac{-10}{13}$ is $\frac{10}{13}$.

3. The additive inverse of a number is -6. Find the number.

Solution:

Let x be the number.

Additive inverse of x = -x

It is given that the additive inverse is -6.

 Thus, – x = -6

x = 6

The required number is 6.

4. Is 3x + 5 additive inverse of – 3x – 5?

Solution:

The sum of a number and its additive inverse is 0. 

Let’s find the sum of 3x + 5 and – 3x – 5.

(3x + 5) + (- 3x – 5)= 3x + 5 – 3x – 5 = 0 

So, 3x + 5 is the additive inverse of -3x – 5.

Practice Problems on Additive Inverse

Frequently Asked Questions on Additive Identity