Area of Parallelogram – Formula, Vector Form, Facts, Examples, FAQs

What Is the Area of Parallelogram?

The area of a parallelogram is defined as the measure of the two-dimensional space enclosed within its boundaries. It is calculated by multiplying the length of the base by its height, which is the perpendicular distance between the base and the opposite side.

A parallelogram is a special quadrilateral in which opposite sides are parallel and equal in length. 

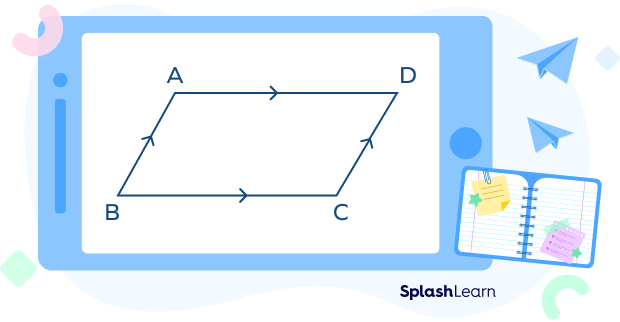
The given figure shows a parallelogram ABCD. 

AB II CD and AB = CD.

AD II BC and AD = BC.

Area of a parallelogram = Base $\times$ Height

You might be wondering if this is the same formula that we use to calculate the area of a rectangle. That’s true!

The formulas for the area of a parallelogram and a rectangle are the same because any parallelogram can be transformed into a rectangle with the same base and height. Try to visualize it with the help of the given diagram!

Since the base and height of the parallelogram remain the same in this transformation, the area of the parallelogram is equal to the area of the resulting rectangle.

Area of Parallelogram: Formula

The area of a parallelogram can be calculated using the formula:

Area = base $\times$ height

The base refers to the length of base of the parallelogram. We can choose any of the four sides of a parallelogram as the base. 

The height is the perpendicular distance between the base and the opposite parallel side. It’s important to note that the height must be measured perpendicular to the base we choose.

Let’s say the base of the parallelogram is represented by ‘b‘ units and the height by ‘h‘ units. 

The formula for the area of the parallelogram can be written as:

Area = b $\times$ h

The area of a parallelogram is expressed in square units. For example, if the base and height are measured in inches, the area will be in square inches $(in^{2})$.

How to Find the Area of a Parallelogram

The area of a parallelogram can be calculated in the following cases:

1. When the base and height are known.

2. When the angle between the adjacent sides and their lengths are known.

3. When the two diagonals and any of the angles at which they intersect are known.

Finding Area of Parallelogram Using Base and Height

Let’s say the base of the parallelogram is represented by ‘b‘ units and the height by ‘h‘ units. 

The formula for the area of the parallelogram can be written as:

Area = base $\times$ height

Area = b $\times$ h (square units)

Example: In a parallelogram, if the base is 11 units and the height is 6 units, what is the area?

Solution: 

Base of the parallelogram = 11 units

Height of the parallelogram = 6 units

Area of parallelogram = b $\times$ h = 11 $\times$ 6 = 66 square units of 66 $unit^{2}$

Finding Area of Parallelogram Using Lengths of Sides

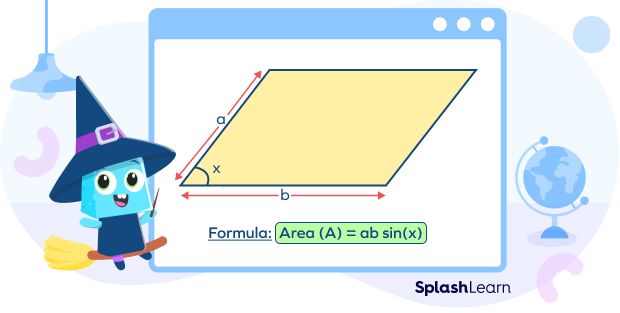
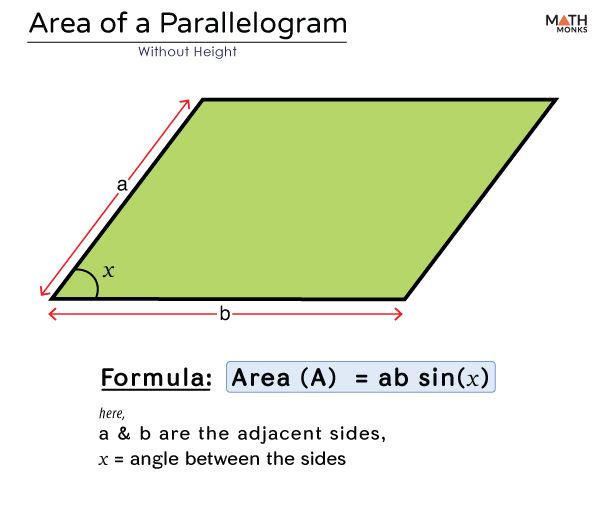
The area of the parallelogram can also be calculated without height. Let the lengths of adjacent sides be ‘a’ units and ‘b’ units, and θ be the angle between them. 

Area of parallelogram = a $\times$ b $\times$ sin(θ)

where ‘a’ and ‘b’ are the lengths of the adjacent sides, 

θ is the angle between them.

This formula is derived from the fact that a parallelogram can be divided into two congruent triangles. By using the trigonometric relationship between the sides and angles of a triangle, we can calculate the area of each triangle and then sum them up to find the total area of the parallelogram.

Example: In a parallelogram, the lengths of the adjacent sides are 5 units and 8 units, and the angle between them is 60 degrees. Find the area of the parallelogram.

Solution:

a = 5 units, b = 8 units, θ = 60 degrees

Using the formula for the area of a parallelogram with adjacent sides and the angle between them:

Area = a $\times$ b $\times$ sin(θ)

Area =  5 $\times$ 8 $\times$ sin(60º)

Area = 40 $\times \frac{\sqrt{3}}{2}$

Area = $20\sqrt{3}$ square units

Therefore, the area of the parallelogram is $20\sqrt{3}$ square units.

Finding Area of Parallelogram Using Diagonals

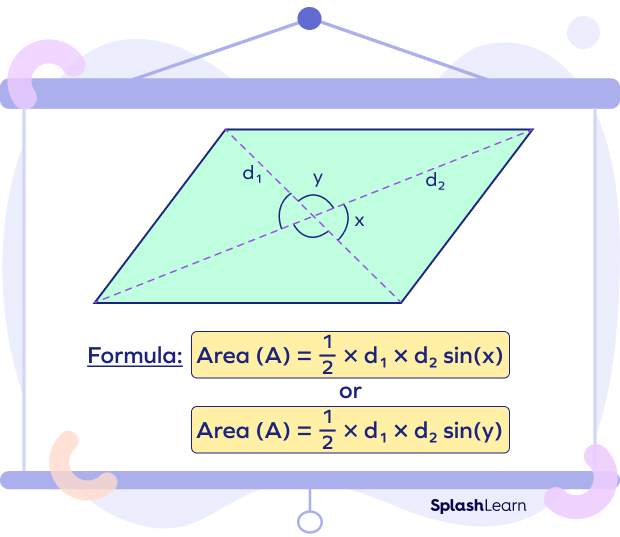
To calculate the area of a parallelogram using the lengths of its diagonals, you can use the following two formulas:

Area = $\frac{1}{2} \times d_{1} \times d_{2} \times sin(x)$ 

Area = $\frac{1}{2} \times d_{1} \times d_{2} \times sin(y)$

where:

• d₁ and d₂ are the lengths of the diagonals of the parallelogram.
• x or y is the angle of intersection between the diagonals.

Example: In a parallelogram, the lengths of the diagonals are 6 units and 8 units, and the angle between the diagonals is 90 degrees. Find the area of the parallelogram.

d₁= 6 units, d₂ = 8 units, x = 90 degrees

Using the formula for the area of a parallelogram with the lengths of its diagonals:

Area = $\frac{1}{2} \times d_{1} \times d_{2} \times sin(x)$

Area = $\frac{1}{2} \times 6 \times 8 \times sin(90)$

Area $= \frac{1}{2} \times 6 \times 81 = 24$ square units

Therefore, the area of the parallelogram is 24 square units

Area of Parallelogram: List of Formulas

Formulas to Calculate Area of a Parallelogram
Using Base and Height	A = b × h
Using Sides	A = a × b × sin(x)
Using Diagonals	A = $\frac{1}{2}$ × d1 × d2 × sin(y)

Facts about Area of a Parallelogram

Conclusion

In this article, we have learned about the area of parallelogram.the area of a parallelogram is necessary for measurements, real-world applications, problem-solving, understanding geometric relationships, and as a stepping stone for further mathematical and professional pursuits. Let’s solve some examples and practice problems to understand the concept better.

Solved Examples on the Area of Parallelogram

Example 1: A field has the shape of a parallelogram. The length of one side is 10 yards, and the corresponding height is 6 yards. Find the area of the field.

Solution: 

One side of the parallelogram = 10 yards 

Corresponding height = 6 yards

Area of a parallelogram = A = base $\times$ height.

Area = 10 yards $\times$ 6 yards = 60 square yards.

Therefore, the area of the field is 60 square yards.

Example 2: Calculate the area of a parallelogram whose diagonals are 15 units and 20 units, and the angle of intersection between the diagonals is 30°.

Solution:

Let d₁ = 15 units and d₂= 20 units.

Using the formula for the area of a parallelogram with the lengths of its diagonals:

Area = $\frac{1}{2} \times d_{1} \times d_{2} \times sin(x)$ 

Area = $\frac{1}{2} \times 15 \times 20 \times sin$(30°) 

Area = $\frac{1}{2} \times 15 \times 20 \times \frac{1}{2}$1 

Area = $15 \times 5$

Area = 75 square units

Therefore, the area of the parallelogram is 75 square units.

Example 3: Find the area of a parallelogram when two parallel sides are 40 units and 20 units respectively and the angle between them is 60.

Solution: 

Length of First Side = 40 units

Length of Second Side = 20 units

Angle between Both Sides = 60°

Using the Area of Parallelogram Formula, 

Area = a $\times$ b $\times$ sin(θ)

Area of Parallelogram = 40 $\times$ 20 $\times$ sin(60°)

Area of Parallelogram = 800 $\times$ sin(60°) 

Area of Parallelogram = 800 $\times$ 0.866

Area of Parallelogram = 692.8 square units.

Thus, the area of the parallelogram is 692.8 square units.

Practice Problems on the Area of Parallelogram

Frequently Asked Questions on the Area of Parallelogram