Base Area of a Triangular Prism – Definition, Formulas, Examples

What Is the Base Area of a Triangular Prism?

The area of the triangle located at the base of a triangular prism is referred to as the base area of a triangular prism. It is measured in square units.

A triangular prism is a polyhedron. It has three rectangular sides (lateral faces) and two triangular faces (one is the base and the other is the top). The two triangular faces are parallel and congruent. The base area of a triangular prism is the area of the base triangle.

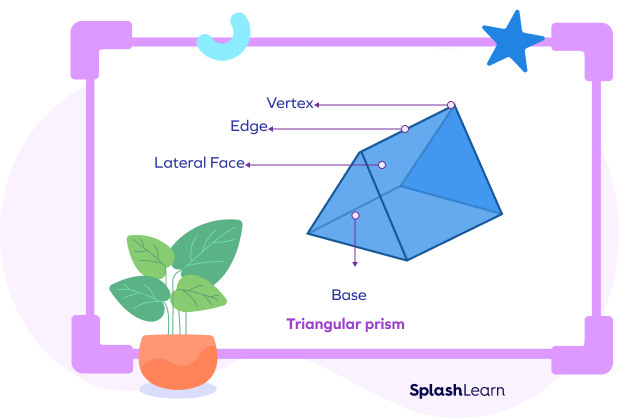
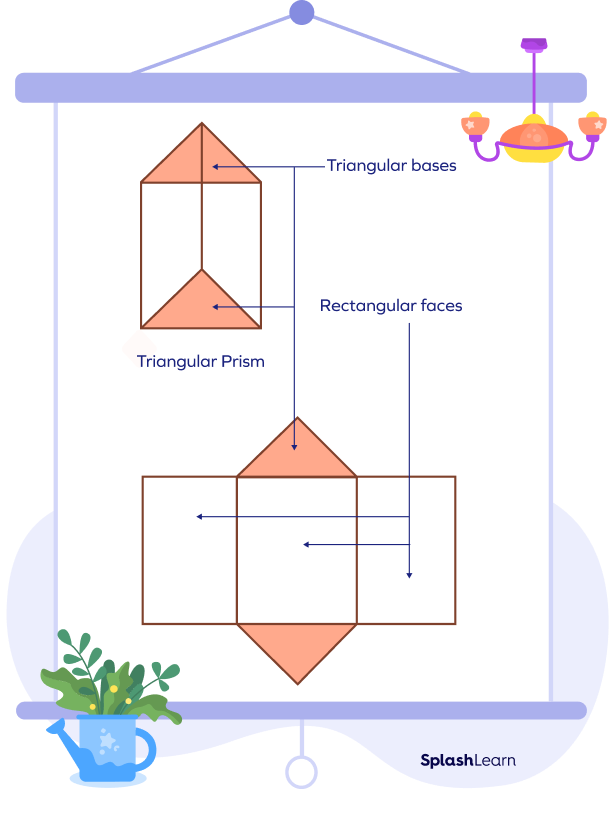
Take a look at the net of a triangular prism, which clearly shows the three rectangular lateral faces and two triangular bases.

Base Area of a Triangular Prism Formulas

To find the base area of a triangular prism, we must know different formulas for finding the area of a triangle. Let’s discuss some important formulas that can be helpful in finding the base area of a triangular prism.

Base Area of a Triangular Prism Formula When the Lengths of Sides of the Triangle Are Given

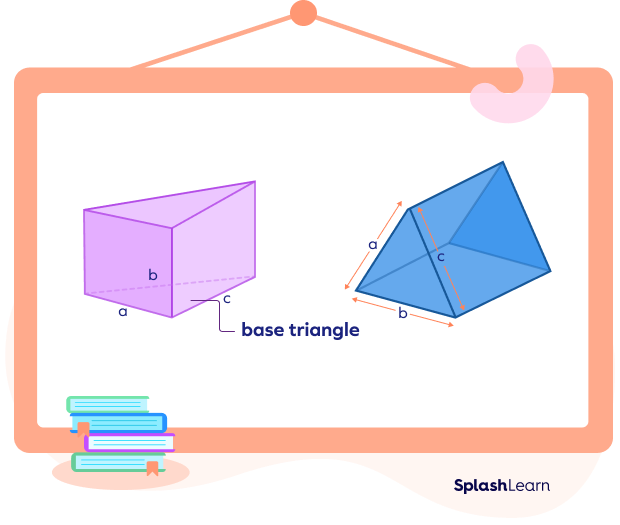
If the length of the sides of a triangular prism’s base is known, then its base area can be determined by using Heron’s formula.

Base area of a triangular prism = Area of the base triangle = A

$A = \sqrt{s(s – a)(s – b)(s – c)}$

where 

a, b, and c are the lengths of the sides of the base triangle, and

s = semiperimeter $= \frac{a + b + c}{2}$.

Base Area of a Triangular Prism Formula When the Base and Height of the Triangle Are Given

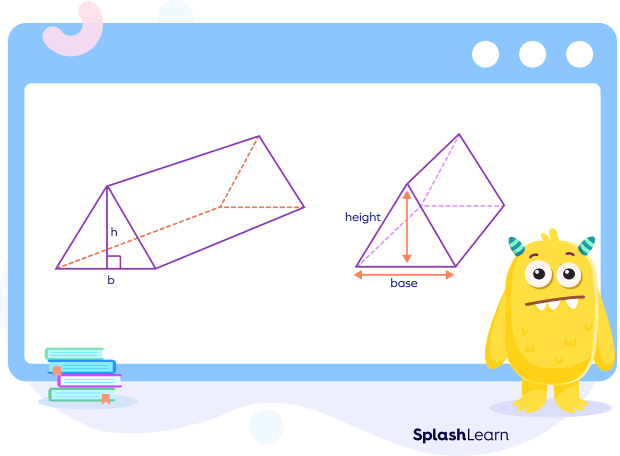
If the length of the base triangle and its height is known, then the base area of a triangular prism can be calculated as follows: 

Base area of a triangular prism = Area of the triangular base

If the base “b” and height “h” of the base triangle is given, then the base area of the triangular prism $= \frac{1}{2} \times b \times h$.

Let’s summarize!

Triangular Prism Base Area Formulas
What do we know about the base triangle?	Formula
Equilateral Triangle	$A = \frac{\sqrt{3}}{4} \times a^{2}$
Base = b, Height = h	$A = \frac{1}{2} \times b \times h$
Side-lengths: a, b, c, and semiperimeter s	$A = \sqrt{s(s – a)(s – b)(s – c)}$

How to Calculate the Base Area of a Triangular Prism

We can determine the base area of a triangular prism by finding the area of the base triangle. Depending on the known parameters and type of triangle in the base, various formulas can be used to determine the area of the base of a triangular prism. 

Let’s see how to calculate the base area of a triangular prism. 

Equilateral Triangle

If the base triangle is an equilateral triangle and each side length is “a,” then the base area of the triangular prism is given by 

$Area = \frac{\sqrt{3}}{4} \times a^{2}$

Triangle with base b and height h

If the base “b” and height “h” of the base triangle are given, then the base area of the triangular prism can be calculated as 

$A = \frac{1}{2} \times b \times h$.

Facts about the Base Area of a Triangular Prism

Conclusion

In this article, we have learned about the base area of a triangular prism for the different types of triangular bases. We discussed important formulas for finding the base area of a triangular prism. Let’s use these formulas to solve a few examples and practice problems.

Solved Examples on Base Area of a Triangular Prism

1. What is the base area of a triangular prism if the right triangle at its base has the base = 3 units and height = 4 units?

Solution:

The base of the given triangular prism is a right triangle whose base is 3 units and height 4 units.

Area of triangle with base b and height $h = \frac{1}{2} \times b \times h$

Base area of triangular prism $= \frac{1}{2} \times 3 \times 4$

Base area of triangular prism = 6 square units

2. Find the base area of the triangular prism whose sides are 3 inches, 4 inches, and 5 inches respectively.

Solution:

a = 3 inches, b = 4 inches and c = 5 inches

Using the Heron’s formula, we write

Area of triangle $= \sqrt{s(s – a)(s – b)(s – c)}$

Semiperimeter $(s) = \frac{a + b + c}{2} = \frac{3 + 4 + 5}{2} = \frac{12}{2} = 6$ inches

Substituting the values of s, a, b, and c in the above formula, we get

Area of triangle $= \sqrt{6(6 – 3)(6 – 4)(6 – 5)}$

Area of triangle $= \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{6 \times 6} = 6$ square inches

3. If the height of the triangular base of a triangular prism is 5 inches and the base length is 12 inches, find the base area of the triangular prism.

Solution: 

h = 5 inches and b = 12 inches

Area of the triangle when height and base side are given $= \frac{1}{2} \times b \times h$

∴ Area of triangle $= \frac{1}{2} \times 12 \times 5 = 30$ square inches

Base area = 30 square inches

4. If the base area of a triangular prism is $180 \;inch^{2}$ and the base length is 9 inches, then find the height of the triangular base.

Solution: 

The base area of a triangular prism=180 inch2 and b=9 inches

The base area of a triangular prism $= \frac{1}{2} \times b \times h$

$\Rightarrow \frac{1}{2} \times 9 \times h = 180$

$\Rightarrow h = \frac{180 \times 2}{9} = 40$ inches

Hence, the height of the triangular bases is 40 inches.

5. If the base of a triangular prism is an equilateral triangle and the perimeter of the base is 120 feet, find the base area of the prism.

Solution: 

Let the side of equilateral triangle $= a$

Perimeter $= 120$ feet

$\Rightarrow a + a + a = 120$

$\Rightarrow a = 40$ feet

Area of triangle $= \frac{\sqrt{3} a^{2}}{4}$

Area of triangle $= \frac{\sqrt{3}}{4} \times 40 \times 40 = 400\sqrt{3}$ square feet

6. The base sides of a triangular prism are in the ratio 7 : 5 : 10 and its perimeter is 22 units. Find the base area of the triangular prism.

Solution:

Let the sides be 7x, 5x, and 10x.

Perimeter $= 7x + 5x + 10x = 22$

$\Rightarrow 22x = 22$

$\Rightarrow x = 1$

Therefore, we get the values

a = 7 , b = 5, c = 10

$s = \frac{a + b + c}{2} = \frac{22}{2} = 11$ inches

∴  Area of triangle $= \sqrt{11(11 – 7)(11 – 5)(11 – 10)}$

∴  Area of triangle $= \sqrt{11 \times 4 \times 6 \times 1}$

∴  Area of triangle $= 2\sqrt{66}$ square units

Practice Problems on Base Area of a Triangular Prism

Frequently Asked Questions about Base Area of a Triangular Prism