What Is Binary Multiplication?
Binary multiplication is a fundamental operation on binary numbers which is quite similar to decimal multiplication. The multiplication of binary numbers can be calculated using the binary multiplication rules.
What is the Binary Number System?
A binary number system is the base-2 number system. It uses only two digits, 0 and 1 to form all the numbers. Each digit in the binary number system is said to be a bit.
If you understand the multiplication rules for the four combinations within 0 and 1, the binary multiplication becomes simple and straightforward. Let’s understand the binary multiplication rules.
Recommended Games
Rules of Binary Multiplication
Just like decimal multiplication, we define a multiplier and a multiplicand in the binary multiplication. The result of multiplication is called a product.
Binary Multiplication Rules:
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
Recommended Worksheets
Binary Multiplication Table
We can create a binary multiplication table using the rules mentioned above like this:
| × | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
We can also summarize the rules in the binary multiplication table as:
| Multiplicand | Multiplier | Product |
|---|---|---|
| 0 | 0 | 0 × 0 = 0 |
| 0 | 1 | 0 × 1 = 0 |
| 1 | 0 | 1 × 0 = 0 |
| 1 | 1 | 1 × 1 = 1 |
Note:
When we perform binary multiplication, we need to add the partial products just like decimal multiplication. Take a look at the binary addition rules that will be helpful.
Binary Addition Rules:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (carry 1)
How to Perform Binary Multiplication
Let’s understand the binary multiplication with steps. Consider the following example.
Binary multiplication example: Multiply 10102 and 10112.
The rules for binary multiplication are as follows:
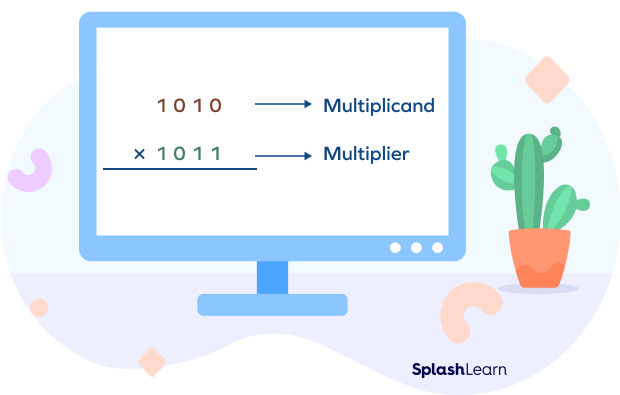
Step 1: Write down the multiplicand and multiplier one below each other (such that the place values are aligned properly). Write the multiplication sign (×) as we do in the decimal column multiplication method.
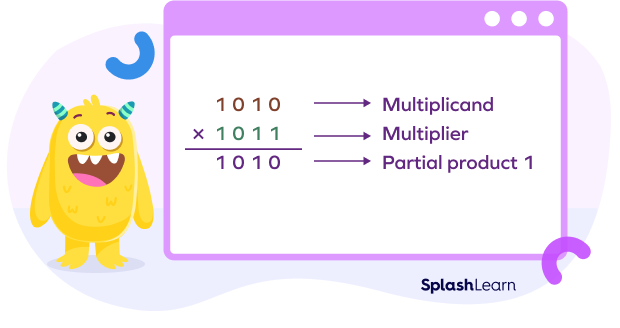
Step 2: Multiply the rightmost digit (Ones digit) or the least significant bit (LSB) of the multiplier (second number) with all the digits of the multiplicand (first number).
Here, we will multiply all the digits of (1010)2 with the rightmost digit of 10112, which is 1. We call the result as the partial product.
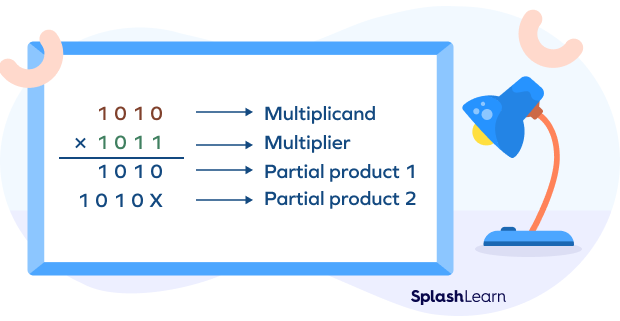
Step 3: In the next row, add a placeholder of ‘0’ or ‘X’ at the first position. Multiply all the digits of the multiplicand by the second digit (digit at the Two’s place).
Step 3: Repeat the same process until we reach the most significant bit (MSB) which is the left-most digit of the multiplicand. Make sure that we have multiplied each digit of the multiplier with all the digits of the multiplicand.
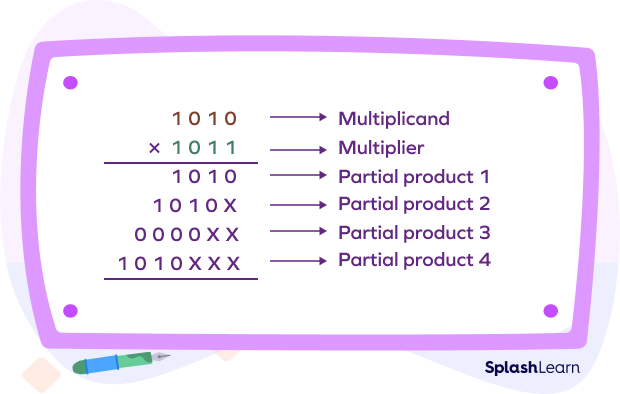
Step 5: Finally, add all the partial products. To add all the binary numbers use the rules of binary addition.
Example 2: Find the product of 10012 and 1012.
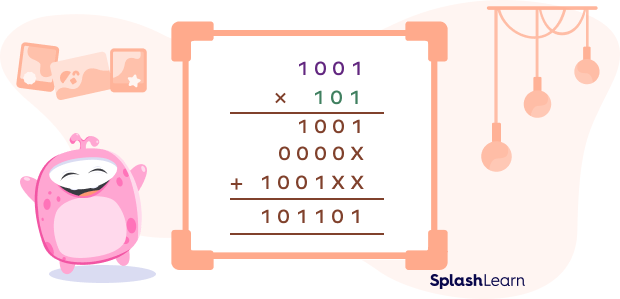
Facts about Binary Multiplication
- You can always verify the answer to the binary multiplication by converting the whole problem into the decimal number system.
Conclusion
In this article, we learned about binary multiplication, rules for binary multiplication, and the step-by-step instructions to multiply two binary numbers. Let’s use the rules and steps we learned to solve a few examples and practice problems.
Solved Examples on Binary Multiplication
1. Multiply (101)2 by (11)2.
Verify your answer.
Solution:
(101)2 × (11)2 = (01111)2

(101)2 = 510
(11)2 = 310
Product = 5 × 3 = 15
1510 = 11112
2. Find the product of (110)2 by (100)2.
Solution:
Let’s multiply (110)2 by (100)2.
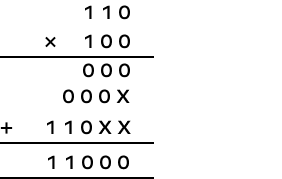
(110)2 × (100)2 = (11000)2
Decimal value: 6 × 4 = 24
3. What is the product of (1101)2 by (111)2?
Solution:
Let’s multiply (1101)2 by (111)2.
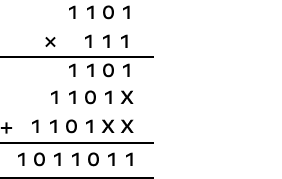
(1101)2 × (111)2 = (01011011)2
Decimal value: 13 × 7 = 91
Practice Problems on Binary Multiplication
Binary Multiplication - Rules, Types, Steps, Examples, FAQs
In the binary decimal number system, the product of 0 and 0 is ____.
0 × 0 = 0
What is the product of 1 and 1 in binary multiplication?
1 × 1 = 1
Using binary multiplication rules, find $(111)_{2}$ by $(10)_{2}$.
$111_{2} \times 10_{2} = 1110_{2}$
The product of $(1001)_{2}$ by $(111)_{2}$ is ____.
$(1001)_{2} \times (111)_{2} = (0111111)_{2}$
Frequently Asked Questions on Binary Multiplication
What is the 1’s complement of a binary number?
The 1’s complement of a binary number is the binary number obtained by interchanging 0 and 1.
1’s complement of 111 is 000.
1’s complement of 10101 is 010101.
How does binary multiplication work?
Binary multiplication is like traditional multiplication, but with only two digits (0 and 1). Multiply binary numbers digit by digit, carrying over like in decimal. Add up shifted products to get the result.
What are binary multiplication rules?
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1




































