Fractions in Lowest Terms: Definition with Examples

What Are Fractions in Lowest Terms?

A fraction is said to be in lowest terms if the numerator and denominator have no common factors other than 1. A fraction in lowest terms is also termed as a fraction in the simplest form. 

Consider an example: Suppose Oliver ate 3 out of 6 slices of a pizza. That means he had $\frac{3}{6}$ fraction of the pizza. Let’s visualize this. Take a look at the portion of the pizza he had.

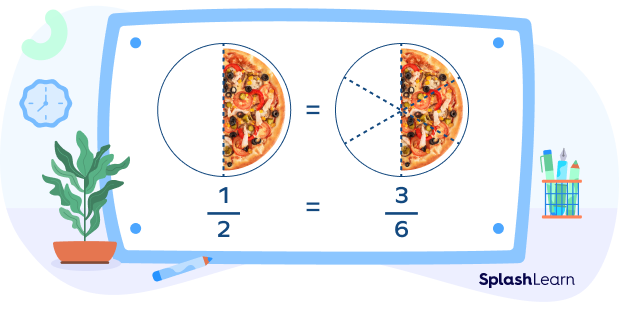
However, it looks like Oliver had a $\frac{1}{2}$ pizza. How come the fractions $\frac{3}{6}$ and $\frac{1}{2}$ represent the same value? 

$\frac{3}{6}$ and $\frac{1}{2}$ have the same value because $\frac{1}{2}$ is the lowest form of $\frac{3}{6}$. 

$\frac{3}{6}$ simplified gives $\frac{1}{2}$. In other words, we say that these are equivalent fractions.

Fractions in the Lowest Term Definition

A fraction is said to be in lowest terms if the GCD of the numerator and denominator is 1.

Example: $\frac{7}{8}$ is a fraction in lowest terms since GCD(7,8) $= 1$

However, $\frac{6}{8}$ is not in its lowest terms since GCD(6,8) $= 2$

You might wonder what is $\frac{1}{2}$ in lowest terms? What is $\frac{1}{2}$ simplified?

The answer is straightforward! $\frac{1}{2}$ itself is in the simplified form.

How to Reduce Fractions in Lowest Terms

Reducing fractions to lowest terms refers to simplifying the fractions such that the numerator and denominator become coprime (relatively prime).

In other words, reducing fractions to lowest terms in math means to reducing fractions to a form $\frac{a}{b}(b \neq 0)$ such that GCD(a,b) $= 1$.

Let’s learn two simple ways to reduce the fractions in lowest terms.

Dividing by Common Factors

Step 1: Divide both numerator and denominator by their lowest common factor (or any common factor). 

Step 2: Repeat this step for the resulting fraction.

Step 3: Continue this process until the only common factor is 1. 

This method is simple but time-consuming. It uses several steps to get to the answer.

Example 1: Reduce $\frac{48}{60}$ in lowest terms. 

$\frac{48 \div 2}{60 \div 2} = \frac{24}{30}$ …2 is the common factor of 48 and 60.

$\frac{24 \div 2}{30 \div 2} = \frac{12}{15}$ …2 is the common factor of 24 and 30.

$\frac{12 \div 3}{15 \div 3} = \frac{4}{5}$ …3 is the common factor of 48 and 60.

4 and 5 have no common factors other than 1.

4860 in its simplest form is 45.

Example 2: Write each fraction in lowest terms.

i) $\frac{6}{8}$ in lowest terms $= \frac{6 \div 2}{8 \div 2} = \frac{3}{4}$

ii) $\frac{135}{180}$ simplified $= \frac{135 \div 45}{180\div45} = \frac{3}{4}$

Using the Greatest Common Divisor

Here, we divide the numerator and the denominator by the greatest common factor. The greatest common factor (GCF) method of reducing fractions involves only two simple steps.

Step 1: Find the GCD of the numerator and the denominator.

Step 2: Divide both the numerator and the denominator by the GCD.

Example 1: $\frac{48}{60}$

Let’s first find the GCD of 48 and 60.

$48 = 2 \times 2 \times 2 \times 2 \times 3$

$60 = 2 \times 2 \times 3 \times 5$

GCD(48, 60) $= 2 \times 2 \times 3 = 12$

Dividing both numerator and denominator by GCD, we get

$\frac{48 \div 12}{60 \div 12} = \frac{4}{5}$

Example 2: $\frac{16}{50}$

$16 = 2 \times 2 \times 2 \times 2$ 

$50 = 2 \times 5 \times 5$

GCD(16, 50) $= 2$

$\frac{16 \div 2}{50 \div 2} = \frac{8}{25}$

Reducing Algebraic Fractions to Lowest Terms

Lowest terms in algebra refers to simplifying a fraction with polynomials as numerator and denominator to its lowest form.

Step 1: Factorize polynomials in the numerator and denominator.

Step 2: Cancel out the common factors.

Step 3: Simplify.

SImplify $\frac{x^2\;-\; 5x + 6}{x^2\;-\;9}$:

Factorize the expressions given in numerator and denominator. $x^2\;-\;5x + 6 = x^2\;-\;2x\;-\;3x + 6$

$= x (x\;-\;2)\;-\;3(x\;-\;2)$

$= (x\;-\;2)(x\;-\;3)$

and 

$x^2\;-\;9 = (x\;-\;3)(x + 3)$

Cancel the common terms.

$\frac{x^2\;-\; 5x + 6}{x^2\;-\;9} = \frac{(x\;-\;2)(x\;-\;3)}{(x\;-\;3)(x + 3)} = \frac{(x\;-\;2)}{(x + 3)}$

Solved Examples on Fractions in Lowest Terms

1. Express $\frac{121}{187}$ in lowest terms.

Solution: 

$121 = 11\times11$

$187 = 11\times17$

GCD$(121,\; 187) = 11$

$\frac{121\div 11}{187 \div11} = \frac{11}{17}$

2. Simplify and write $\frac{96}{108}$ in lowest terms.

Solution:

$96 = 2\times2\times2\times2\times2\times3$

$108= 2\times2\times3\times3\times3$

GCD$(96,\;108) = 2\times2\times3 = 12$

$\frac{96 \div12}{108 \div12} = \frac{8}{9}$

Thus, $\frac{96}{108} = \frac{8}{9}$

3. Express $\frac{x^2 + 4x + 4}{x^2\;-\;4}$ in lowest terms.

Solution:

Using identities:

$(a + b)^2 = a^2 + 2ab + b^2$ 

$a^2\;-\;b^2 = (a + b)(a\;-\;b))$

$\frac{x^2 + 4x + 4}{x^2\;-\;4} = \frac{x^2 + (2\times2\times x) + 2^2}{x^2\;-\;2^2} = \frac{(x + 2)(x + 2)}{(x + 2)(x\;-\;2)} = \frac{x + 2}{x \;-\; 2}$

4. Reduce to lowest terms: $\frac{180}{354}$

Solution: 

$180 = 2\times2\times3\times3\times5$

$354 = 2\times3\times59$

GCD$(180,\; 354) = 2\times3 = 6$

$\frac{180\div 6}{354 \div 6} = \frac{30}{59}$

5. Express $\frac{105}{945}$ in lowest terms. 

Solution:

$105 = 3\times5\times7$

$945 = 3\times3\times3\times5\times7$

GCD$(180,\; 354) = 3\times5\times7 = 105$

$\frac{105\div 105}{945 \div 105} = \frac{1}{9}$

6. What is the lowest term of $\frac{4}{8}$?

Solution:

GCD$(4,\; 8) = 2$

Dividing both numerator and denominator by 2, we get

$\frac{4}{8} = \frac{4 \div2}{8 \div2} = \frac{1}{2}$

The fraction $\frac{4}{8}$ in its lowest term is $\frac{1}{2}$. 

7. Is $\frac{3}{4}$  in the lowest terms?

Solution:

Here, 3 and 4 are coprime numbers.

GCD$(3,\; 4) = 1$

Thus, $\frac{3}{4}$ is in lowest terms.

Practice Problems on Fractions in Lowest Terms

Frequently Asked Questions on Fractions in Lowest Terms