Simplest Form – Definition, Methods, Facts, Examples, FAQs

What Is the Simplest Form?

In mathematics, the simplest form refers to the most reduced or simplified representation of a fraction. It is when the numerator and denominator have no common factors other than 1. 

A fraction written in the simplest form cannot be further reduced. On reducing the fraction into simplest form, the value of the fraction remains the same.

Example: The fraction $\frac{8}{12}$ is not in simplest form because both 8 and 12 can be divided by 4. By dividing both the numerator and denominator by 4, we get the simplified fraction $\frac{2}{3}$, which is in its simplest form.

Simplifying fractions to their simplest form makes them easier to work with and compare. It provides a clear and concise representation of the relationship between the numerator and denominator.

We can further say that the simplified fraction and the actual fraction are equivalent fractions. 

Example: 

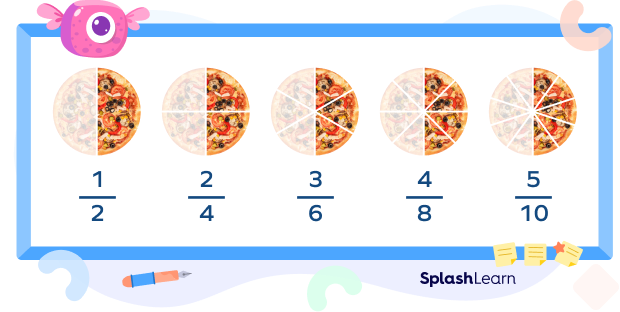
Simplest form of $\frac{4}{8}$ is $\frac{1}{2}$. 

Simplest form of $\frac{2}{4}$ is $\frac{1}{2}$.

Simplest form of $\frac{3}{6}$ is $\frac{1}{2}$.

Simplest form of $\frac{5}{10}$ is $\frac{1}{2}$.

All these fractions are equivalent fractions and $\frac{1}{2}$ is the smallest equivalent fraction among them!

Fractions in the Simplest Form: Definition

A fraction is said to be in its simplest form if the greatest common factor (GCF) of its numerator and denominator is 1. 

A fraction is in its simplest form when the numerator and the denominator have no common factors besides one.

Examples and Non-examples of Fractions in Simplest Form

Fractions in their simplest form	Fractions NOT in their simplest form
$\frac{2}{7}$	$\frac{20}{70}$
$\frac{1}{9}$	$\frac{5}{45}$
$\frac{23}{9}$	$\frac{46}{18}$

How to Reduce Fractions to their Simplest Form

We can simplify the fractions by two methods. Let’s check them out.

Method 1 : Repeated division by Common Factors

Try to divide both the numerator and denominator by their common factors, until we cannot go any further. This method is a little bit tedious.

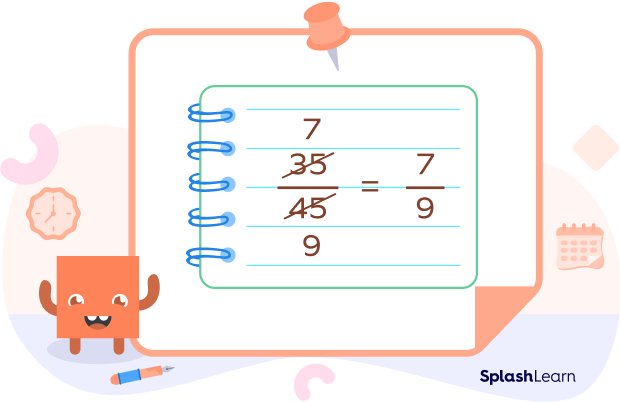
Example: $\frac{35}{105}$.

Factors of 35 = 1, 5, 7, and 35

Factors of 105 = 1, 3, 5, 7, 15, 21, 35 and 105.

Common factors of 35 and 105 = 1, 5, 7, and 35

Divide both the numerator and denominator by 5. 

$\frac{35}{105} = \frac{35 \div 5}{105 \div 5} = \frac{7}{21}$

Now, divide by 7. 

$\frac{7}{21} = \frac{7 \div 7}{21 \div 7} = \frac{1}{3}$

We cannot divide further since the common factor of 1 and 3 is 1.

So, the simplest form of $\frac{35}{105}$ is $\frac{1}{3}$.

Method 2: GCD Method

Divide both the numerator and denominator by their Greatest Common Divisor (GCD) or GCF. 

Example: Reduce $\frac{98}{126}$ into the simplest form. 

Step 1: Find the GCF of the numerator and the denominator. 

Factors of 98: 1, 2, 7, 14, 49 and 98.

Factors of 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63 and 126

Common factors of 98 and 126: 1, 2, 7, 14

GCF of 98 and 126 is 14. 

Step 2: Divide the numerator and denominator by the G.C.F. The fraction obtained after dividing is in the simplest form. 

 $\frac{98}{126} = \frac{98 \div 14}{126 \div 14} = \frac{7}{9}$

Thus, $\frac{7}{9}$ is the simplest form of the fraction $\frac{98}{126}$.

How to Reduce Mixed Fractions in the Simplest Form

A mixed number or a mixed fraction is a combination of a whole number and a proper fraction. To simplify a mixed fraction, we simplify the fractional part only. Reduce the fraction portion to lowest terms by finding the GCD.

Example 1: Simplify $5\frac{2}{4}$.

GCD(2, 4) = 2

$\frac{2}{4} = \frac{2 \div 2}{4 \div 2} = \frac{1}{2}$

Thus, $5\frac{2}{4} = 5\frac{1}{2}$

Example 2: Simplify $3\frac{10}{15}$.

$\frac{10}{15} = \frac{10\div 5}{15 \div 5} = \frac{2}{3}$

Simplest Form of Fractions with Exponents

To reduce the fractions having numerators and denominators with exponents, we expand the expressions using exponents in the numerator and denominator. 

Example 1: $\frac{5^{6}}{5^{3}}$ 

We will express the numerator and denominator as the product of numbers and then cancel out the common numbers.

$\frac{5^{6}}{5^{3}} = \frac{5 \times 5 \times 5 \times 5 \times 5 \times 5}{5 \times 5 \times 5} = 125$

Example 2: $\frac{3^{5}}{6^{2}} = \frac{3 \times 3 \times 3 \times 3 \times 3}{6 \times 6} = \frac{243}{36} = \frac{27}{4}$

Simplest Form of Fractions with Variables

To reduce the fractions with variables into the simplest form, use the expanded form of each expression in the numerator and denominator. 

Example 1: Simplify \frac{x^{5}\;y^{6}}{x^{3}\;y^{2}}$

The first step is to express the numerator and denominator as the product of variables.

$\frac{x^{5}\;y^{6}}{x^{3}\;y^{2}} = \frac{x \times x \times x \times x \times x \times y \times y \times y \times y \times y \times y}{x \times x \times x \times y \times y}$

The next step is to cancel out the common variables and write what is left.

$\frac{x^{5}\;y^{6}}{x^{3}\;y^{2}} = \frac{x^{2}}{y^{4}}$

Note: When dividing indices with the same base, subtract the powers and get the direct answer.

$\frac{x^{m}}{x^{n}} = x^{m-n}$

Ratio in the Simplest Form

A ratio is the comparison of two quantities of the same kind represented in the form of a : b or $\frac{a}{b}$, where a and b are the whole numbers. 

For converting the ratio in the lowest form, we use the same GCD method.

Reduce 34 : 289 into simplest form.

GCD(34, 289) = 17

Thus, by dividing 34 and 289 by 17 we get the ratio 34:289 in the simplest form 2 : 17.

Facts about the Simplest Form of a Fraction

Solved Examples on the Simplest Form of a Fraction

1. Write as a fraction in the simplest form:

i) $\frac{4}{16}$ 

ii) $\frac{24}{60}$

iii) $\frac{10}{24}$

iv) $\frac{12}{20}$

Solution: 

i) Given fraction $= \frac{4}{16}$

GCD of 4 and 16 is 4. 

$\frac{4}{16} = \frac{4 \div 4}{16 \div 4} = \frac{1}{4}$

ii) Given fraction $= \frac{24}{60}$

GCD of 24 and 60 is 12. 

$\frac{24}{60} = \frac{24 \div 12}{60 \div 12} = \frac{2}{5}$

$\frac{24}{60}$ simplified is $\frac{2}{5}$.

iii) Given fraction $= \frac{10}{24}$

GCD of 10 and 24 is 2. 

$\frac{10}{24} = \frac{10 \div 2}{24 \div 2} = \frac{5}{12}$

 $\frac{10}{24}$ simplified is$\frac{5}{12}$.

iv) Given fraction $= \frac{12}{20}$

GCD of 12 and 20 is 4.

$\frac{12}{20} = \frac{12 \div 4}{20 \div 4} = \frac{3}{5}$

$\frac{12}{20}$ simplified is $\frac{3}{5}$.

2. What is the simplest form of 24:36?

Solution: 

GCD of 24 and 36 is 12. 

$\frac{24}{36} = \frac{24 \div 12}{36 \div 12} = \frac{2}{3}$

So, the simplest form of 24:36 is equal to 2:3.

3. Reduce the mixed fraction $5\frac{25}{75}$ in the simplest form. 

Solution: 

Focus on the fractional part $\frac{25}{75}$.

GCD of 25 and 75 = 25

$\frac{25}{75} = \frac{25 \div 25}{75 \div 25} = \frac{1}{3}$

Thus, $5\frac{25}{75} = 5\frac{1}{3}$

Practice Problems on the Simplest Form of a Fraction