What Is the Difference between a Cube and a Cuboid?
The major distinction between a cube and a cuboid is that a cube has six identical square faces, while a cuboid has six rectangular faces.
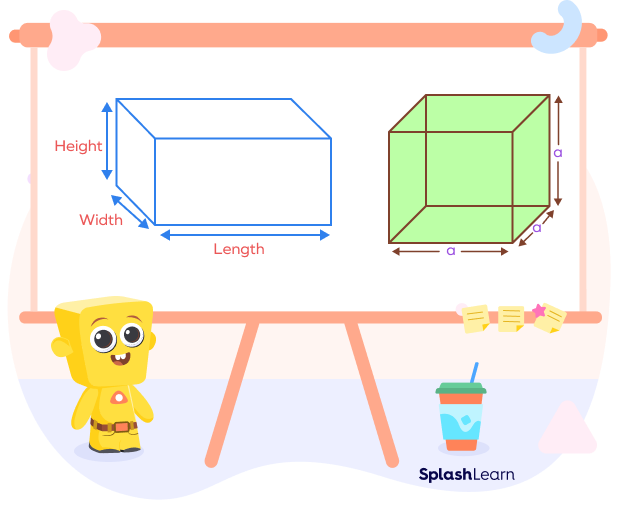
As you can see in the diagram below, the three dimensions: length, width, and height of a cube are the same (a), but that’s not the case with a cuboid.
Recommended Games
Definition of Cube
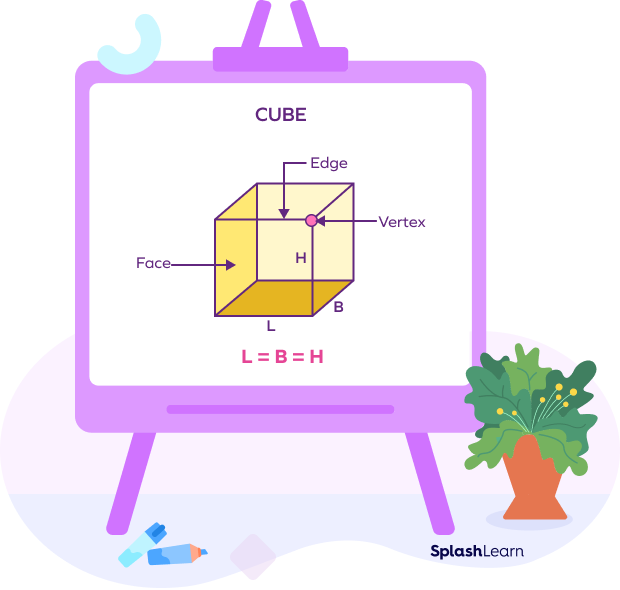
A cube is a three-dimensional shape with six identical square faces, 8 vertices, and 12 edges. It is a polyhedron. Two adjacent faces of a cube are at right angles to each other. A cube has the same length, width, and height since each face is a square. Each vertex of the cube meets three vertices and three faces.
Recommended Worksheets
Definition of Cuboid
A cuboid is a three-dimensional shape in which there are three pairs of rectangular faces that are opposite and identical. It has 6 quadrilateral faces, 12 edges, and 8 vertices.
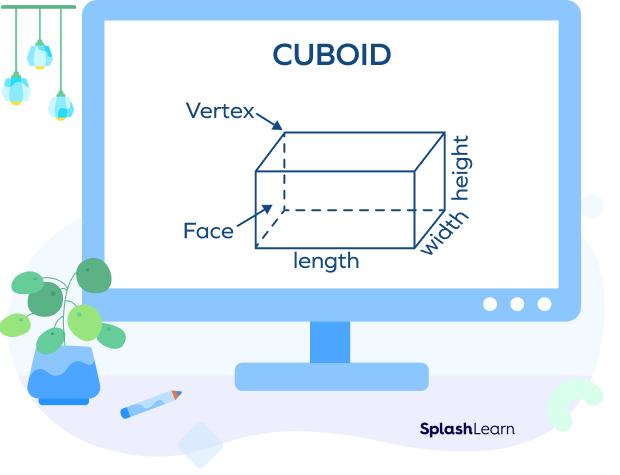
A cuboid is also known as a rectangular prism, rectangular box, rectangular parallelepipeds, and right prism.
Cube vs. Cuboid
| CUBE | CUBOID |
|---|---|
| Each face of a cube is a square. | Cuboids have rectangular faces. |
| All the edges of a cube are of equal measure. | All the edges of a cuboid are not of equal measure. |
| All the diagonals of a cube are equal. | All the diagonals are not equal in measurement. |
| All faces are congruent. | Opposite faces are congruent. |
| All edges have the same length. | Opposite edges have the same length. |
| It is a regular polyhedron. | It is not a regular polyhedron. |
| A cube is a three-dimensional form of a square. | A cuboid is a three-dimensional form of a rectangle. |
| Volume = (side)3 | Volume = length × breadth × height = lbh |
| Lateral Surface Area = 4 × (side)2 | Lateral Surface Area = 2(length + breadth) × height |
| Total Surface Area formula: 6 × (side)2 | Total Surface Area = 2 × (lb + bh + lh) |
 |  |
Facts about Difference between Cube and Cuboid
- A cube is a three-dimensional solid with all sides of equal length, forming six square faces, while a cuboid is also a three-dimensional solid with six rectangular faces, but its sides can have different lengths.
- Symmetry: A cube has a higher degree of symmetry than a cuboid due to its equal side lengths and identical faces.
- Diagonals: All the diagonals of the cube are equal but a cuboid has equal diagonals for only parallel sides.
Conclusion
In this article, we explored the fundamental distinctions between cubes and cuboids, understanding their unique properties and applications in geometry. Recognizing these differences aids in problem-solving and real-world context. Let’s apply our knowledge through solving examples and practicing MCQs for better comprehension.
Solved Examples on Difference Between Cube and Cuboid
1. Find the surface area of a cube given that its sides are equal to 7 units in length.
Solution:
Edge = 7 units
Surface area of cube = 6 ( edge)2
= 6×72
= 6 × 49
= 294 unit2
Hence, the surface area of the cube is 294 unit2.
2. Find the total surface area of the cuboid with dimensions length = 4 units, breadth = 3 units, and height = 7 units.
Solution:
Given length, breadth, and height = 4, 3, and 7 units, respectively.
Total Surface Area of cuboid = 2 (lb + bh + hl )
= 2 ( 6×5 + 5×9 + 9×6)
= 2 ( 30 + 45 + 54 )
= 2 x 129
= 258 unit2
So, the total surface area of this cuboid is 258 unit2.
3. Find out the volume of a cube if its edge is 7 units.
Solution:
Edge = a = 7 units
The volume of the cube is a3
V = a3
V = 73
V = 343 unit3
The volume of the cube will be 343 unit3.
4. The volume of a rectangular box is 523 unit³ and its base area is 210 unit². Find the height.
Solution:
Volume of the box = (l × b ×h) = 523 unit³
Base Area = (l × b) = 210 unit²
Therefore, the height of the room = (Volume)(Base Area)
h = 523210
h = 2.49 unit
So, the height of the room is 2.49 units.
5. What are the similarities between a cube and a cuboid?
Solution:
Both are 3D shapes.
Both have 6 faces.
Both have 12 edges.
Both have eight vertices.
Both are polyhedrons.
Both have 12 diagonals in total.
Practice Problems on the Difference between a Cube and a Cuboid
Difference between Cube and Cuboid - Definition, Examples, FAQs
What is the volume of the given cuboid?

Volume = 10 × 5 × 2 = 100 $feet^{3}$.
A cube has a volume of 125 cubic units. What is the length of each side?
V = $side^{3}$ = 125 cubic units
Thus, side = 5 units
The dimensions of a cuboid are l = 5 units, w = 4 units, and h = 3 units. What is its volume?
V= l × w × h = 5 × 4 × 3 = 60 $unit^{3}$.
Frequently Asked Questions on the Difference between a Cube and a Cuboid
Are squares and cubes the same shape?
No, a square is a two-dimensional shape, a quadrilateral with 4 equal sides. A cube is a three-dimensional shape whose each face is a square.
Is every cube a cuboid?
Yes. A cube is a special type of a cuboid, where all the dimensions, such as length, breadth and height, are equal. So, every cube is a cuboid.
What separates a cube from a cuboid is the main difference?
Cuboid and cube faces are primarily distinguished by their forms. A cube has a square face, while a cuboid has a rectangle face.
Are cubes and cuboids polyhedrons?
Yes, cubes and cuboids are polyhedrons because they are composed of polygons, such as squares and rectangles.




































